Aurélie 11/01/07
 

Agrégation 2005 : Structure cristalline hexagonale compact ; maille quadratique ; diffraction des RX

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

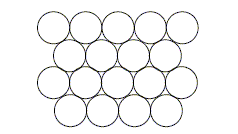
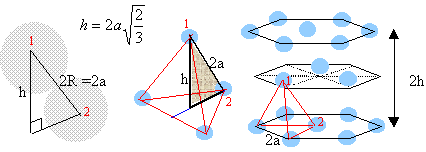
Le dioxyde de titane existe sous différentes variétés allotropiques. On se propose ici d'étudier la structure de la forme rutile. Sa structure dérive d'un empilement hexagonal quasi compact d'anions O2- dans lequel les cations occupent la moitié des sites octaédriques.

On considère pour l'instant une structure hexagonale compacte formée d'un seul type d'atomes considérés comme des sphères dures de rayon R.

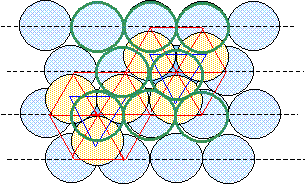
Compléter la figure afin de représenter le mode d'empilement des plans d'atomes successifs dans une telle structure hexagonale compacte.

Situer les sites tétraédriques et octaédriques sur cette figure.

site tétraèdrique
Maille conventionnelle de la structure hexagonale compacte :
Dessin de la maille conventionnelle ( 1/3 de la figure hexagonale ) que l'on utilise pour décrire une structure hexagonale dans le cas général.

Relations particulières vérifiées par les paramètres d'une telle maille

a=b ; c différe de a et de b

a=b=90° ; g= 120°.

1 noeud : sommet du parallélépipède construit à partir des vecteurs de base a, b, c. ( chaque sommet appartient à 8 mailles et compte pour 1/8)

Nombre d’atomes par maille : 2

chaque atome situé à un noeud appartient à 8 mailles et compte pour 1/8 ; l'atome central appartient en propre à la maille.

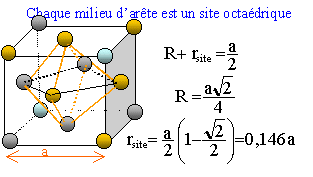
L'empilement hexagonal compact a la même compacité que la maille cubique faces centrées et les sites interstitiels sont de même nature. En utilisant cette analogie calcul de la taille d'un site octaédrique en fonction du rayon atomique R des atomes de l'empilement.

rsite = 0,146 a ; a = 4R/2½ d'où rsite = 0,414 R

Dans le cas du dioxyde de titane TiO2, montrons que la condition de stabilité de l'empilement est satisfaite à partir des rayons ioniques r(Ti4+ )=74 pm et r(O2-)=126 pm)

Les anions plus gros que les cations imposent le type de structure ; les cations occupent les sites laissés vacants.

La structure est stable si le rayon d'un cation, occupant un site, est supérieure à la taille du site.

rsite = 0,414 Ranion = 0,414*126 = 52 pm ; or r(Ti4+ )=74 pm , la condition de stabilité est vérifiée.

En réalité, la structure de TiO2 rutile est décrite dans une maille quadratique (a = b = 459,4 pm et c = 295,9 pm et les 3 angles sont droits) ; elle est donnée sur la figure ci-dessous :
atome
x/a
y/b
z/c
01
0,3
0,3
0
02
0,7
0,7
0
03
0,8
0,2
0,5
04
0,2
0,8
0,5
05
0,3
0,3
1
06
0,7
0,7
1

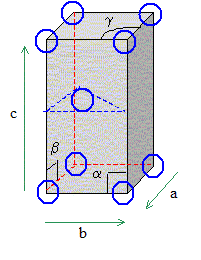
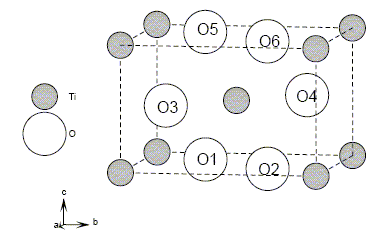
Détail de la structure cristalline de TiO2 rutile. Les atomes de titane sont situés aux sommets et au centre de la maille. Les coordonnées réduites (x/a,y/b,z/c) des atomes d'oxygène sont données dans le tableau.

Contenu de la maille :

Montrons que la répartition des atomes donnée par cette figure et par le tableau des coordonnées atomiques est bien en accord avec la formule TiO2.

Chaque cation situé à un sommet appartient 8 mailles et compte pour 1/8 ; le cation central appartient en propre à la maille : donc 2 cations par maille.

Les anions 01, 02, 05 et 06 appartiennent à 2 mailles et comptent pour 1/2 ; les anions 03 et 04 appartiennent en propre à la maille : donc 4 anions par mailles.

Cela correspond à la formule TiO2.

Masse volumique de TiO2 :

volume de la maille : V=a2c = (459,4 10-12)2* 295,9 10-12 =6,24 10-29 m3.

masse des 4 anions et des 2 cations par maille : m = 2 masse molaire TiO2/NA =2 (47,88 + 32) 10-3 / 6,02 1023 =2,65 10-25 kg

r= m/V =2,6510-25 /6,24 10-29 =4,25 103 kg m3.

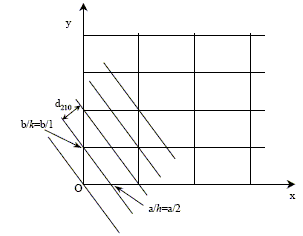
Pour déterminer les paramètres de maille d'un composé cristallisé, on utilise la technique de diffraction des rayons-X sur poudre. Dans un cristal, les plans réticulaires d'indice de Miller (hkl ) sont séparés d'une distance dhkl . La figure 4 donne une définition géométrique des indices de Miller qu'il n'est pas indispensable de connaître pour la suite.

Définition géométrique des indices de Miller. Pour plus de clarté, la figure donne la projectiondu réseau dans le plan (a, b). L'exemple donné correspond aux indices (2 1 0), c'est-à-dire que h=2 et k=1 et l=0. L'un des plans de cette famille coupe les axes en a/h = a/2, b/k = b/1 et est parallèle à c.

Dans le cas d'une symétrie quadratique, la distance inter-réticulaire pour la famille de plans (hkl ) est égale à :

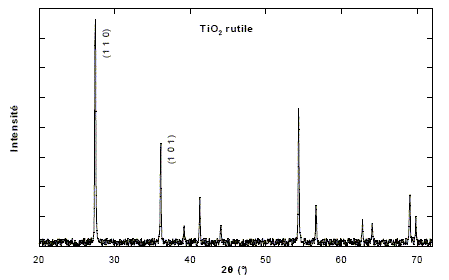
Tous les plans correspondant à la même distance inter-réticulaire contribuent à la raie de diffraction située à l'angle qhkl donné par la relation de Bragg :

2 dhkl sin qhkl= l.

Une poudre est formée d'un ensemble de petits cristaux orientés dans toutes les directions. C'est ainsi que toutes les familles de plans (hkl ) peuvent donner une raie de diffraction dans un diagramme de poudre.

Dans le cas de TiO2 rutile on obtient le diagramme ci-dessous (la longueur d'onde des rayons X utilisés est l = 154,06 pm).

diagramme de diffraction des rayons-X pour un échantillon de TiO2. L'abscisse est donnée en fonction de l'angle 2q, où q est l'angle de Bragg.

Les deux premières raies du diagramme de diffraction correspondent respectivement aux indices (1 1 0) et (1 0 1).

Calcul de dhkl :

h=k=1 ; l=0 ; a=459,4 pm et c =295,9 pm ;

d110 =[(h2+k2)/a2 + l2/c2]-½ = [(1+1)/459,42 ]-½ =459,4 / 2½ =324,84 pm

h=l=1 ; k=0 ; a=459,4 pm et c =295,9 pm ;

d101 =[(h2+k2)/a2 + l2/c2]-½ = [1/459,42 +1/295,92]-½ =248,76 pm

Angle de diffraction (2qhkl) pour ces deux raies : l = 154,06 pm

2 dhkl sin qhkl= l ; sin q110= 154,06 / (2*324,84) =0,237 ; q110=13,71 ° ; 2q110=27,43°

sin q101= 154,06 / (2*248,76) =0,310 ; q101=18,04 ° ; 2q101=36,08°

Le dioxyde de vanadium existe sous une forme allotropique isotype de TiO2 rutile. Cela signifie que les atomes occupent des positions très proches dans les deux structures. Par contre, la maille n'a pas exactement la même taille. Sur le diagramme de diffraction du dioxyde de vanadium, les deux premières raies sont situées en 2q 110 = 27,67° et 2 q 101 = 37,09°.

Paramètre de maille de cette variété de dioxyde de vanadium :

sin q 110 = sin(27,67 / 2 )= 0,2391

d110 = ½l/sin q 110 = 0,5*154,06 / 0,2391 = 322,13 pm

or d110 =[2/a2 ]-½ = a/2½ d'où a = 2½d110 =2½*322,13 = 455,56 pm.

sin q101= sin(37,09 / 2 )= 0,318.

d101 = ½l/sin q101 = 0,5*154,06 / 0,318 = 242,23 pm

or d101 =[1/a2 +1/c2]-½ =[1/a2 +1/c2] = 1/d2101 =1/242,232 =1,704 10-5.

1/c2=1,704 10-5-1/a2 = 1,704 10-5-1/455,562 = 1,222 10-5 ; 1/c= 3,496 10-3 ; c = 286,04 pm.

Evolution des paramètres de maille observée lorsque l'on passe de TiO2 à VO2 :

En se déplaçant dans une même période, on observe une contraction du nuage électronique et une diminution des rayons des ions isoélectroniques ; par suite une diminution des paramètres a, b, c de la maille.
retour -menu