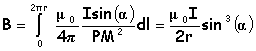Champ magnétique crée par une spire circulaire : dipole magnétique concours ITPE ( travaux publics) interne 2004

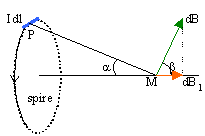
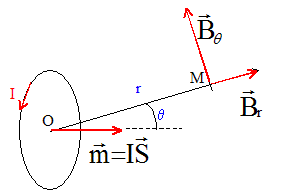
On considère une spire circulaire de centre O, de rayon r et d'axe z'z, parcourue par un courant permanent I

Champ magnétique B en tout point de l'axe z'z en un point M :

L'élément de courant Idl crée en M , le champ élémentaire dB, perpendiculaire à PM, de module :

Idl et PM étant perpendiculaire sin(q)=1

Par raison de symétrie le champ résultant sera porté par l'axe horizontal. La composante utile sera dBcos(b) = dBsin(a)

Pour tous les éléments Idl, l'angle a et PM sont les mêmes. L'intégration de dB sur toute la spire donne le module du champ résultant ( sin a = rayon r / PM )

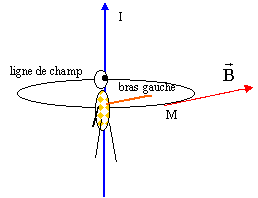
Le sens du champ magnétique est donné par la règle de l'observateur d'Ampère : le sens du champ est de la gauche vers la droite.

Que devient l'expression précédente lorsque r<<z ?

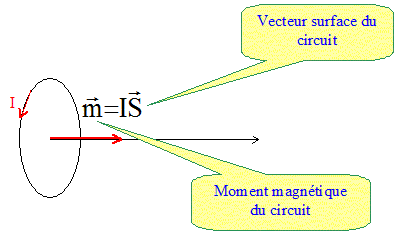
r/z <<1 et on peut confondre l'angle a, exprimé en radian, et sin a : sin a voisin de r/z

B= m₀I/(2r) * r³/z³ = m₀I / 2 * r²/z³

B = m₀I / (2p) * p r²/z³ ; S= p r², aire de la spire.

B= m₀/ (2p) m /z³ avec m = IS, moment magnétique du circuit.

Un dipôle magnétique est une distribution de courants localisés, de moment magnétique non nul ; les dimensions de la distribution de courant sont petites par rapport à de la distance à laquelle on étudie le champ ainsi créé.

Sachant que, en coordonnées sphériques, B_r = (m₀/(4p) 2 cos q m / r³

et B_q = (m₀/(4p) sin q m / r³.

si q =0 : z=r ; sin q =0 donc B_q =0 ; cos q = 1 donc B_r= m₀/ (2p) m /z³.

On retrouve l'expression B= m₀/ (2p) m /z³ du champ crée par une spire circulaire sur son axe, en un point éloigné.