|
Montage extracteur de racine carrée concours technicien laboratoire 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.
|
|
| .
. |
|
|
|
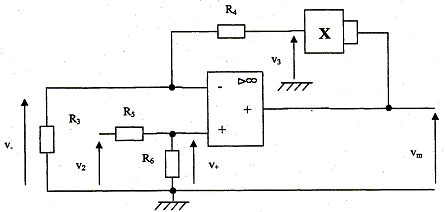
Exprimer v-(t) en fonction de v3(t), R3 et R4. réponse : v-(t) = R3 i soit i = v-(t) / R3 v-(t) = v3(t) + R4 i = v3(t) + R4 v-(t) / R3 v-(t) (1-R4 / R3 ) = v3(t) ; v-(t) (R3-R4 ) = R3 v3(t) v-(t) = R3 v3(t) / (R3-R4 ). Exprimer v+(t) en fonction de v2(t), R5 et R6. réponse : v+(t) = R6 i' soit i' = v+(t) / R6 v+(t) = v2(t) + R5 i' = v2(t) + R5 v+(t) / R6 v+(t) (1-R5 / R6 ) = v3(t) ; v+(t) (R6-R5 ) = R6 v2(t) v+(t) = R6 v2(t) / (R6-R5 ).
Exprimer v3(t) en fonction de vm(t) et k. réponse : v3(t) = kv2m(t). Exprimer vm(t) en fonction de v2(t), k et des résistances du montage. réponse : v3(t) = kv2m(t). v+(t) =v-(t) ; R6 v2(t) / (R6-R5 ) = R3 v3(t) / (R3-R4 ) v3(t) = R6 (R3-R4 ) v2(t) / [ (R6-R5 ) R3]. vm(t) = 1/k½ { R6 (R3-R4 ) v2(t) / [ (R6-R5 ) R3] }½.
Montrer que v2m(t) peut s'écrire : v2m(t) = 1/k a v2(t) où a est une constante que l'on explicitera. réponse : v2m(t) = 1/k R6 (R3-R4 ) / [ (R6-R5 ) R3] v2(t) a =R6 (R3-R4 ) / [ (R6-R5 ) R3]. A quelle condition sur les résistances a t-on vm(t) = [v2(t)/k]½ ? réponse : a doit être égal à 1. R6 (R3-R4 ) = (R6-R5 ) R3.
|
|
|
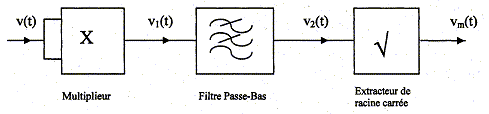
On rappelle que : v1(t) = kv2(t) ; v2(t) = <v1(t)> ; vm(t) = [v2(t)/k]½ ; k = 0,1 V-1. Montrer que vm(t) = [<v(t)>]½. réponse : vm(t) = [v2(t)/k]½ =[<v1(t)> / k]½=[<v2(t)>]½ vm(t) = [<v(t)>]½. On applique maintenant à l'entrée du montage une tension sinusoïdale v(t) = V cos (2pft) d'amplitude V= 10 V et de fréquence f= 50 Hz. Exprimer v1(t) en faisant apparaître sa composante continue et sa composante alternative. Que vaut la fréquence f1 de cette dernière ? réponse : v1(t) = kv2(t) = k V2cos (2pft) = ½ k V2[1 + cos (4pft) ] avec f1 = 2f = 100 Hz. Donner l'expression littérale approchée de v2(t) et sa valeur numérique approchée. réponse : v2(t) = <v1(t)> La valeur moyenne de la fonction cosinus est nulle. v2(t) =½ k V2. En déduire l'expression littérale approchée de vm(t) et sa valeur numérique approchée. Comparer à la valeur efficace Veff de v(t). réponse : vm(t) = [v2(t)/k]½ =[½V2]½= V/2½= Veff .
|
|
|
|
