Aurélie 10/05/07
 

concours ergo Berck indice de réfraction ; solénoïde ; associations de résistors ; dipole RL. 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Une lampe à vapeur de sodium émet une radiation de fréquence f = 5,1 1014 Hz.

La longueur d'onde de cette radiation dans un milieu transparent d'indice n est l = 400 nm. ( c = 3,0 108 m/s)

Calculer n ( 1,1 ; 1,3 ; 1,5 ; 1,7 ; 1,9 ; aucune réponse exacte)

On note v la célérité de l'onde dans le milieu : n = c/v soit v = c/n.

l = v/f ; d'où l = c / ( n f) ; n = c / (l f ) ;

n = 3 108 / ( 400 10-9 * 5,1 1014) =3 108 / (4*5,1 107) = 3/ 2,04 ; n = 1,5.

On considère un solénoïde de longueur L= 40 cm et comprenant N= 600 spires.

Au centre O du solénoïde on mesure la valeur B du champ magnétique.

Lorsque le solénoïde est parcouru par un courant d'intensité I1 = 270 mA, la valeur du chmp magnétique est B1 = 340 mT. On négligera le champ magnétique terrestre. m 0 = 4 p 10-7 S.I.

Calculer la valeur B2 du champ magnétique ( en mT) lorsque l'intensité vaut I2 = 450 mA. ( 0,20 ; 0,34 ; 0,57 ; 0,78 ; 0,87; aucune réponse exacte)

La valeur du champ magnétique est proportionnelle à l'intensité du courant.

B2 = B1*I2/I1 ;

B2 = 340 * 450 / 270 = 340*5/3 mT ou bien B2 = 0,34*5/3 mT

B2 = 0,57 mT.

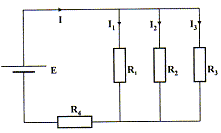
On considère le circuit ci-dessous composé d'un générateur idéal de tension continue de f.e.m E et de 4 conducteurs ohmiques.

R1 = 5 W ; R2 = 10 W ; R3 = 15 W ; R4 = 20 W.

L'intensité du courant dans le conducteur ohmique R3 vaut I3 = 40 mA.

Déterminer la valeur de E ( V). ( 4 ; 5 ; 6 ; 7 ; 8 ; aucune réponse exacte)

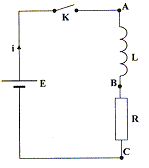
La tension aux bornes des conducteurs ohmiques montés en dérivation , R1, R2, R3 est la même et vaut :

R3I3 =15 * 0,04 = 0,6 V.

par suite I2 =0,6 /R2 =0,6/10 =; I2 = 0,06 A.

par suite I1 =0,6 /R1 =0,6/5 =; I1 = 0,12 A

Intensité dans la branche principale : I = I1 +I2 + I3 = 0,06+0,12+0,04 = 0,22 A.

La tension aux bornes du conducteur ohmique R4, traversé par l'intensité I, vaut R4I = 20*0,22 =4,4 V

Additivité des tensions : E = 0,6 + 4,4 ; E = 5,0 V.

On considère le circuit ci-dessous constitué d'un générateur idéal de tension continue, de f.e.m E, d'une bobine d'inductance L et de résistance négligeable, d'un conducteur ohmique de résistance R et d'un interrupteur K.

La date t=0 coïncide avec la fermeture de K.

L= 50 mH ; E =6,0 V R = 100 W.

Parmi les affirmations suivantes, combien y en a t-il d'exactes ?

- La tension aux bornes de la bobine est nulle à la date t=0. Faux.

A la fermeture de l'interrupteur, l'intensité est nulle : la tension aux bornes du résistor est donc nulle.

Additivité des tensions UL+UR= E ; Or UR=0 d'où UL=E.

- La constante de temps du circuit est t = 5 ms. Faux.

t = L/R = 0,05 / 100 = 5 10-4 s = 0,5 ms.

- La tension aux bornes de la résistance est égale à E lorsque le régime permanent est établi. Vrai.

En régime permanent dI/dt = 0 ; or la tension aux bornes de la bobine est UL= L dI/dt = 0.

Additivité des tensions UL+UR= E ; Or UL=0 d'où UR=E.

- L'intensité du courant en régime permanent est égale à 6 mA. Faux.

I = E/R = 6/100 = 0,06 A ; I = 60 mA.

- Lorsque le régime permanent est atteint, l'énergie magnétique emmagasinée dans la bobine vaut EM=90 mJ. Vrai.

EM = ½LI2 =0,5*0,05*0,062 =9 10-5 J ; EM=90 mJ

 
 

retour -menu