Aurélie 11/04/07
 

Concours Capes : étude magnétique du stator du moteur asynchrone 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

 

Etude magnétique du stator :

Les vecteurs sont écrits en gras et en bleu.

Soit un solénoïde circulaire, de longueur supposée quasi-infinie suivant son axe (Ox) parcouru par un courant d'intensité I. Le nombre de spires par unité de longueur est n. Le vecteur surface S = Sux est choisi grâce à la "règle de la main droite" à partir de l'orientation du courant I qui circule dans le solénoïde.

  1. Exprimer le champ magnétique B crée par un solénoïde en un point quelconque de l'espace en fonction de la perméabilité du vide m0, n, I et de ux.
  2. Le stator du moteur asynchrone est constitué de trois enroulements cylindriques ( qu'on assimilera à des solénoïdes infinis) identiques.

    On repère les axes respectifs des solénoïdes par les vecteurs :     u1 =ux ;
    u2     =cos (2p/3)ux +sin(2p/3)uy ; u3 =cos (2p/3)ux -sin(2p/3)uy.
    On alimente ces trois bobines grâce à un courant triphasé crée par un alternateur triphasé. Ainsi, chacune des intensités Ik(t) est de la forme :
    Ik(t) =-I0 sin(     wtri t+Yk) avec Y1=0 ; Y2=-2p/3 ; Y3=2p/3.
    - Montrer que les composantes du champ magnétique peuvent s'exprimer sous la forme : Bx(t) = -B0sin(     wtri t ) ; By(t) = B0 cos( wtri t ).
    - Montrer que le stator du moteur asynchrone crée en O un champ magnétique de valeur constante B0 tournant autour de l'axe (Oz) à la vitesse angulaire constante     WB = wB uz. Identifier wB.
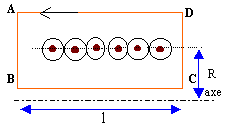
Champ du solénoïde :

Tout plan perpendiculaire à l'axe de la bobine est un plan de symétrie pour le courant : en conséquence, le champ magnétique est perpendiculaire à ce plan.

La distibution de courant étant invariante par rotation autour de l'axe de la bobine, et par translation sur cet axe, le champ est porté par l'axe de la bobine et ne dépend que de la distance à l'axe.

Le champ est nul à l'extérieur de la bobine, car les lignes de champ ne sortent pas du solénoïde.

Appliquons le théorème d'Ampère au contour ABCD

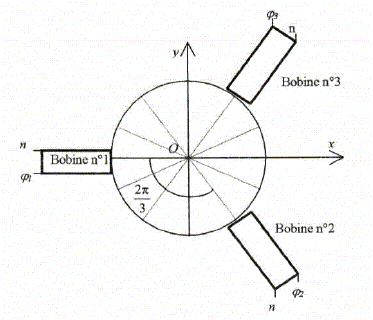
le champ étant perpendiculaire à AB et à CD, la circulation est nulle le long de AB et CD

le champ est nul à l'extérieur, la circulation du champ est nulle le long de AD

la circulation du champ est m0N I le long de BC

m0N I = B l

B= m0n I avec n= N/ l , nombre de spire par mètre.

le champ est uniforme et colinéaire à l'axe à l'intérieur du solénoïde.

 Composantes du champ magnétique :

Le champ total est la somme vectorielle des champs crées par chaque solénoïdes, le milieu étant linéaire.

B= -m0n I0 [sin( wtri t )u1+ sin( wtri t-2p/3 )u2 + sin( wtri t+2p/3 )u3 ]

u1 =ux ; u2 =cos (2p/3)ux +sin(2p/3)uy ; u3 =cos (2p/3)ux -sin(2p/3)uy.

B= -m0n I0 [sin( wtri t )ux+ sin( wtri t-2p/3 )(cos (2p/3)ux +sin(2p/3)uy ) + sin( wtri t+2p/3 )(cos (2p/3)ux -sin(2p/3)uy].

Bx(t) = -m0n I0 [sin( wtri t )+ sin( wtri t-2p/3 )(cos (2p/3)+ sin( wtri t+2p/3 )(cos (2p/3)]

Or sin( wtri t-2p/3 )(cos (2p/3) =½[sin(wtri t-4p/3 ) + sin( wtri t)]

Or sin( wtri t+2p/3 )(cos (2p/3) =½[sin(wtri t ) + sin( wtri t+4p/3)]

sin( wtri t-2p/3 )(cos (2p/3)+ sin( wtri t+2p/3 )(cos (2p/3) =sin(wtri t ) +½[sin(wtri t-4p/3 ) + sin( wtri t+4p/3)]

Or sin(wtri t-4p/3 ) = sin(wtri t) cos(4p/3 ) -cos(wtri t) sin(4p/3 )

Or sin(wtri t-+4p/3 ) = sin(wtri t) cos(4p/3 ) +cos(wtri t) sin(4p/3 )

½[sin(wtri t-4p/3 ) + sin( wtri t+4p/3)] = sin(wtri t) cos(4p/3 ) =-0,5 sin(wtri t).

sin( wtri t-2p/3 )(cos (2p/3)+ sin( wtri t+2p/3 )(cos (2p/3) =0,5sin(wtri t )

Bx(t) = -m0n I0 [sin( wtri t )+ sin( wtri t-2p/3 )(cos (2p/3)+ sin( wtri t+2p/3 )(cos (-2p/3)]

Bx(t) = -1,5m0n I0 sin( wtri t ) = -B0sin( wtri t ).

 
 

By(t) = -m0n I0 [sin( wtri t-2p/3 )(sin (2p/3)-sin( wtri t+2p/3 )(sin (2p/3)]

Or sin( wtri t-2p/3 )(sin (2p/3) =½[cos( (wtri t-4p/3) - cos( wtri t )]

Or sin( wtri t+2p/3 )(sin (2p/3)=½[cos( (wtri t) - cos( wtri t+4p/3 )]

sin( wtri t-2p/3 )(sin (2p/3)-sin( wtri t+2p/3 )(sin (2p/3) = - cos( wtri t )+½[cos( (wtri t-4p/3)+cos( wtri t+4p/3 )]

Or cos( (wtri t-4p/3) = cos(wtri t) cos(4p/3) + sin(wtri t) sin(4p/3)

Or cos( (wtri t+4p/3) = cos(wtri t) cos(4p/3) - sin(wtri t) sin(4p/3)

½[cos( (wtri t-4p/3)+cos( wtri t+4p/3 )] = cos(wtri t) cos(4p/3) = -0,5 cos(wtri t)

sin( wtri t-2p/3 )(sin (2p/3)-sin( wtri t+2p/3 )(sin (2p/3) = - 1,5cos( wtri t )

By(t) = 1,5m0n I0 cos( wtri t )=B0 cos( wtri t ).

Montrons que le stator du moteur asynchrone crée en O un champ magnétique de valeur constante B0 tournant autour de l'axe (Oz) à la vitesse angulaire constante WB = wtri uz.

B2 = B2x(t) + B2y(t) = B20(sin2( wtri t ) +cos2( wtri t ) =B20.

La valeur du champ magnétique est constante en O : B=B0.

B= -B0 sin( wtri t )ux +B0 cos( wtri t )uy.

dB/dt = -B0wtri [cos( wtri t )ux+ sin( wtri t )uy] = WB ^ B avec WB = wtri uz.

 
 

retour -menu