mécanique des fluides : étude d'un barrage poids BTS travaux publics 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

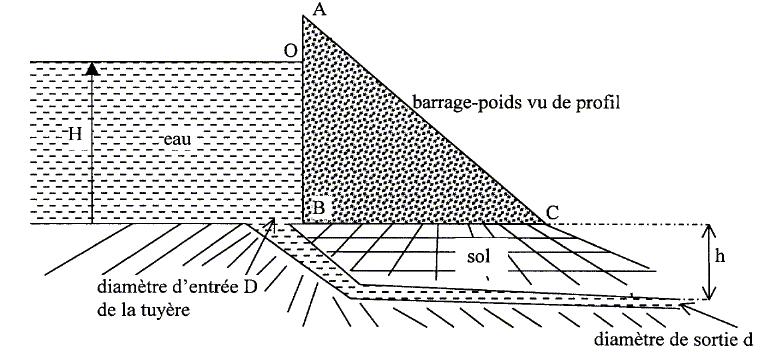
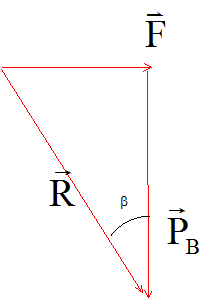
Un barrage poids a un profil assimilé à un triangle rectangle noté ABC. Il résiste à la poussée de l'eau tant que la droite d'action de la résultante des forces R s'exerçant sur la paroi coupe la base BC.

R= F+P_B, formule dans laquelle F représente la résultante des forces pressantes exercées sur la paroi AB du barrage et P_B le vecteur poids du barrage.

Le barrage poids a une hauteur AB=75 m. Le niveau de l'eau atteint une hauteur H=70 m. La largeur de sa base est BC= 56 m et sa longueur L = 1000 m.

Données : densité du béton d_B= 2,2 ; masse volumique de l'eau r_eau = 1,0 10³ kg m^-3 ; g= 9,8 N kg^-1.

Pour éviter des éventuels glissement de terrains sous l'action de la contrainte R, le barrage est équipé de 5 tuyères de sécurité. L'entrée de chaque tuyère est circulaire de diamètre D et la sortie circulaire de diamètre d. Le centre de la sortie est situé à une profondeur h= 50 m sous le niveau BC du barrage.

D= 200 cm ; d= 40 cm

Calculer le volume V_B et la masse m_B de béton utilisé lors de la construction ?

V_B = aire du triangle ABC * longueur du barrage = ½AB*BC*L

V_B =0,5*75*56*1000 =2,1 10⁶ m³.

1 m³ de béton a une masse de 2,2 tonnes

m_B= 2,2*2,1 10⁶ = 4,6 10⁶ t. ( 4,62 10⁶)

Résultante des forces pressantes F sur la paroi AB, tuyères fermées :

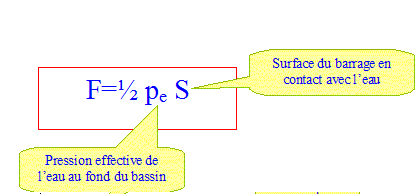
Etablir l'expression de F en fonction de r_eau, L, g et H :

S = L H ; p_e = r_eau g H

F= ½r_eau g LH².

Valeur de F :

F= 500*9,8*1000*70² = 2,4 10¹⁰ N.

Valeur de la résultante des contraintes R :

m_B= 2,2*2,1 10⁶ = 4,6 10⁶ t. ( 4,62 10⁹ kg)

P_B= 4,62 10⁹ *9,8 = 4,5 10¹⁰ N

R² = F²+P_B²=(2,4² + 4,5²) 10²⁰ = 26 10²⁰. R= 5,1 10¹⁰ N.

Calcul de l'angle b , comparer avec l'angle a au sommet du barrage :

tan b = F/P_B = 2,4 / 4,5 = 0,533 ; b = 28°.

tan a = BC/AB = 56 / 75 = 0,747 ; a = 37°.

b est inférieur à a : le barrage ne cède pas.

Comment évolue b lorsque la hauteur d'eau H augmente ?

tan b = F/P_B avec P_B constant et F proportionnelle au carré de H.

tan b étant croissante, l'angle b va croître et s'il dépasse la valeur de a, le barrage cède.

Exprimer la vitesse d'écoulement c₂ à la sortie d'une tuyère en fonction de g, H et h :

On suppose la vitesse d'abaissement c du niveau de l'eau à la surface libre du barrage négligeable devant c₂.

relation de Bernoulli : ½(c₁²-c₂²)+ g(z₁-z₂)+( P₁-P₂)/r = 0

On considère un point (1) de la surface libre de l'eau et un autre point (2) du jet d'eau à la sortie de la tuyère.

P₁=P₂ = pression atmosphérique.

de plus c₁ = c =0 d'où : -½c₂² + g(z₁-z₂) =0

c₂² = 2 g(z₁-z₂) = 2 g(H+h) ; c₂ = [2g(H+h)]^½.

Calcul de c₂ :

c₂ = (2*9,8*120)^½ = 48,5 m/s.

Calculer la vitesse d'écoulement c₁ à l'entrée de la tuyère :

conservation du débit volumique entre l'entrée et la sortie de la tuyère :

q_v = s₁ c₁ = s₂ c₂ avec s₁ = 0,25 p D² ; s₂ = 0,25 p d² ;

c₁ = c₂ d² / D² = 48,5 *(40/200)² = 1,9 m/s.

Calculer le débit volumique q_v :

q_v = s₂ c₂ = 0,25 p d²c₂ =0,25*3,14 * 0,4²*48,5 = 6,1 m³/s.

Le volume d'eau maximal du barrage est V_max = 10,0 10⁶ m³.

débit des 5 tuyères : 5*6,1 = 30,5 m³/s.

durée = V_max / débit total = 10,0 10⁶ / 30,5 = 3,3 10⁵ s = 91 h.

Rappel : relation de Bernoulli :½(c₁²-c₂²)+ g(z₁-z₂)+( P₁-P₂)/r = 0