Théorème de l'énergie cinétique ( mécanique )

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

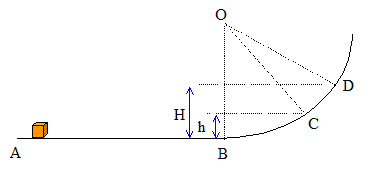
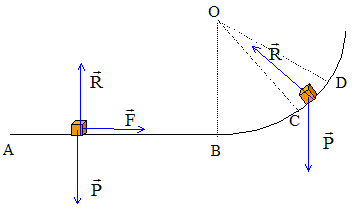
or la vitesse est da dérivée de l'abscisse par rapport au temps : v = dx/dt d'où : d(½mv²) = m dx/dt dv = m dv/dt dx

or m dv/dt =ma = F ( seconde loi de Newton) d'où d(½mv²) = F dx.  

I- Un solide (S) de masse m = 5 kg est mobile sur des rails ABC situés dans un plan vertical. AB= 4,0 m ; BD est un arc de cercle de rayon R = 10 m. (S) est initialement immobile en A. On exerce entre A et B, sur (S), une force F parallèle à AB et de valeur constante constante . Le solide monte jusqu’en D puis revient en arrière. H= 3 m ; g = 9,8 m s^–2. Les frottements sont néglileables.

théorème de l’énergie cinétique : vitesse en B

de B en D : R, perpendiculaire à la vitesse ne travaille pas. Le travail du poids est résistant ( montée) et vaut : W_P= - mgH

L'énergie cinétique en D est nulle ( arrêt) ; l'énergie cinétique en B vaut : ½mv² ( v : vitesse en B)

La variation de l'énergie cinétique est égale à la somme des travaux des forces appliquées au solide : 0-½mv² = -mgH

v²= 2gH = 2*9,8 * 3 = 58,8 ; v = 7,7 m/s.

théorème de l’énergie cinétique : valeur de F

de A en B : les forces R et P perpendiculaires à la vitesse, ne travaillent pas. Le travail de la force F vaut W_F=F AB.

L'énergie cinétique en A est nulle ( arrêt) ; l'énergie cinétique en B vaut : ½mv² ( v : vitesse en B)

La variation de l'énergie cinétique est égale à la somme des travaux des forces appliquées au solide : ½mv² -0= F AB

F= mv²/(2AB) = 5*7,7² / 8 = 36,7 N.

théorème de l’énergie cinétique : vitesse en C . ( h = 1,5 m).

de B en C : R, perpendiculaire à la vitesse ne travaille pas. Le travail du poids est résistant ( montée) et vaut : W_P= - mgh

L'énergie cinétique en C vaut ½mv²_C ; l'énergie cinétique en B vaut : ½mv² ( v : vitesse en B)

La variation de l'énergie cinétique est égale à la somme des travaux des forces appliquées au solide : ½mv²_C -½mv² = -mgh

v²_C = v² -2gh = 58,8 -2*9,8*1,5 =29,4 ; v_C = 5,4 m/s.

L'expression de cette vitesse indique que v_C ne dépend que de la vitesse en B et de l'altitude h, peut importe le sens du parcours.

ou bien appliquer le théorème de l’énergie cinétique entre les deux passages du solide en M situé sur l'arc BD à l'aller puis au retour :

R ne travaille pas ; le travail du poids est nul ( au même point la différence d'altitude est nulle). Donc l'énergie cinétique, par suite la valeur de la vitesse ne change pas à l’aller et au retour.

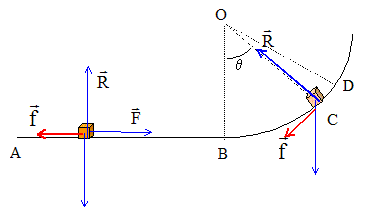
Exprimer puis calculer f et F : théorème de l’énergie cinétique :

de D en B : R, perpendiculaire à la vitesse ne travaille pas. Le travail du poids est moteur ( descente) et vaut : W_P= mgH

Le travail de f ( résistant) vaut : W_f= -f *longueur de l'arc de cercle DB = -f OC q (q en radian )

cos q = (OB-H) / OB = (10 -3) / 10 = 0,7 ; q = 0,795 rad.

L'énergie cinétique en D est nulle ( arrêt) ; l'énergie cinétique en B est nulle ( arrêt)

La variation de l'énergie cinétique est égale à la somme des travaux des forces appliquées au solide :

0-0= mgH - f *OC q d'où f = mgH /(OC q ) = 5*9,8*3/(10*0,795)= 18,5 N.

sur le trajet complet : R, perpendiculaire à la vitesse ne travaille pas. Le poids ne travaille pas ( altitude identique au départ A et à l'arrivée B)

Le travail de f ( résistant) vaut : W_f= -f (AB+2OC q ) ; le travail de F vaut W_F=F AB

L'énergie cinétique en A est nulle ( arrêt) ; l'énergie cinétique en B est nulle ( arrêt)

0-0 = -f (AB+2OC q ) + F AB soit F= f (AB+2OC q ) /AB = 18,5(4+20*0,795) / 4 = 92 N.

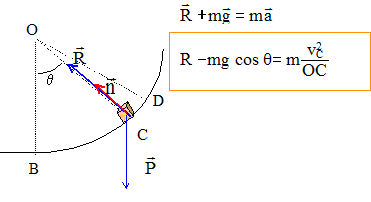
Ecrire la seconde loi de Newton sur un axe normal à la trajectoire et dirigé vers O :

R est centripète, dirigée vers O et sa valeur est : R= m[v²_C/OC + g cosq]

cos q = (OB-h) / OB = (10 -1,5) / 10 = 0,85 ; q = 31,8°.

R= 5(29,4/10+9,8 * 0,85)= 56,3 N.

Au point D le solide ne peut pas être en équilibre : la somme vectorielle des forces n'est pas nulle. durée des parcours AB et BA :

AB : écrire la seconde loi de Newton : F=ma soit a = F/m = constante ; vitesse initiale nulle :

AB=½at² = ½F/mt² soit t² = 2AB m/F = 8*5/36,7 =117,4 ; t = 1,1 s.

BA : solide pseudo-isolé , donc mouvement rectiligne uniforme . AB = vt soit t = AB/v = 4/7,7=0,52 s.

appliquer le théorème de l’énergie cinétique entre les deux passages du solide en M situé sur l'arc BD à l'aller puis au retour :

R ne travaille pas ; le travail du poids est nul ( au même point la différence d'altitude est nulle). Le travail des frottements est négatif, donc la vitesse diminue : la vitesse au retour est plus petite qu’à l’aller.

- la durée des trajets BC et CB :

La vitesse est plus faible au retour, donc la durée du retour est plus grande que celle de l’aller.

Le solide s'arrête au retour sur l'arc de cercle lorsque la somme vectorielle des forces est nulle.

L'angle q₁ vaut alors : cos q₁ = (OB-h') / OB = (10-0,5) / 10 = 0,95 ; q₁ = 0,318 rad.

A la descente le travail du poids est moteur. La force motrice est mg sin q₁ = 5*9,8*0,312 = 15,3 N, valeur insuffisante pour vaincre les frottements ( 18,5 N).

Pa r contre la force motrice en D vaut : mg sin q = 5*9,8 *0,714 =35 N valeur suffisante pour vaincre les frottements : le mobile ne reste pas en D.