Aurélie 05/10/06

 

CAPES physique chimie ( d'après concours 2006 ) Ondes électromagnétiques ; miroirs sphériques.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Les vecteurs sont écrits en gras et en bleu.
  1. Une onde électromagnétique plane progressive monochromatique et polarisée rectilignement se propage dans le vide suivant la direction de l'axe Ox.
    - Sur un schéma représenté un plan d'onde, les vecteurs champ électrique E, champ magnétique B ainsi que le vecteur d'onde k. 
    - Ecrire la relation liant ces trois vecteurs.
    - Que signifie "onde polarisée rectilignement " ?
    - Il existe des situations où la lumière naturelle est polarisée. Citer deux exemples.
  2. On désire réaliser l'image d'une région du ciel nocturne sur un capteur CCD de 2,54 cm de côté. Les cellules de la matrice CCD sont des carrés juxtaposés de 10,0 mm de côté. Deux étoiles sont séparées si leurs images se forment sur deux cellules CCd non consécutives ( c'est à dire deux cellules sépérées par une cellule faiblement éclairée). Les applications numériques seront faites en supposant que les images des étoiles considérées se forment au centre d'une cellule du capteur.
    - On imagine d'abord utiliser une lentille de distance focale 1,5 m. Comment faut-il disposer le capteur par rapport à la lentille pour que la qualité de l'image soit optimale ? Justifier.
    - Expliquer pourquoi l'onde parvenant de l'étoile sur la lentille peut être considérée comme une onde plane.
    - Quel angle a doit séparer les directions de visées de deux étoiles pour qu'elles soient juste séparées ? Comparer cet angle au pouvoir séparateur de l'oeil ( 3 10-4 rad).
  3. Le schéma ci-dessous représente un miroir sphérique M de centre C et de rayon de courbure R. L'objet AB est placé à gauche de C, perpendiculairement à l'axe du miroir.

    - Pour un miroir la relation de conjugaison avec origine au centre s'écrit : 1/CA + 1/CA' = 2 / CS ( en gras les distances algébriques)
    S désigne le sommet du miroir. Utiliser cette formule pour trouver la position du foyer du miroir.
    - Construire l'image A'B' que donne le miroir de l'objet AB.
    - Pour obtenir l'image d'une région du ciel, on souhaite utiliser à la place de la lentille, un ensemble de deux miroirs sphériques M1 et M2 de même centre C, de rayon respectifs R1 = 1,20 m et R2. Le miroir M1 présente une ouverture circulaire auour de son sommet S1. Cet ensemble de miroirs se comporte comme une lentille dont nous allons déterminer les caractéristiques.

    - En imaginant de placer une source lumineuse ponctuelle entre les miroirs construire le trajet d'un rayon issu de la source et dirigé vers le point C. En déduire la position du centre de la lentille équivalente à l'ensemble des deux miroirs.
    - En utilisant deux fois la relation de conjugaison, trouver la relation liant les positions d'un objet AB et de son image A'B' donnée par l'ensemble des deux miroirs. En déduire l'expression de la distance focale de la lentille équivalente en fonction de R1 et R2.
    - En prenant R1=1,20 m, calculer R2 pour que l'ensemble des deux miroirs ait la même distance focale que la lentille utilisée dans la question 2. Préciser sur un schéma comment il faudra placer le capteur CCD pour observer l'image du ciel.
    - Citer deux avantages du système de deux miroirs par rapport à la lentille.

 


 corrigé

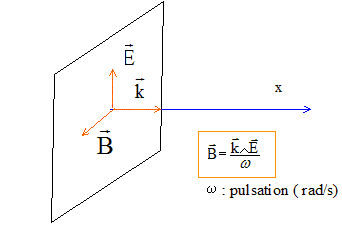
"onde polarisée rectilignement " :

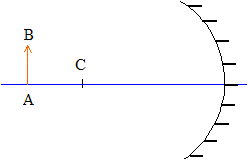
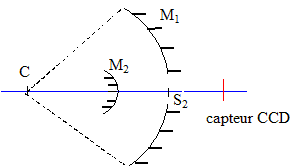
les vecteurs champ magnétique et champ électrique ont toujours la même direction.
Situations où la lumière naturelle est polarisée :

après réflexion sur une surface métallique polie, après diffusion par le ciel perpendiculairement au rayon incident, la lumière est en partie polarisée.

On désire réaliser l'image d'une région du ciel nocturne sur un capteur CCD de 2,54 cm de côté. Les cellules de la matrice CCD sont des carrés juxtaposés de 10,0 mm de côté. Deux étoiles sont séparées si leurs images se forment sur deux cellules CCd non consécutives ( c'est à dire deux cellules sépérées par une cellule faiblement éclairée). L'objet (étoile) étant située à l'infini, et pour travailler dans les conditions de Gauss ( images de bonne qualité), il faut disposer le centre du capteur au foyer principal image de la lentille.

De plus le plan contenant le capteur doit être perpendiculaire à l'axe optique principal de la lentille.
L''onde parvenant de l'étoile sur la lentille peut être considérée comme une onde plane : onde sphérique dont le rayon est très supérieur aux dimensions de la lentille.
Angle a séparant les directions de visées de deux étoiles pour qu'elles soient juste séparées :

tan a = disatance du centre du carré n°1 au centre du carré n°3 divisée par la distance focale de la lentille.

l'angle étant petit, on peut confondre la tangente avec sa mesure en radian :

a = 2*10-5 / 1,5 = 1,3 10-5 rad.

cet angle est environ 20 fois inférieur au pouvoir séparateur de l'oeil ( 3 10-4 rad).

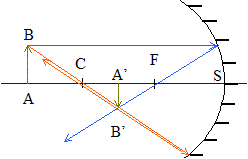
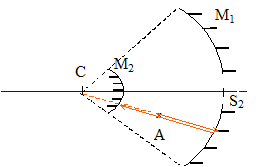
Pour un miroir la relation de conjugaison avec origine au centre s'écrit : 1/CA + 1/CA' = 2 / CS ( en gras les distances algébriques)
S désigne le sommet du miroir.

la position du foyer F du miroir :

l'image d'un étoile située à l'infini se forme au foyer F ; 1/CA =0 d'où CA'= CF = ½ CS.
Construction de l'image A'B' que donne le miroir de l'objet AB :

Pour obtenir l'image d'une région du ciel, on souhaite utiliser à la place de la lentille, un ensemble de deux miroirs sphériques M1 et M2 de même centre C, de rayon respectifs R1 = 1,20 m et R2. Le miroir M1 présente une ouverture circulaire auour de son sommet S1. Cet ensemble de miroirs se comporte comme une lentille dont nous allons déterminer les caractéristiques.

position du centre de la lentille équivalente à l'ensemble des deux miroirs :

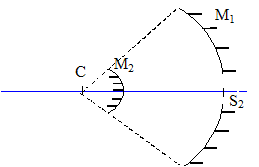
Tout rayon issu de A et passant par le foyer, n'est pas dévié après réflexion sur les miroirs : le point cherché est le point C.

Relation liant les positions d'un objet AB et de son image A'B' donnée par l'ensemble des deux miroirs :

image A1B1 donnée par le miroir M1 d'un objet AB : 1/CA + 1/CA1 = 2 / CS1= 2 /R1.(1)

A1B1 joue le rôle d'objet pour le miroir M2 ; l'image définitive est notée A2B2 :

1/CA1 + 1/CA2 = 2 /R2.(2)

(2)-(1) donnent : 1/CA2 -1/CA = 2 /R2 -2 /R1.

Expression de la distance focale de la lentille équivalente en fonction de R1 et R2 : 1/CF' = 2 /R2 -2 /R1.
En prenant R1=1,20 m, calcul de R2 pour que l'ensemble des deux miroirs ait la même distance focale que la lentille utilisée dans la question 2 :

2 /R2 = 1/CF' + 2 /R1 = 1/1,5 + 2/1,2 = 2,33 ; R2 = 2/2,33 = 0,86 m.

pour observer l'image du ciel il faut placer le capteur CCD au foyer F' tel que : CF' =1,5 m.


Avantages du système de deux miroirs par rapport à la lentille : ensemble plus réduit et absence d'aberrations chromatiques.



retour -menu