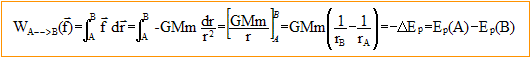|
CAPES physique chimie ( concours interne 2005) Mouvement d'un satellite dans le champ de gravitation terrestre En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||
| .
. |
||||
|
||||
|
|
Un satellite S, assimilable à un point matériel de masse m, est soumis uniquement à la force gravitationnelle de la Terre. La Terre est considérée come un corps sphérique homogène de rayon R, de masse M et de centre O. La Terre tourne sur elle même, autour de sa ligne des pôles, à la vitesse angulaire W. On ne considère pas son mouvement de révolution autour du soleil. On travaille dans le référentiel géocentrique et dans le repère cylindrique, où le plan polaire est confondu avec la trajectoire du satellite. On désigne par r(t)= OS, le vecteur position du satellite et par v(t) = dr/dt, sa vitesse. 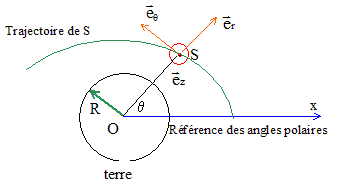
On considère que le satellite décrit une orbite circulaire à l'altitude h.
corrigé référentiel : objet par rapport auquel on se repère pour l'étude du mouvement d'un système ; on lui associe un repère et une origine des temps. référentiel galiléen : dans ce référentiel le principe d'inertie ou 1ère loi de Newton s'applique " un point matériel pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne uniforme". Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes. Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique. Ce référentiel peut être considéré comme galiléen pour des durées de quelques minutes. ( La Terre effectue un mouvement de rotation autour d'un axe nord sud) Expression vectorielle du champ de force f(r) auquel est soumis le satellite : Le satellite n'est soumis qu'à la force de gravitation attractive exercée par la Terre. La direction de cette force passe toujours par le point O, centre de la Terre : il s'agit donc d'un champ de forces centrales. f(r) = GMm/r2(-er) Montrons que la force f qui s'exerce sur le satellite S dérive d'une énergie potentielle de gravitation Ep. Le travail de la force f(r) ne dépend que des positions initiale et finale ( peu importe le chemin suivi) : la force est conservative. On peut associer à cette force, une fonction scalaire ou énergie potentielle notée Ep(r), définie à une constante près ; la variation de l'énergie potentielle entre les points A et B est égale à l'opposée du travail de la forcef(r) entre ces points.
En prenant B situé à l'infini ( par convention cette énergie potentielle est nulle à l'infini), il vient : Ep = -GMm/r. Pour éloigner deux masses l'une de l'autre, il faut exercer un travail moteur, opposé au travail de la force de gravitation donc égal à la variation d'énergie potentielle : DEp >0 ; Ep fin - Ep initial >0 ; or Ep fin tend vers zéro donc Ep initial <0 l'énergie potentielle de gravitation est donc négative quelle que soit la distance r finie Le signe négatif dans le terme d'énergie potentielle
traduit le fait que celle-ci augmente si R croît.
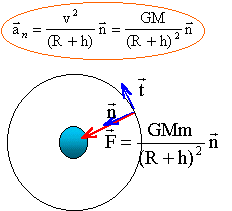
On considère que le satellite décrit une orbite circulaire à l'altitude h. Montrons que la trajectoire circulaire implique un mouvement uniforme : Le satellite n'est soumis qu'à la force de gravitation centripète ; cette force est à chaque instant perpendiculaire à la vitesse et en conséquence sa puissance est nulle. L'énergie cinétique du satellite ne varie pas : donc la valeur de la vitesse est constante ( mouvement uniforme). Expression de la vitesse v et la période T de ce satellite en fonction de G, M, R, h : le satellite est soumis à la seule force de gravitation centripète exercée par la planète
M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m aN= mv²/ (R+h) d'où la valeur de la vitesse (m/s): v² =GM / (R+h). indépendante de la masse du satellite La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p (R+h) =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² (R+h) ² = v² T² = GM/ (R+h) T² ou T² =4p² /(GM)(R+h)3. soit T² /(R+h)3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) distance en mètre, période en seconde, masse en kg. Déterminons l'altitude qu'il faut atteindre pour obtenir la période de rotation de 101 min de spot 1: T= 101 min = 101*60 = 6060 s ; G= 6,67 10-11 SI ; M= 5,98 1024 kg ; (R+h)3 = T2GM/(4p2)=60602 * 6,67 10-11 * 5,98 1024 / (4*3,142)=3,72 1020 . R+h = 7,19 106 m ; h = 7,19 106- 6,37 106 = 8,18 105 m = 818 km. Calcul de la vitesse du satellite : v=[GM/(R+h)]½ =[6,67 10-11 * 5,98 1024 / 7,19 106 ]½ = 7,45 103 m/s, inférieure à la vitesse de libération terrestre. La vitesse de libération d'un corps quittant la Terre
est de l'ordre de 11,2 103 m/s.
Ec = ½mv2 ; Ep= -GMm/r avec v2= GM/r soit Ep= - mv2 ; Em = Ec+ Ep= -½mv2 ; Une relation simple existe entre Em
et Ec : Em
= - Ec.
La vitesse linéaire transmise par la Terre à un corps lancé depuis sa surface est : à l'équateur : v = W R = 7,3 10-5 * 6,37 106 = 463 m/s. à la latitude l = 28°N : vl= W R cos l = 7,3 10-5 * 6,37 106 cos 28 = 409 m/s. Cette vitesse, tangente à la surface du globe est dirigée vers l'Est. Une base de lancement proche de l'équateur conduit à une vitesse initiale de lancement plus grande que celle d'un site situé à une latitude supérieure. Cela est un énorme avantage : cette vitesse additionnée vectoriellement avec la vitesse de la fusée porteuse, détermine la vitesse finale du satellite.
Le satellite S est lancé à partir d'une base terrestre proche de l'équateur de la Terre. Expression de l'énergie mécanique Esol de ce satellite dans le référentiel géocentrique avant son lancement : l'énergie potentielle vaut Ep= -GMm/R ; l'énergie cinétique communiquée par la Terre vaut : Ec = ½mv2 avec v = 463 m/s l'énergie mécanique vaut : Esol = -GMm/R + ½mv2 Esol =-6,67 10-11*5,98 1024*1830/6,37 106 + 915*4632 = -1,1439 1011 J Le satellite est lancé depuis Cap Canaveral( l= 28°N). l'énergie mécanique vaut : Esol = -GMm/R + ½mvl2 Esol =-6,67 10-11*5,98 1024*1830/6,37 106 + 915*4092 = -1,1443 1011 J Energie mécanique finale du satellite à l'altitude h=818 km : Em=-Ec=-½m*(7,45 103 )2= - 915*(7,45 103 )2= -5,078 1010 J Energie minimale W0 dépensée pour placer le satellite sur orbite : Energie mécanique finale - Energie au sol = -5,078 1010
+1,1439 1011 = 6,360 1010
J Energie mécanique finale - Energie au sol = -5,078 1010
+1,1443 1011 = 6,365 1010
J |
|||
|
|
||||
|
|