CAPES physique chimie ( concours interne 2005 ) Etude cinétique de la synthèse du diiode suivie par spectrophotométrie.

Aurélie 03/10/06

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

On se propose de déterminer l'ordre et la constante de la réaction d'oxydation des ions iodures par le peroxodisulfate S₂O₈^2- en solution aqueuse. Seule le ddiode est coloré. E°(I₂/I^- ) = 0,62 V ; E°(S₂O₈^2-/SO₄^2- ) = 2,01 V
- Ecrire l'équation de la réaction étudiée.
- Exprimer puis calculer sa constante d'équilibre. Conclure.
Des études expérimentales montrent que la vitesse de cette réaction dépend uniquement de la concentration en ions I^- et S₂O₈^2-. La vitesse de la réaction s'écrit : v = -d[S₂O₈^2-]/dt = k[I^-]^a[S₂O₈^2-]^b. Cette réaction est étudiée à température ambiante. A l'instant t=0 on mélange un volume V₁= 15,0 mL d'une solution de peroxodisulfate d'ammonium de concentration c₁ = 6,25 10^-3 mol/L et un volume V₂ = 25,0 mL de solution d'iodure de potassium de concentration C₂ = 0,250 mol/L.
- Soit c₀ la concentration initiale de S₂O₈^2-et c celle de I^- dans le mélange. Qu'observe t-on ? Simplifier alors la loi de vitesse en introduisant la constante k', constante de vitesse apparente.
- Ecrire le bilan de matière en concentration en notant x l'avancement volumique de la réaction en mol/L. A un instant de date t, exprimer [S₂O₈^2-]_t en fonction de [I₂]_t.
- A partir de la loi de vitesse obtenue, sachant que b=1, établir la loi cinétique en [S₂O₈^2-]_t. Quelle courbe faut-il tracer pour vérifier la valeur de b ?

Des mesures de l'absorbance de la solution en fonction du temps donnent les résultats suivants :

t en min 0 4 8 12 16

a 0 0,349 0,670 0,940 1,178

- Montrer que ces résultats sont en accord avec b =1.
- Calculer la constante apparente de vitesse.
- En déduire la constante de vitesse si on suppose que a=1.

corrigé

équation de la réaction entre les ions peroxodisulfate et les ions iodure :

2I^- = I₂+ 2e^-; E₁ = E°(I₂/I^- ) + 0,03 log ([I₂]/[I^-]²)

S₂O₈^2-+ 2e^-= 2SO₄^2-; E₁ = E°(S₂O₈^2-/SO₄^2- ) + 0,03 log ([S₂O₈^2-]/[SO₄^2-]²)

2I^-+S₂O₈^2- = I₂+2SO₄^2-; K=[I₂][SO₄^2-]² / ([S₂O₈^2-][I^-]²)

à l'équilibre : E₁=E₂ ; E°(I₂/I^- ) + 0,03 log ([I₂]/[I^-]²) = E°(S₂O₈^2-/SO₄^2- ) + 0,03 log ([S₂O₈^2-]/[SO₄^2-]²)

E°(S₂O₈^2-/SO₄^2- ) - E°(I₂/I^- ) = 0,03[log ([I₂]/[I^-]²) - log ([S₂O₈^2-]/[SO₄^2-]²)]

E°(S₂O₈^2-/SO₄^2- ) - E°(I₂/I^- ) = 0,03 log [I₂][SO₄^2-]² / ([S₂O₈^2-][I^-]²) = 0,03 log K

log K = (2,01-0,63) / 0,03 = 46,3 ; K = 2 10⁴⁶.

K est très grande : l'équilibre est fortement déplacé dans le sens direct, vers la droite ; la réaction est totale.

Soit c₀ la concentration initiale de S₂O₈^2-et c celle de I^- dans le mélange.

c₀ = c₁V₁ / (V₁+V₂) = 6,25 10^-3 * 15/40 = 2,34 10^-3 mol/L

c = c₂V₂ / (V₁+V₂) = 0,25*25/40 = 0,156 mol/L

c est très supérieure à c₀, on peut considérer que la concentration des ions iodures est constante ( large excès d'ions iodure)

La loi de vitesse se simplifie : v = -d[S₂O₈^2-]/dt = k[I^-]^a[S₂O₈^2-]^b = k' [S₂O₈^2-]^b avec k' = k[I^-]^a , constante de vitesse apparente.
Bilan de matière en concentration en notant x l'avancement volumique de la réaction en mol/L.

avancement volumique mol/L 2I^- +S₂O₈^2- = I₂ +2SO₄^2-

initial 0 c c₀ 0 0

en cours x c-2x c₀-x x 2x

A un instant de date t, [S₂O₈^2-]_t = c₀-x ; [I₂]_t = x d'où : [S₂O₈^2-]_t = c₀-[I₂]_t
;-d[S₂O₈^2-]/dt = d[I₂]_t / dt ; v = d[I₂]_t / dt = k' [S₂O₈^2-]

Loi cinétique en [S₂O₈^2-]_t :

-d[S₂O₈^2-]/dt =k' [S₂O₈^2-] ; d ln[S₂O₈^2-] = -k'dt

intégrer entre 0 et t : ln[S₂O₈^2-]- ln c₀ = -k't ; ln ( [S₂O₈^2-]/ c₀) = -k't ou [S₂O₈^2-] = c₀ exp(-k't)

Pour vérifier la valeur b = 1, il faut tracer la courbe d'équation ln ( [S₂O₈^2-]/ c₀) = f(t), droite passant par l'origine de coefficient directeur k'.

Des mesures de l'absorbance de la solution en fonction du temps donnent les résultats suivants :

t en min	0	4	8	12	16
A	0	0,349	0,670	0,940	1,178

L'absorbance A est proportionnelle à [I₂]_t: [I₂]_t = K A avec K= constante

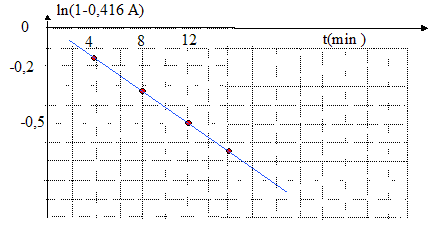
or [I₂]_t = c₀-[S₂O₈^2-]_t = c₀-c₀ exp(-k't) ; [I₂]_t = c₀(1-exp(-k't)) ; A_t = c₀/ K(1-exp(-k't))

A_tK/c₀=1-exp(-k't) ; 1-A_tK/c₀=exp(-k't) ; ln(1-A_tK/c₀) = -k't

Détermination de K/c₀ :

ln(1-A₄K/c₀) = -4k' ; ln(1-A₈K/c₀) = -8k' ; ln(1-A₄K/c₀) - ln(1-A₈K/c₀) = 4k' ;

ln((1-A₄K/c₀) / (1-A₈K/c₀) ) = 4k'

de même : ln((1-A₈K/c₀) / (1-A₁₂K/c₀) ) = 4k'

d'où (1-A₄K/c₀) / (1-A₈K/c₀) = (1-A₈K/c₀) / (1-A₁₂K/c₀)

(1-0,349K/c₀) / (1-0,67K/c₀) = (1-0,67K/c₀) / (1-0,94K/c₀)

La constante K/c₀ vaut 0,416.

en conséquence : ln(1-0,416A_t) = -k't

On trace la courbe ln(1-0,416A_t) = f(t) :

La courbe est une droite ce qui confirme la valeur b =1.
Constante apparente de vitesse : valeur absolue du coefficient directeur de la droite : k' = 4,1 10^-2 mn^-1
Constante de vitesse si on suppose que a=1 : k' = k[I^-] ; k = k' / [I^-] = 4,1 10^-2 / 0,156 = 0,26 min^-1L mol^-1.

retour -menu