|
CAPES physique chimie ( d'après concours interne 2003 ) La clepsydre : mécanique des fluides En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
La clepsydre est une horloge à eau constituée d'un vase percé d'un trou . Le vase a une forme évasée, plus large vers le haut ( le débit est plus grand quand la hauteur d'eau est plus grande). Dans ce cas, des graduations presque équidistantes permettent de mesurer des intervalles de temps. On se place dans un référentiel galiléen (R) d'origine O. Soit une particule fluide de volume dV, de masse dm, qui se trouve en un point M à une date t. Les grandeurs relatives à cette particule sont notées : v pour la vitesse, r pour la masse volumique, p pour la pression, z pour l'altitude. Fluide parfait :
Relation de Bernoulli : p/r + gz + ½v² = constante. g représente la valeur du champ de pesanteur terrestre.
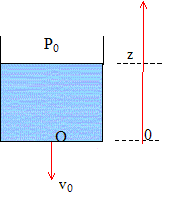
Une approche de la clepsydre : Un récipient cylindrique de hauteur H est rempli d'eau jusqu'à une hauteur h. Le sommet du récipient de section S est ouvert à l'air libre où il règne la pression atmosphérique P0. A l'instant t=0 on ouvre un orifice O de section faible s, au fond du réservoir. On admet que les veines liquides ont à la sortie du trou la même section que l'orifice. On note vL la vitesse de descente de la surface libre de l'eau et v0 la vitesse de sortie de l'eau en O. On considère que la section S est très supérieure à la section s. H= 50 cm ; h = 40 cm ; P0 = 1 bar ; s = 1 cm² ; g= 10 N/kg. Le récipient cylindrique a un rayon R= 30 cm.
Au point de vue énergétique, ce fluide parfait ne dissipe pas d'énergie cinétique. définition macroscopique de la pression exercée par un fluide parfait : La pression, notée p( Pa), est le quotient d'une force F ( N) sur l'aire de la surface S(m²) sur laquelle elle s'applique. unités de pression couramment utilisées : 1 bar = 105 Pa 1 atm = 101 325 Pa (atm = Atmosphère) 1 mm Hg = 1 torr = grh9,8*13600*10-3 = 133 Pa (mmHg = millimètre de mercure) 1 psi = 6 894 N/m2 = 6 894 Pa = 0,068 94 bar (psi = livre par pouce carré, unité anglo-saxonne) écoulement fluide en régime permanent ou stationnaire : Les composantes de la vitesse sont indépendantes du temps. ligne de courant : courbe dont la tangente en chacun de ses points est la direction du vecteur vitesse. tube de courant : ensemble de lignes de courant s’appuyant sur un contour fermé. conservation locale de la masse pour un fluide parfait imncompressible en écoulement permanent unidirectionnel. Soit un élément de volume dV autour d'un point M ; sa masse est notée dm = d(rV) = constante ou encore div( r V)=0 avec V: vecteur vitesse ; r : masse volumique div( r V)=0
traduit le fait qu'il n'y a pas d'accroissement de matière autour du
point M.
Cette relation peut être applicable à tout le fluide si : le fluide est incompressible (r constant), "parfait" ( viscosité nulle), en régime permanent et sans transfert de chaleur. interprétation énergétique de cette relation : Cette relation traduit la conservation de l'énergie le long d'une ligne de courant. ½rv² : énergie cinétique par unité de volume ou densité d'énergie cinétique r gz : densité d'énergie potentielle de gravitation p : densité d'énergie élastique. analyse dimensionnelle : [½v²] = L2T-2 ; vitesse ² = distance ²/ temps² gz : accélération * distance ; accélération = distance / temps2 d'où : [gz] = L2T-2 ; p/r : pression = force / surface ; force = masse * accélération = masse * distance / temps² masse volumique = masse / volume = masse / distance3 d'où [p/r]= L2T-2 ; Les trois termes ont la même dimension, donc
l'expression de Bernoulli est homogène.
Expression la vitesse v0 en fonction de g et z, cote de la surface libre à l'instant t : S>>s la vitesse d'un point de la surface libre est négligeable devant v0. On considère un point situé à la surface du liquide et un point situé au contact de l'air à la sortie du trou O : en ces deux points la pression est identique et vaut P0. En ces deux points le théorème de Bernoulli s'écrit : gz = ½v²0 soit v0 = [2gz]½. Equation différentielle à laquelle obéit z : écrire la conservation du débit volumique en A, point de la surface et en O : S vL= s vO avec vL= -dz/dt -Sdz/dt = s vO = s [2gz]½ ; dz/dt +s/S[2gz]½ =0. Expression traduisant les variations de z en fonction du temps : séparer les variables : dz / z½ = -s/S [2g]½ dt intégrer entre 0 et t : 2[z½]z0z = -s/S [2g]½ [t]0t ; 2[z½-z0½]= -s/S [2g]½ t soit 2[z0½-z½]= s/S [2g]½t. Temps au bout duquel le cylindre sera complètement vide : z=0 2z0½= s/S [2g]½t ; t = S/s[2z0/ g]½ avec S= pR²= 3,14*0,3²= 0,283 m² ; s = 10-4 m² ; z0= 0,4 m t = 0,283/10-4 0,08½= 800 s. On souhaite réaliser à l'aide de ce dispositif une horloge qui permette de mesurer des durées t= 1 min. La cote de la surface de l'eau à la date t=0 est notée z0. Calcul de z1, cote de la surface de l'eau à la date t= t : 2[z0½-z½]= s/S [2g]½t = 10-4 / 0,283 *20½*60 = 0,0948 ; z0½-z½ = 0,0474 ; z½ =z0½- 0,0474 = 0,4½-0,0474 =0,585 ; z1 = 0,342 m = 34,2 cm. Calcul de z2, cote de la surface de l'eau à la date t=2 t : 2[z0½-z½]= s/S [2g]½t = 10-4 / 0,283 *20½*120 = 0,1896 ; z0½-z½ = 0,0948 ; z½ =z0½- 0,0948 = 0,4½-0,0948 =0,538 ; z2 = 0,289 m = 28,9 cm. inconvénient d'un tel dispositif pour la mesure du temps : les graduations ne sont pas équidistantes. |
|
|
|
||
|
|