|
CAPES physique chimie ( d'après concours interne 2002 ) Réalisation d'un générateur idéal de tension Diverses méthodes de mesure d'une résistance En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||
| .
. |
||||||||||||||||||||||
|
||||||||||||||||||||||
|
|
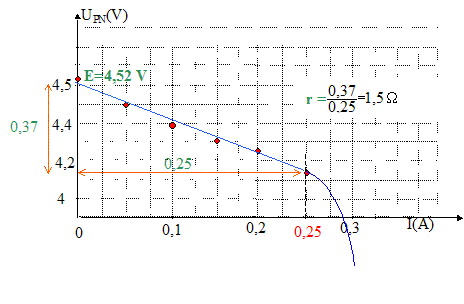
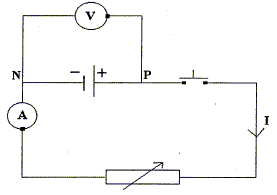
On relève les valeurs de UPN et celle de I :
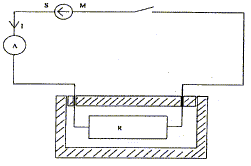
Dans le circuit ci-dessous, C est un condensateur initialement déchargé de capacité C, K est un conducteur ohmique calibré de haute précision, de résistance K= 220 W. On branche aux bornes du condensateur un oscilloscope à mémoire qui déclenche l'aquisition des mesures à la fermeture de l'interrupteur, c'est à dire à la date t=0. 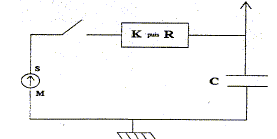
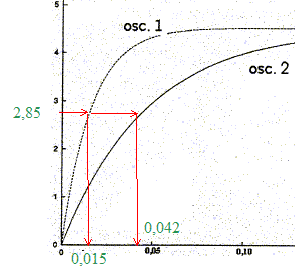
On obtient l'oscillogramme 1. On ouvre ensuite le circuit, on décharge le condensateur, on remplace le conducteur ohmique K par le conducteur ohmique R, on ferme à nouveau l'interrupteur et on obtient l'oscilloframme 2. 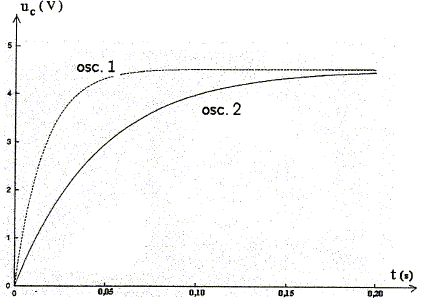
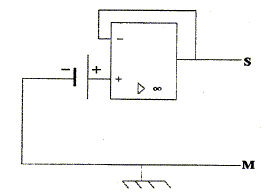
On réalise d'abord la charge du condensateur C' à l'aide du générateur idéal SM en plaçant l'interrupteur en position 1. Le condensateur étant chargé on bascule l'interrupteur en position 2. Un ordinateur permet de suivre l'évolution de la tension aux bornes du condensateur.
On dispose d'un calorimètre dont l'ensemble cuve et accessoires a une capacité thermique Cth=120 J K-1. On verse dans le calorimètre un volume d'eau tiède de valeur V= 100,0 mL, et après quelques minutes, on mesure la température qi=17,0°C. On pèse un bloc de glace ( mg= 88,7 g) pris à la température qg=-20,0°C et on le plonge dans l'eau contenue dans le calorimètre.
Données : ceau = 4180 J kg-1 K-1 ; cglace =2100 J kg-1 K-1 ; Lfusion = 335 103 J kg-1.
utilité du bouton poussoir : Il permet de fermer le circuit pendant une durée très courte, suffisamment longue pour effectuer chaque lecture de la tension et de l'intensité ; entre deux mesures la pile de débite pas ; ainsi la pile ne se déchargera pas trop durant la durée de toutes les mesures. Lorsque l'intensité délivrée par le générateur est inférieure àI=0,25 A, la pile peut être considérée comme un dipôle linéaire.
E=4,52 V et r = 1,5 W ; équation de sa caractéristique : UPN=E-rI = 4,52 - 1,5 I. Le montage avec l'A.O idéal est un montage suiveur : la tension d'entrée est égale à la tension de sortie UPN=USM ; or l'intensité des courants dans les entrées E+
et E- de l'A.O sont pratiquement nulles (
impédance d'entrée très grande) : en conséquence UPN=E=4,52
V =USM
additivité des tensions : uc + Ri = E or i = dq/dt = q' et q=Cucd'où i= C u'c par suite : uc + Ri = E s'écrit : uc + RC u'c = E ; on pose t = RC, constante de temps du dipôle RC. uc + t u'c = E. (1) Expression littérale de la fonction uc(t) ; t=0 correspond à la date de fermeture de l'interrupteur : solution particulière de (1) : uc=E ( condensateur chargé) solution générale de uc + t u'c = 0 : uc(t) = A exp(-t/t). solution générale de (1) : uc(t) = A exp(-t/t) + E On détermine la constante A à partir de la condition initiale : à t=0, le condensateur n'est pas chargé, soit uc(t) =0. uc(0) =0= A exp(0) + E = A+E soit A=-E uc(t) = E(1- exp(-t/t) ). Lecture de la valeur de t sur le graphique : à t=t, uc(t) = E(1- exp(-1) ) = 0,63 E = 0,63*4,52 = 2,85 V
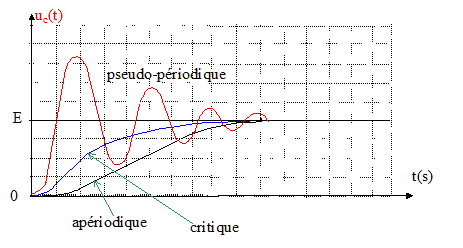
Transferts d'énergie mis en jeu dans le circuit : ( régime apériodique) échange permanent d'énergie entre bobine et condensateur ; au cours de ces échanges, une partie de l'énergie est dissipée par effet joule dans les conducteurs ohmiques. Si la valeur de K est forte, on se trouve en régime apériodique. Il existe une valeur de la résistance K pour laquelle l'évolution de la tension aux bornes du condensateur est dite "critique", à la frontière des deux régimes évoqués précédemment. L'utilisation de l'outil informatique permet de mémoriser les courbes obtenues en faisant varier lentement K et de repèrer le passage au régime critique ( voir évolution des courbes ci-dessus) Le régime critique est obtenu pour K= 189 W. L'étude théorique prévoit qu'il est obtenu lorsque la résistance totale du circuit vaut : Rtotale = 2(L/C')½. Homogénéité de cette expression : énergie stockée par une bobine inductive : E=½LI² soit L = 2E/I² L'inductance est une énergie divisée par une intensité au carré : joule ampère -2. énergie stockée par le condensateur : E=½C'U² soit C'= 2E/ U² la capacité est une énergie divisée par une tension au carré : joule volt-2. par suite L/C' a la dimension de : volt2 ampère -2 et (L/C')½ a la dimension d'une résistance soit volt ampère -1 Calcul de la valeur de R : Rtotale = 2(L/C')½ = 2(0,4 / 2,2 10-6)½ = 853 W. Rtotale =R+K+r ; R= Rtotale
-K-r = 853-186-20 = 644 W.
vase adiabatique ( pratiquement pas d'échange avec le milieu extérieur) paroi interne brillante (en verre) limitant le rayonnement vide entre les doubles parois : pas de convection parois externe isolante : pas de conduction A l'équilibre thermique la température à l'intérieur du calorimètre vaut qéq=0,0°C : hypothèse : toute la glace glace fond à 0°C et la température finale est 0°C. énergie gagnée par la glace pour se réchauffer de -20 °C à 0°C sans fondre : Q1 = mg cglace(0-qg)= mg cglaceqg=88,7 10-3*2100*20 = 3725 J énergie gagnée par la glace pour fondre à °C : Q2 = mgLfusion =88,7*335 = 29714 J Q1 + Q2 = 3725 + 29714 = 33439 J Energie cédée par les corps chauds, eau ( 100 g = 0,1 kg) et calorimètre : Q3= (0,1ceau + Cth)(0-qi) = (0,1*4180+120)*(-17) = - 9146 J Or |Q3| < Q1 + Q2 donc toute la glace ne peut fondre ; cette hypothèse est fausse. Le mélange final contient de l'eau et de la glace : sa température est 0°C. hypothèse : une masse m1g de glace fond à 0°C. 3725 J sont nécessaire pour réchauffer 88,7 g de glace de -20 à 0°C ; il reste donc : 9146-3725 = 5421 J pour faire fondre une masse m1g de glace à 0°C 5421 = m1g Lfusion ; m1g = 5421 / 335 103 = 16,2 g. dans le calorimètre à l'équilibre thermique : masse
d'eau m'= 100+16,2 = 116,2
g ; masse de glace m'g =
88,7-16,2 = 72,5 g.
hypothèses faîtes pour le bilan énergétique : vase adiabatique, capacité thermique massique du métal constituant la résistance R, négligeable. Energie nécessaire pour faire fondre une masse m'g = 72,5 g de glace à 0 C : Q4 = m'gLfusion =72,5*335 = 24287 J Energie fournie par effet joule : Q= RI²t avec I= 0,294 A et t = 421 s. Q4 =Q soit R= m'gLfusion /(I²t) = 24287/(0,2942*431) = 652 W. Cette dernière méthode est sans doute la plus précise. Pour la première, les constantes de temps sont peu précises ; pour la seconde r et K sont peu précises. Estimation numérique de l'incertitude relative sur la valeur de R : log R= log m'g + log Lfusion - 2 log I-log t d'où DR/R= Dm'g/m'g + 2DI/I + Dt/t = 0,1/75,2 + 2/294 + 1/431 voisin de 10-2 ( 1%) |
|||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
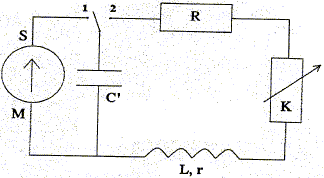 C'=
2,2 mF; L= 0,40 H ; r=
20 W.
C'=
2,2 mF; L= 0,40 H ; r=
20 W.