Aurélie 26/10/06

 

Agrégation physique chimie ( concours 2006 ) : pile de concentration

stoechiométrie et la constante globale de formation bn du complexe Ag(NH3)2+ en solution aqueuse

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


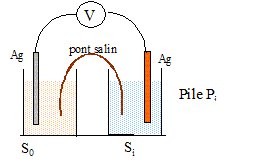
But : déterminer la stoechiométrie et la constante globale de formation bn du complexe Ag(NH3)n+ en solution aqueuse.

On considère les solutions Si ( i=0, 1, 2, 3) préparées de la manière suivante : dans une fiole jaugée de 100 mL, on place un volume v0 = 20 mL d'une solution de nitrate d'argent à c0=1,0 10-2 mol/L et un volume vi (mL) d'une solution d'ammoniac à 1 mol/L puis on complète au trait de jauge avec de l'eau distillée.
solution
S0
S1
S2
S3
v0 (mL)
20
vi (mL)
0
20
40
60

  1. Ecrire l'équation bilan de la réaction globale de formation du complexe Ag(NH3)n+ dans la solution Si.
  2. Donner en fonction de vi et n l'expression des concentrations à l'équilibre [Ag(NH3)n+] et [NH3]i. Quel est l'intérêt d'utiliser une solution d'ammoniac concentrée ?
  3. On réalise la pile suivante pour chaque solution Si :
    - Comment nomme t-on une telle pile ?
    - Rappeler l'expression de la formule de Nernst pour le couple Ag+/Ag.
    - Montrer que la mesure de la ddp DEi= Ei-E0 entre les électrodes d'argent permet de déterminer les valeur de n et bn.
    - Justifier le signe négatif de DEi.
    - Exploiter les mesures du tableau ci-dessous :
    pile
    P1
    P2
    P3
    DEi(mV)
    -342
    -374
    -392
    La constante de formation du complexe ammine argent (I) a pour valeur 103,4. Vérifier que dans les conditions de l'expérience on peut négliger la formation de ce complexe.



 

corrigé
Equation bilan de la réaction globale de formation du complexe Ag(NH3)n+ dans la solution Si :

Ag+ + n NH3 = Ag(NH3)n+ ; bn = [Ag(NH3)n+] / ([Ag+ ][NH3]n)

Expression des concentrations à l'équilibre [Ag(NH3)n+]i et [NH3]i :


avancement (mmol)
Ag+
+ n NH3
= Ag(NH3)n+
initial
0
v0c0 = 0,2
vi
0
en cours
x
0,2 -x
vi -nx
x
équilibre
xéq
0,2 - xéq
vi - nxéq
xéq
volume total (mL) = 100 mL

[NH3]i =( vi - nxéq) / 100 ; [Ag(NH3)n+]i = xéq / 100 ;

or vi >> 0,2 ; (solution d'ammoniac concentrée)

en conséquence : l'excès d'un réactif déplace l'équilibre vers la droite ( sens direct) et la réaction peut être considérée comme totale; de plus il se forme le complexe avec n le plus élevé.

xéq = 0,2 mmol ; [Ag(NH3)n+]i =0,2 / 100 = 2 10-3 mol/L ; [NH3]i =( vi - 0,2 n) / 100 proche de 0,01vi mol/L avec vi en mL.

On réalise la pile de concentration suivante pour chaque solution Si :

Expression de la formule de Nernst pour le couple Ag+/Ag : Ag+/+ e- =Ag

E = E°(Ag+/Ag) + 0,06 log [Ag+].

pour la solution S0 : E0 = E°(Ag+/Ag) + 0,06 log [Ag+]0.

pour la solution Si : Ei = E°(Ag+/Ag) + 0,06 log [Ag+]i.

DEi= Ei-E0 = 0,06 log ( [Ag+]i / [Ag+]0)

DEi est négatif car dans la solution Si, l'ion argent est sous forme complexe. [Ag+]i < [Ag+]0.

avec [Ag+]0 = c0/5 = 2,0 10-3 mol/L ;

bn = [Ag(NH3)n+]i / ([Ag+ ]i[NH3]in) soit [Ag+]i = [Ag(NH3)n+]i / (bn[NH3]in) voisin de 2 10-3/(bn(0,01 vi)n)

DEi= -0,06 log (bn(0,01 vi)n) = -0,06 log bn - 0,06n log (0,01 vi)

DEi permet de déterminer les valeur de n et bn : on trace la droite d'équation DEi= f(log (0,01 vi)

vi(mL)
20
40
60
log (0,01 vi)
-0,7
-0,4
-0,22
DEi(mV)
-342
-374
-392

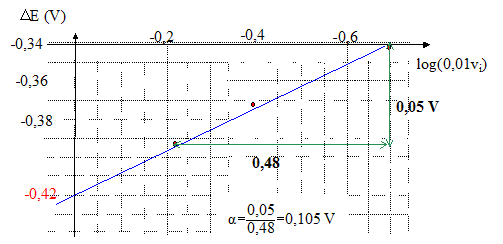
le coefficient directeur donne : 0,06n =0,105 et l'ordonnée à l'origine donne -0,06 log bn = -0,42 V

d'où n = 0,105/0,06 = 1,73 ( n étant entier, on prend n= 2) et log bn = 0,42/0,06 = 7 ; bn =107.

La constante de formation du complexe ammine argent (I) a pour valeur b1 = 103,4.

Montrons que dans les conditions de l'expérience on peut négliger la formation de ce complexe

b1 = [Ag(NH3)+]i / ([Ag+ ]i[NH3]i) ; [Ag(NH3)+]i = b1[Ag+ ]i[NH3]i

avec [Ag+ ]i = 2 10-3/(b2(0,01 vi)2) = 2 10-6 / vi2 ; [NH3]i = 0,01 vi ;

[Ag(NH3)+]i = 103,4* 2 10-8 / vi = 2 10-4,6 / vi =5 10-5 / vi.

on trouve des valeurs voisines de 10-6 mol/L , alors que [Ag(NH3)2+]i = 2 10-3 mol/L.

retour -menu