|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
Le travail d'une force est un mode de transfert d'énergie.
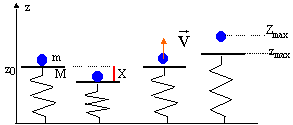 Les questions suivantes sont indépendantes.
Mg
+ mg = k(l0-z0) (1) Dans la situation en (b) : L'énergie du système {ressort, plateau, masse m} est sous forme potentielle élastique et de pesanteur, la longueur du ressort étant z0-X, l'altitude du centre d'inertie de la masse et du plateau étant -X. Em = ½k ( z0-X-l0)² + (M+m)g(-X) Dans la situation en (c) : l'énergie de ce système est sous forme cinétique : Em = ½(M+m) V² l'énergie mécanique se conserve : ½k ( z0-l0-X)² - (M+m)g X = ½(M+m) V² V²
=k ( z0-l0-X)² / (M+m)-2gX
énergie mécanique juste avant décollage : ½mV². énergie mécanique au point le plus haut ( vitesse nulle) = énergie potentielle de pesanteur = mg Zmax. conservation de l'énergie mécanique : ½mV² = mgZmax Zmax
=½ V² / g.
énergie mécanique à l'instant où la masse m décolle : ½MV². énergie mécanique au point le plus haut (vitesse nulle) : ½k(zmax-l0)²+Mg(zmax-z0). conservation de l'énergie mécanique : ½MV² = ½k(zmax-l0)²+ Mg(zmax-z0).
3 . Le travail des forces mécaniques, entraînant le rotor d'une dynamo ou d'un alternateur produit de l'énergie électrique. Exemple : Un cycliste délivre sur un vélo une puissance P= 300 watts. Il maintient ce rythme pendant 10 minutes. La dynamo ( générateur électrique) de son vélo a un rendement de 80%. L'énergie fournie par la dynamo est-elle suffisante pour charger un accumulateur ( résistance interne nulle) afin que l'on puisse faire fonctionner pendant 15 min une lampe de 60 W. corrigé Energie mécanique ( J) fournie par le cycliste en dix minutes = puissance (W) * durée ( seconde) 100*10*60 = 60 000 J La dynamo reçoit cette énergie mécanique et en convertit 80 % en énergie électrique ; l'énergie électrique obtenue vaut : 60 000*0,8 = 48000 J L'énergie électrique consommée par la lampe pendant 15 min vaut : puissance (W) * durée (s) = 60*15*60 = 54 000 J Cette valeur étant supérieure à l'énergie électrique disponible aux bornes de l'accumulateur, la lampe ne peut pas fonctionner pendant 15 min. La durée de fonctionnement de la lampe sera : 48000 / 60 = 800 secondes ( 13 min et 30 s).
4 . Le travail des forces de frottement, lors d'un freinage, transfert aux freins de l'énergie thermique. Exemple : Un frein à disque se compose d'une partie fixe : l'étrier, solidaire des structures du véhicule, et d'une partie mobile : le disque, entraîné par la roue. L'étrier supporte les deux plaquettes qui, sous l'action d'une commande généralement hydraulique, pressent le disque, empêchant ainsi sa rotation. Les plaquettes sont toujours maintenues en léger contact ou à très courte distance (0,20 à 0,25 mm) du disque. Ce sont les plaquettes qui entrent en contact avec le disque de frein et freinent le véhicule. Leur garniture peuvent être en métal fritté (sinter) ou en organique (céramiques). Les plaquettes se distinguent en fonction de leur utilisation et de leur température de fonctionnement habituel : Plaquettes " route " entre 80° et 300° ; Plaquettes " sport " entre 150° à 450° ; Plaquettes " racing " entre 250 et 600°. Les plaquettes ne sont réellement efficaces qu'une fois arrivé à leur température de fonctionnement. Comme il est rare d'atteindre 250°C sur route, des plaquettes " racing " seront moins efficaces que des " routes " pour une utilisation quotidienne.
Une automobile de masse M= 900 kg roule à une vitesse de
50 km.h-1. L'automobiliste freine brusquement et
s'arrête au bout de 40 m . Calculer la quantité d'énergie transférée au
niveau des freins. corrigé Les freins permettent de transformer l'énergie cinétique du véhicule en énergie interne des pièces de freinage. Le transfert d'énergie entre le disque et les plaquettes est dû au travail des forces de frottement. La quantité d'énergie transférée au niveau des freins correspond à la variation d'énergie cinétique du véhicule : vitesse en m/s : 50 / 3,6 = 13,89 m/s DEc = Ecf - Eci = 0 - ½ mv² = - ½ * 900 * 13,89² = - 8,68 104 J Cette énergie correspond à la variation d'énergie interne des freins, l'énergie reçue par les freins est : D U = - D Ec = 8,68 104 J Si toute cette énergie était fournie à une masse m = 1 kg d'eau pour la chauffer, la variation de son énergie interne serait : D U = m c D q soit D q = D U /( m c )=8,68 104 / 4180 = 20,7 ° C .
|
|
|
On étudie une toute petite partie de l'univers : celle-ci est appelée "système ". Le reste de l'univers constitue le milieu extérieur.
|
||
|
corrigé énergie thermique absorbée par le glacon lorsque sa température passe de -8°C à 0 °C : Q = m c( qf - qi ) = 0,02 * 2100*(0-(-8)) = 336 J. A 0°C, la glace fond ( fusion). énergie thermique absorbée par un glacon pendant son changement d'état physique : Q = m L= 0,02 * 335000 = 6700 J. |
||
|
|