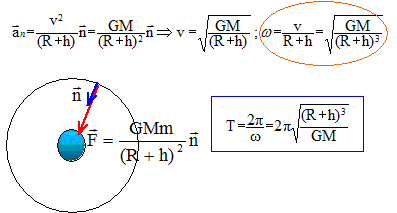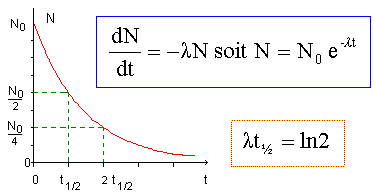Aurélie 15/3/06

d'après concours officier 1ère classe marine marchande 2005

accélération, satellite, polonium, condensateur, cinématique, circuit rLC

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


accélération (2pts)

  1. Représenter l'allure du vecteur accélération aux points M, N, P, Q, R. Les durées des parcours AB, BC, CD, DE et EF sont identiques.
  2. Un véhicule de masse m=1,3 t roule à une vitesese v=72 km/h sur une portion rectiligne. Calculer son énergie cinétique.
  3. Devant le véhicule de la question précédente, la route fait un coude à angle droit. Le véhicule freine sur une distance L jusqu'à s'immobiliser juste avant le coude. La force de freinage f est supposée constante. Etablir son expression.
  4. Si au lieu de freiner le conducteur décide d'entamer une giration circulaire à vitesse constante, de rayon r, exprimer la force centripète que subit le véhicule. Le virage est relevé d'un angle a.
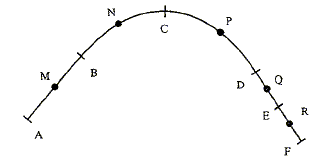
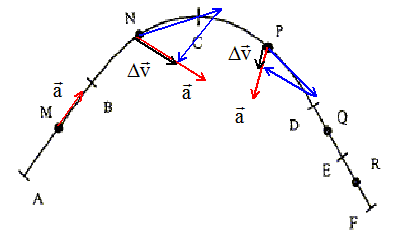
corrigé
Le vecteur accélération est égale à la dérivée du vecteur vitesse par rapport au temps. Le vecteur vitesse est porté par la tangente à la trajectoire et à le sens du mouvement.

AB : variation du vecteur vitesse et donc accélération sont portés par la droite (AB). Si la vitesse diminue, le vecteur accélération est dirigé de B vers A ; si la vitesse augmente, le vecteur accélération est dirigé de A vers B.

En N et P, on a construit le vecteur variation de vitesse.

DE et EF : les distances parcourues pendant des durées égales sont égales ; la trajectoire est rectiligne : mouvement rectiligne uniforme, donc accélération nulle.

énergie cinétique : Ec= ½mv² avec m = 1300 kg et v= 72/3,6 = 20 m/s

Ec= 0,5*1300*20² =2,6 105 J.

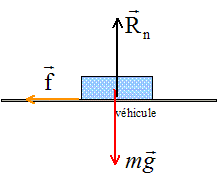
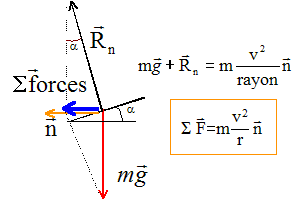
Poids et Rn perpendiculaires à la vitesse, ne travaillent pas. Le travail des frottements est résistant : W= -f L

La somme des travaux des forces est égale à la variation de l'énergie cinétique : 0-½mv²=-f L d'où f = mv²/(2L).


satellite artificiel : (2 pts)

On conssidère la Terre comme une sphère homogène de centre O, de rayon R et de masse M. Un satellite artificiel, de masse m, décrit une orbite circulaire dans le plan de l'équateur, à l'altitude h. On s'intèresse à la vitesse v du satellite dans le référentiel géocentrique.

  1. Donner la définition du référentiel géocentrique.
  2. Exprimer la vitesse angulaire w du satellite en fonction de M, R, h et G, constante de gravitation.
  3. En déduire la période de révolution du satellite.
corrigé
référentiel géocentrique : solide formé par le centre de la terre et par les centres de 3 étoiles lointaines ; l'origine du repère est le centre de la Terre ; les trois axes pointent vers des étoiles lointaines qui paraissent fixes.


radioactivité (4 points)

Un échantillon est constitué de 150 mg de polonium instable 21084Po. qui se transforme en 20682Pb.

Données : demi vie du polonium : t½= 138,3 jours. M(Po) = 210 ; M(Pb) = 206 g/mol. NA= 6,02 1023 mol-1.

  1. Nommer les particules correspondants aux nombres 210 et 84 pour le polonium. Combien de neutrons contient le noyau de polonium ?
  2. Écrire la réaction de désintégration du noyau de polonium. Quelle est la nature de la particule émise ? Quel est le type de radioactivité ?
  3. Calculer le nombre d'atomes de polonium présents dans l'échantillon neuf.
  4. Donner l'expression de la loi de décroissance radioactive. Quelle est la constante de temps t ?
  5. Donner la définition de l'activité radioactive. Quelle est sa valeur pour l'échantillon de polonium neuf ?
  6. Au bout de combien de temps l'activité est-elle égale au 1/8 ème de sa valeur initiale ? Quelle est la masse de plomb formée ?
corrigé
particules correspondants aux nombres 210 et 84 pour le polonium : 84 protons ; 210 nucléons soit 210-84 = 126 neutrons

21084Po --> 20682Pb + 42He émission d'un noyau d'hélium ou particule a.

nombre d'atomes de polonium présents dans l'échantillon neuf :

m(g) / M(g/mol) * NA =0,15/210*6,02 1023 = 4,3 1020.

loi de décroissance radioactive :

constante de temps t = 1/l avec l =ln2 / t½=ln2 / (138,3*24*3600)= 5,8 10-8 s-1 ; t = 1,72 107 s.

activité radioactive : notée A, nombre moyen de désintégrations par seconde, exprimée en becquerel ( Bq)

A= l N = 5,8 10-8*4,3 1020 = 2,5 1013 Bq.

l'activité est-elle égale au 1/8 ème de sa valeur initiale à la date : t = 3 t½ = 3*138,3 = 415 jours.

à chaque période t½, l'activité est divisée par deux.

A chaque noyau de polonium désintégré correspond la formation d'un noyau de plomb ; 87,5% des noyaux de polonium ont disparu

soit 0,875*4,3 1020 =3,76 1020 noyaux. Il s'est formé 3,76 1020 noyaux de plomb ou 3,76 1020 / NA= 6,25 10-4 mol de plomb

masse de plomb formé : 6,25 10-4*206 = 0,129 g = 129 mg.

capacité et énergie (3 points)

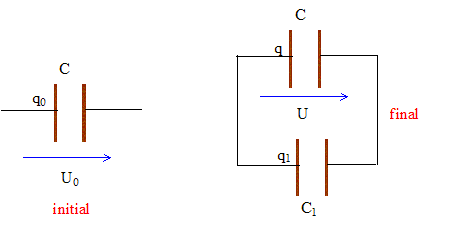
Soit un condensateur de capacité C= 2,7 mF ; la tension à ces bornes est 1000 V. Ce dernier est relié à un condensateur non chargé de capacité C'= 1 m F.

  1. Calculer la charge initiale.
  2. Calculer la tension aux bornes de l'ensemble, l'équilibre étant atteint.
  3. Calculer l'énergie finale du système.
  4. Calculer la perte d'énergie qui a lieu lors du branchement et conclure.
corrigé
charge initiale : q0 = C U0= 2,7 10-6*1000 = 2,7 10-3 C

énergie initiale stockée : 0,5 CU02=0,5*2,7 10-6 *106=1,35 J

La charge totale n'a pas changée : q0 = q+q1.

capacité équivalente à l'ensemble : C= 2,7 + 1 = 3,7 m F.

tension finale U=q0 /C=2,7 10-3 /3,7 10-6 = 730 V.

énergie finale stockée : 0,5*3,7 10-6*7302= 0,98 J.

pertes d'énergie : 1,35-0,98 = 0,37 J.

perte d'énergie par rayonnement électromagnétique et par effet joule dans les conducteurs lors de l'association.

cinématique (4 points)

Une barre de cuivre MN homogène, de masse M, de longueur L peut glisser sans frottements sur deux rails rectilignes AC et A'C' contenus dans un plan incliné d'un angle a=30° par rapport à l'horizontale. Pendant tout le mouvement la barre reste perpendiculaire aux rails et le contact est maintenu. La barre MN est lâchée sans vitesse initiale.

  1. En admetant l'existence d'une force de frottement constante f, faire le bilan des forces agissant sur la barre.
  2. Déduire la nature du mouvement.
  3. Quelle est la relation liant la vitesse de la barre et la distance parcourue ?
  4. La force de frottement est maintenant proportionnelle à la vitesse. Etablir l'équation différentielle correspondant à la vitesse.
  5. Quelle est la vitesse limite de la barre.
corrigé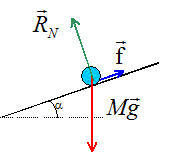

poids Mg, action normale du plan Rn, frottement f .

Ecrire la seconde loi de Newton suivant un axe parallèle au plan et orienté vers le bas : Mg sin a - f = Ma

d'où a = g sin a - f /M ( constante) : le mouvement est uniformément accéléré si g sin a > f /M

si g sin a < f /M, la barre reste immobile.

relation liant la vitesse de la barre et la distance parcourue :

écrire le thèorème de l'énergie cinétique pour une descente de longueur L: S travaux des forces = DEc.

DEc = ½Mv²-0 = ½Mv² ; travail des frottement : -f L; travail moteur du poids en descente : MgL sin a.

½Mv² = L( Mg sin a - f) ; v² = 2L(g sin a - f /M)

équation différentielle correspondant à la vitesse : valeur de f = k v avec k = constante et a = dv/dt

d'où : Mg sin a -kv = Mdv/dt ; dv/dt + k/M v =gsin a.

vitesse limite de la barre :

Lorsque la vitesse limite est atteinte le mouvement est rectiligne uniforme et dvlim /dt = 0

k/M vlim = gsin a ; vlim =Mg sin a / k.

cirduit rLC (5 points)

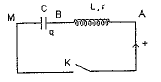
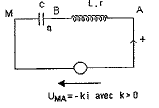
On considère le circuit LC suivant :

 

Le condensateur de capacité C est initialement chargé ( Q0= 4,7 10-6 C). A la fermeture de l'interrupteur il est relié à une bobine inductive d'inductance L et de résistance r.

  1. Etablir l'équation différentielle décrivant l'évolution temporelle de la charge q du condensateur.
  2. En négligeant r, calculer la période propre et la fréquence des oscillations électriques.
  3. Les oscillations ne sont pas entretenues et on tient compte de la résistance du circuit. Donner une interprétation énergétique de l'allure des oscillations électriques observées.
    - Nommer un dispositif permettant d'entretenir les oscillations électriques.
  4. On introduit le dispositif suivant :
    - Etablir la nouvelle équation différentielle et en déduire une relation entre r et k pour que les oscillations soient entretenues.
    C= 0,47 mF ; L= 5,6 mH ; r= 0,2 W.

 

corrigé
équation différentielle décrivant l'évolution temporelle de la charge q du condensateur : additivité des tensions : uAB+uBM=0

uAB=Ldi/dt + r i ; uBM= q/C ; de plus i = dq/dt = q' ; di/dt = d2q/dt2= q''

Ldi/dt + r i + q/C = 0 ; L q'' + r q' +q/C=0 ; q'' + r/L q' + q/(LC)=0 ; on pose w2=1/ (LC) ; q" + r/L q' + w2 q=0 (1)

période propre et la fréquence des oscillations électriques : T= 2p(LC)½ = 6,28 (5,6 10-3*4,7 10-4)½=0,010 s ; f= 1/0,01 = 100 Hz.

Les oscillations ne sont pas entretenues et on tient compte de la résistance du circuit. Interprétation énergétique de l'allure des oscillations électriques observées : au cours des échanges d'énergie entre condensateur et bobine inductive, une partie de l'énergie est perdue sous forme d'effet joule dans les résistances électriques. L'amplitude de la grandeur visualisée diminue à chaque période.
Dispositif permettant d'entretenir les oscillations électriques : il faut compenser à chaque instant l'énergie perdue ; utiliser un dispositif électronique simulant une résistance négative.

nouvelle équation différentielle :

uAB+uBM+ uMA=0

uAB=Ldi/dt + r i ; uBM= q/C ; uMA= -k i

Ldi/dt + r i + q/C -k i=0 ; Lq" +(r-k)q' +q/C=0

relation entre r et k pour que les oscillations soient entretenues : r= k.

retour -menu