Aurélie 05/06

Mouvement d'une balle de tennis

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Mouvement d'une balle de tennis

Un joueur de tennis ( joueur 1) désire effectuer un lob, cela signifie qu'il doit envoyer la balle suffisamment haut pour que son adversaire ( joueur 2) ne puisse pas l'intercepter. La balle doit retomber dans les limites du court.

On notera A le point où le joueur 1 frappe la balle, O comme origine du repère. OA= z0 = 1,00 m, ordonnée de A ; z1 = 3,00 m ordonnée correspondant à la hauteur maximale pour laquelle le joueur 2 peut intercepter la balle quand il lève sa raquette. x1 = 15,0 m, abscisse correspondant à la position du joueur 2.; x2 = 25,0 m , abscisse correspondant à la ligne de fond du court du joueur 2. v0 vitesse initiale de la balle en A ; a= 45,0° ; g=9,80.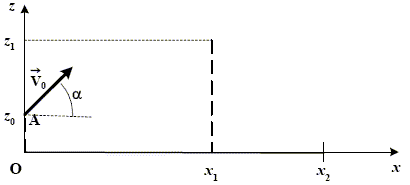

Pour que le lob soit réussi, il faut donc que la balle issue de A avec la vitesse initiale v0 soit telle que z>z1 pour x=x1 et que x<x2 pour z=0. On se propose se déterminer les valeurs de la vitesse initiale v0 pour que le lob soit réussi. On néglige tous les effets liés à l’air.

  1. Compte tenu des hypothèses, quel est le nom mathématique de la courbe décrite par la trajectoire de la balle ?
  2. Donner les expressions littérales des composantes du vecteur vitesse initiale.
  3. Donner les expressions littérales des équations horaires x(t) et z(t).
  4. Donner l’expression littérale de la trajectoire z(x).
  5. A partir de l’équation précédente, exprimer la vitesse initiale v0 en fonction de x, z, z0, a et g.
  6. En déduire la valeur numérique v0 1 de la vitesse initiale pour que la balle touche le sol au point de coordonnées : x = x1 z = z1.
    De même, donner la valeur numérique v0 2 de la vitesse initiale pour que la balle touche le sol au point de coordonnées : x = x2 z = 0.
    En déduire finalement l’intervalle de la valeur de la vitesse initiale pour lequel le lob est réussi.

corrigé
nom mathématique de la courbe décrite par la trajectoire de la balle : arc de parabole

expressions littérales des composantes du vecteur vitesse initiale :

sur Ox : v0x= v0 cos a ; sur Oz : v0z = v0 sin a.

expressions littérales des équations horaires x(t) et z(t) : composantes de l'accélération : ax=-g ; az=0 ; position initiale : x0 = 0 ; z0 = OA

la vitesse est une primitive de l'accélération : vx= v0x= v0 cos a ; vy = -gt +v0 sin a.

Le vecteur position est une primitive deu vecteur vitesse : x= v0 cos a t ; z = -½gt² + v0 sin a t + z0 .

expression littérale de la trajectoire z(x) : t =x/( v0 cos a ) ; repport dans z :

z= -½gx²/( v0 cos a )² + x tan a + z0.

expression de vitesse initiale v0 en fonction de x, z, z0, a et g :
-z+ z0 +x tan a = ½gx²/( v0 cos a )² ; v0² = ½gx² /((-z+ z0 +x tan a)cos² a)

v0 = [ ½gx² /((-z+ z0 +x tan a)cos² a)]½.

valeur numérique v0 1 de la vitesse initiale pour que la balle touche le sol au point de coordonnées : x = x1 z = z1 :

v0 1 =[ ½gx1² /((-z1+ z0 +x1 tan a)cos² a)]½ = [4,9*15²/((-3+1+15)*0,5]½ =[4,9*225/6,5]½ =13,0 m/s.

valeur numérique v0 2 de la vitesse initiale pour que la balle touche le sol au point de coordonnées : x = x2 z = 0 :

v0 2 =[ ½gx2² /((-z2+ z0 +x2 tan a)cos² a)]½ = [4,9*25²/((1+25)*0,5]½ =[4,9*625/13]½ =15,3 m/s.

intervalle de la valeur de la vitesse initiale pour lequel le lob est réussi : [13,0 ; 15,3 m/s]

retour -menu