Aurélie 10/04/06

Dipôle RL. 

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


dipôle RL

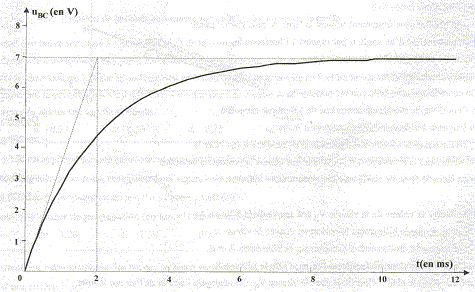
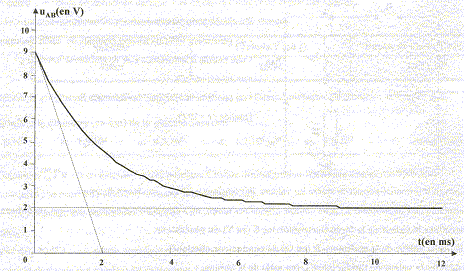
Un circuit est composé d'un générateur de tension continue de fem E, d'une bobine d'inductance L et de résiqtance r= 10 W, d'un interrupteur K et d'un conducteur ohmique R. Un dispositif informatisé permet de suivre les valeurs des tensions uAB et uBC au cours du temps. La fermeture de l'interrupteur est prise comme origine des temps.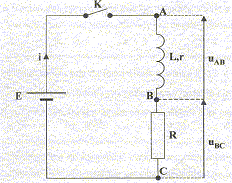

 

  1. Déterminer E.
  2. Calculer R et en déduire L ( en mH).
  3. Donner l'expression littérale de l'intensité i du courant en fonction de L, R , E et r. En déduire la valeur de l'intensité à t= 0,003 s.
  4. Calculer la valeur de l'énergie stockée par la bobine à t = 0,003 s.

corrigé
Déterminer E : uAB + uBC= E avec uBC = Ri et uAB = Ldi/dt + ri

en régime permanent di/dt=0 ; uBC = 7 V ; uAB =2 V soit E = 9 V.

Calculer R et en déduire L : en régime permanent uBC = 7= RI ; uAB =2 = rI soit I= 2/10 = 0,2 A ; R= 7/0,2 = 35 W.

R[di/dt]t=0 = 7/2 10-3 soit [di/dt]t=0 =7/(2R 10-3) = 100 A/s ;

tension aux bornes de la bobine à t=0 : 9= L[di/dt]t=0 =100 L d'où L= 9/100 = 0,09 H = 90 mH

ou bien à partir de la constante de temps t du dipôle qui est égale à 2 10-3 s ( lecture graphe) ; de plus t = L/(R+r)

d'où L= t (R+r) = 2 10-3*45 = 90 mH.

Expression littérale de l'intensité i du courant en fonction de L, R , E et r :

uAB + uBC= E avec uBC = Ri et uAB = Ldi/dt + ri

éq différentielle : E= Ldi/dt + (R+r) i

solution de la forme i(t) = A exp(-(R+r)t /L )+ B

à t = 0 l'intensité est nulle d'où A+B=0 soit B=-A.

en régime permanent ( t <5 t) : 0,2 = B = E/(R+r)

i(t) = E/(R+r)(1-exp(-(R+r)t /L ) = 0,2(1- exp(- t/2 10-3))

i(0,003) = 0,2 (1-exp (-1,5)) =0,155 A. (155 mA)

valeur de l'énergie stockée par la bobine à t = 0,003 s :

½Li² = 0,5*0,09*0,155² = 1,1 10-3 J = 1,1 mJ.

retour -menu