|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
I. Diapason : Un diapason émet un son pur d'une seule fréquence. L'intensité de ce son est amortie au cours du temps. On place un microphone devant le diapason et on enregistre la tension recueillie aux bornes d'un microphone grâce à un dispositif adapté.
II. Sonomètre : On place maintenant un sonomètre à une distance d1 du diapason précédent. Lorsque le diapason est en train d'émettre un son, à un instant donné t, le sonomètre indique 80 dB.
Intensité minimale audible I0 = 10-12 Wm-2. corrigé 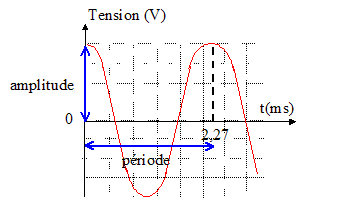
la période est l'inverse de la fréquence : T=1/440 = 2,27 ms longueur d'onde (m) = célérité (m/s) / fréquence (Hz) = 340/440=0,773 m. pour parcourir 50 m à
la célérité c=340 m/s, le son met : 50/340 = 0,147 s.
intensité acoustique pour plusieurs diapason, s'ajoutent : Itotal= I0 108,6 = 10-12*108,6 = 10-3,4 = 4 10-4 W/m². cete intensité
correspond à 4 diapasons jouant simultanément.
à la distance d1 : P=4pd1²I1 ; à la distance d2: P=4pd2²I2 ; d'où d1² I1 = d2² I2 soit : I1 /I2 = (d2/d1)2. de plus le niveau sonore (dB) s'exprime par : N1= 10 log (I1/I0) et N2= 10 log (I2/I0) atténuation (dB) :A= N1-N2
= 10 log (I1/I0) -10 log
(I2/I0) = 10 log(I1
/I2) = 10 log( (d2/d1)2)
= 20 log(d2/d1)
A=80-65 = 15 dB ; 15/20 =0,75 = log(d2/d1) ; d2/d1= 100,75 =5,62 soit d2 = 5,62 d1=5,62*5 = 28 cm.
|
|
|
Un caisson hermétiquement fermé est rempli d'air, considéré comme un gaz parfait. Ce saisson a les dimensions suivantes :longueur L= 120,0 cm ; largeur l= 80,0 cm ; hauteur h= 90,0 cm.
Masse molaire de l'air : 29,0 g/mol corrigé 
équation aux dimensions relative à la loi des gaz parfaits : pression = force / surface ; une force est une masse fois une accélération : pression = masse * accélération / surface Une accélération est une longueur divisée par un temps2 : pression = masse * longueur / (temps2 * longeur2) = masse / (temps2 * longeur) = M T-2L-1. volume : longueur3 = L3. d'où [PV] = M T-2L2. température : q ; quantité de matière N [R]= [PV/(nT)]= M T-2L2 N-1q-1. unité J mol-1 K-1. quantité de matière n1 d'air du caisson n1 = PV/(RT) volume V= L l h = 1,2*0,8*0,9 =0,864 m3 ; T=273+25 = 298 K n1 = 1,013 105*0,864/(8,31*298)=35,34 mol = 35,3 mol. nouvelle pression P2= n1RT2/V =35,34*8,31*(273+40)/0,864 =1,06 105 Pa. quantité de matière d'air dans le caisson sous la pression P1, à la température T2 : n= P1V/(RT2)=1,013 105*0.864/(8,31*313)=33,65 mol Qté de matière d'air ayant disparu du caisson: 35,34-33,65 =1,69 mol. masse d'air (g) = quantité de matière (mol) * masse molaire (g/mol) = 1,69*29 =49,0 g. |
||
|
I. On considère deux récipients A et B. Le récipient A contient un volume VA d'une solution aqueuse d'acide chlorhydrique ( H3O+(aq); Cl-(aq) de concentration molaire CA. Le récipient B contient un volume VB d'une solution aqueuse d'hydroxyde de potassium ( K+(aq); HO-(aq) de concentration molaire CB.
II. Le butane est utilisé comme combustible.
C:12,0 ; H : 1,00 ; O : 16,0 g/mol. corrigé Je calcule une concentration molaire (mol/L) en divisant une quantité de matière (mol) par le volume de la solution (L). nA = CA VA=0,5*0,6 = 0,3 mol. nB = CB VB=1,3*0,8 = 1,04 mol. quation-bilan de la réaction qui se produit H3O+ + HO- = 2H2O 0,3 mol d'ion oxonium réagit avec 0,3 mol d'ion hydroxyde : il reste 1,04-0,3 = 0,704 mol d'ion hydroxyde dans 1,4 L de solution. [HO-]=0,704/1,4 = 0,50 mol/L Or [H3O+][HO-]=10-14 d'où [H3O+] = 10-14 / HO-] = 2 10-14mol/L pH= - log [H3O+]
= - log 2 10-14= 13,7.
masse molaire du butane : 4*12+10 = 58 g/mol Quantité de matière de butane = masse (g) / masse molaire (g/mol) = 200/58 = 3,45 mol. d'où : quantité de matière CO2 : 4*3,45 = 13,8 mol ; quantité de matière d'eau : 5*3,45 = 17,2 mol. masse molaire CO2 : 12+2*16 = 44 g/mol masse CO2 : quantité de matière (mol) * masse molaire (g/mol)= 13,8*44 = 607 g. masse molaire H2O: 2+16 = 18 g/mol masse d'eau : 17,2*18 = 310 g.
|
||
|
|