Aurélie 28/11/05

Eolienne : étude hydraulique ; acoustique ; combustion du diesel d'après bts EEC 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


étude hydraulique ( 7,5 points)

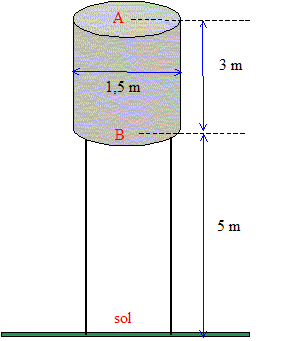
Un projet consiste à faire pousser des cultures par irrigation sur une ile où l'eau douce n'est accessible qu'en prfondeur par pompage. Pour cela, trente éoliennes vont être mise en place, groupées sur une zône ventée à 1 km de la première habitation. Ces éoliennes arrivent par bateau. Une éolienne de pompage se présente de la façon suivante :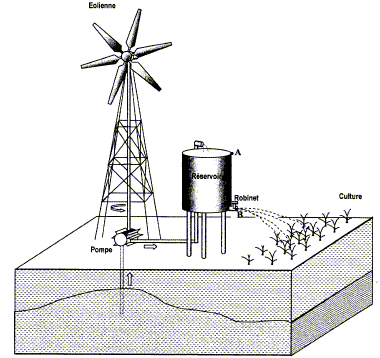

Le réservoir associé à chaque éolienne est ouvert ( pour récupérer éventuellement l'eau de pluie). Il a pour dimensions 1,5 m de diamètre et 3,0 m de hauteur. Son fond est situé à une hauteur de 5,0 m au dessus du sol. Une fois les réservoirs pleins, les pompes sont arrêtées. L'eau va être utilisée pour l'irrigation.

  1. Sachant que les cultures consomment 2 L par plant par jour, qu'il y a 5000 plants, combien de temps les trentes réservoirs des éoliennes permettent-ils de tenir sans pluie, ni vent ?
  2. Dans la suite on restreint l'étude à un seul réservoir. Faire un schéma du réservoir en précisant les dimensions et les hauteurs par rapport au sol.
    - Le réservoir étant plein et le robinet fermé, calculer la pression PB due au seul liquide en B au niveau du robinet situé en bas du réservoir.
  3. On ouvre le robinet. Préciser les pressions en haut du réservoir ( A) et au niveau du robinet ouvert à l'air libre ( B)
    - On considère le réservoir suffisamment grand pour que l'eau soit considérée comme stagnante dans le réservoir ( vA=0). En utilisant la relation de Bernoulli, calculer la vitesse d'écoulement vB de l'eau à la sortie du robinet.
    - En déduire le débit volumique Qv sachant que le diamètre du robinet est de 40 mm.
  4. En supposant le débit constant et sa valeur égale à celle calculée précédemment, quel serait le temps mis pour vider complétement le réservoir ?
    - Le temps réel est-il inférieur ou supérieur à cette valeur ? Justifier.

Masse volumique de l'eau r = 1000 kg m-3 ; g = 10 m/s² ; pression atmosphérique P0= 1,0 105 Pa.

 

corrigé
Durée de l'irrigation, sans pluie, ni vent :

Sachant que les cultures consomment 2 L par plant par jour, qu'il y a 5000 plants, le volume d'eau utile chaque jour est : 2*5000 = 10 000 L = 10 m3.

volume d'un réservoir cylindrique : V= pr2h avec r = 0,75 m et h = 3,0 m

V= 3,14*0,752*3 = 5,3 m3

volume des 30 réservoirs : 30*5,3 = 159 m3

d'où la durée : 159/10 voisin de 16 jours.

pression PB due au seul liquide en B au niveau du robinet situé en bas du réservoir :
Le réservoir est plein et le robinet est fermé :

PB = r g AB

PB = 1000 * 10*3 =3,0 104 Pa.

On ouvre le robinet : les pressions en haut du réservoir ( A) et au niveau du robinet ouvert à l'air libre ( B) sont égales à la pression atmosphérique P0= 1,0 105 Pa
vitesse d'écoulement vB de l'eau à la sortie du robinet :

On considère le réservoir suffisamment grand pour que l'eau soit considérée comme stagnante dans le réservoir ( vA=0). La relation de Bernoulli s'écrit :

pA + rgzA +½rvA² = pB + rgzB +½rvB²

p : pression en pascal ; r masse volumique du fluide (eau) kg/m3; z altitude en mètre ; v : vitesse d'écoulement en m/s.

Or pA=pB et zA-zB= 3 et vA=0 d'où : vB² =2 g(zA-zB) = 20*3 = 60 ; vB= 7,7 m/s.
Le débit volumique Qv est égal à la section (m²) fois la vitesse d'écoulement en B :( le rayon du robinet est de 0,02 m )

Qv= pr²vB= 3,14*0,022*7,7= 9,7 10-3 m3/s = 9,7 L/s.

En supposant le débit constant le temps mis pour vider complétement le réservoir est : volume réservoir (m3) / debit volumique (m3/s)

t = 5,3 / 9,7 10-3 = 5,7 102 s.
Le temps réel est supérieur à cette valeur car zA-zB diminue au fur et à mesure de la vidange ; or vB² =2 g(zA-zB) et Qv= pr²vB : en conséquence le débit en B diminue au cours du temps.


acoustique (6,5 points)

Une éolienne en fonctionnement a un niveau d'intensité acoustique L= 60 dB à 10 m. La population la plus proche se trouve à 1 km. On donne le seuil d'audibilité à 1000 Hz : I0 = 1,0 10-12 Wm-2.

  1. Calculer l'intensité acoustique I à 10 m d'une éolienne. En déduire la puissance acoustique d'une éolienne en supposant qu'elle émet de façon homogène dans toutes les directions.
  2. Dans le but d'estimer l'impact acoustique sur la population, l'ingénieur considère la situation fictive correspondant au maximum de nuisance : les trente éoliennes étudiées sont situées toutes au même endroit.
    - Calculer dans ce cas l'intensité acoustique résultante IT à 10 m.
    - Déterminer le niveau d'intensité acoustique LT de ces trente éoliennes à 10 m.
  3. Dans cette hypothèse, à quelle distance faut-il se placer pour avoir le "calme", soit un niveau sonore de 30 dB ?
    - Le niveau sonore mesuré à l'extérieur, à 1 km du site, est LM= 34 dB. Quelle valeur du taux d'affaiblissement TA de la paroi d'une habitation permettrait d'avoir le "calme" à l'intrieur ?

On donne I= W/(4pd²)

 

corrigé
Intensité acoustique I à 10 m d'une éolienne :

L = 10 log ( I/I0) soit I= I0 10 0,1 L = 10-12 * 106 ; I= 10-6 Wm-2.

Puissance acoustique d'une éolienne en supposant qu'elle émet de façon homogène dans toutes les directions :

P= 4pd² I = 4*3,14*102*10-6 = 1,25 10-3 W.

Dans le but d'estimer l'impact acoustique sur la population, l'ingénieur considère la situation fictive correspondant au maximum de nuisance : les trente éoliennes étudiées sont situées toutes au même endroit.
Dans ce cas l'intensité acoustique résultante IT à 10 m vaut : IT = 30 I = 3 10-5 Wm-2.
Le niveau d'intensité acoustique LT de ces trente éoliennes à 10 m est :

LT= 10 log ( IT /I0) = 10 log (3 10-5 / 10-12) = 10 log (3 107) = 75 dB.

Calcul de la distance D où il faut se placer pour avoir le "calme", soit un niveau sonore de 30 dB :

Dans ce cas l'intensité acoustique résultante IT à la distance D vaut : IT = I0 10 0,1 L = 10-12 * 103 = 10-9 Wm-2.

soit pour une seule éolienne : I= IT /30 = 3,33 10-11 Wm-2.
Puissance acoustique d'une éolienne en supposant qu'elle émet de façon homogène dans toutes les directions :

P= 4pD² I soit D² = P/(4pI) = 1,25 10-3 / (4*3,14* 3,33 10-11 )= 3 106 ; D= 1,7 103 m = 1,7 km.

taux d'affaiblissement TA de la paroi d'une habitation permettrait d'avoir le "calme" à l'intrieur :

Le niveau sonore mesuré à l'extérieur, à 1 km du site, est LM= 34 dB.

coef de transmission d'une paroi : T = puissance transmise / puissance incidente

affaiblissement phonique : A = 10 log T

l'affaiblissement phonique est de -4 dB soit log T= A/10 = -0,4 ; T= 10-0,4 = 0,4.

Transport des éoliennes (6 points)

Les trente éoliennes arrivent par bateau en pièces détachées : celui-ci consomme environ 10 tonnes de diesel par jour. Pour atteindre l'ile il doit parcourir la distance de 3000 km à la vitesse moyenne de 20 noeuds.

  1. Montrer que le bateau consomme 33,8 tonnes de diesel pour acheminer tout le matériel sur l'ile.
  2. On considère que le diesel a pour formule C12H26. Quelle est la famille de C12H26 ? Donner son nom
  3. Déterminer la quantité de matière de diesel consommée sur le parcours.
  4. Ecrire l'équation équilibrée de combustion complète de ce composé.
  5. Calculer le volume de dioxygène, mesuré dans les conditions ordinaires, nécessaire pour effectuer la combustion totale de 1,0 L de diesel.
  6. On veut évaluer l'impact de la pollution par le dioxyde de carbone sur l'environnement. Déterminer la masse de dioxyde de carbone rejetée dans l'atmosphère lors du trajet du cargo et préciser à quel phénomène contribue le rejet de CO2.

Données : 1 noeud équivaut à 1852 m h-1 ; préfixe 12 : dodèc ; masse volumique du diesel r = 820 g/L ; volume molaire des gaz dans les conditions ordinaires : Vm=24,2 L/mol ; masse atomique molaire ( g/mol) : H : 1 ; C : 12 ; O : 16 ; N : 14.

corrigé
consommation du bateau :

vitesse du bateau : 1,852*20 = 37,04 km/h

durée du parcours ( h) = distance (km) / vitesse (km/h) = 3000 / 37,04 = 81 heures ou 3,38 jours

consommation : 3,38*10 = 33,8 tonnes de diesel

Le diesel a pour formule C12H26 ( du type Cn H2n+2) famille des alcanes ; son nom : dodécane.

quantité de matière n de diesel consommée sur le parcours :

n= masse (g) / masse molaire M (g/mol) avec M= 12*12+26 = 170 g/mol et m= 33,8*1000 kg = 33,8 * 106 g

n= 33,8 106 / 170 = 2,0 105 mol.

équation équilibrée de combustion complète de ce composé :

C12H26 + 18,5 O2 = 12 CO2 + 13 H2O

volume de dioxygène, mesuré dans les conditions ordinaires, nécessaire pour effectuer la combustion totale de 1,0 L de diesel :

masse (g) de 1 L de diesel : volume (L) * masse volumique (g/L) = 820 g

quantité de matière correspondante (mol) = masse (g) / masse molaire m( g/mol) = 820/170 = 4,8 mol.

d'après les coefficients de l'équation de combustion : n(O2) = 18,5 n(diesel) = 18,5*820/170 = 89,2 mol

Or le volume d'une mole de dioxygène dans les conditions ordinaires vaut 24,2 L, d'où le volume de dioxygène :

24,2*89,2 =2159 L = 2,2 m3.

masse de dioxyde de carbone rejetée dans l'atmosphère lors du trajet du cargo :

d'après les coefficients de l'équation de combustion : n(CO2) = 12 n(diesel) =12*33,8 106 / 170 =2,38 106 mol

masse molaire du CO2 : M= 12+2*16 = 44 g/mol.

masse de CO2 (g) = quantité de matière (mol) * masse molaire (g/mol)

m=2,38 106 *44 =1,0 108 g =1,0 102 tonnes.

Le dioxyde de carbone contribue à l'effet de serre, et donc au réchauffement global.


retour -menu