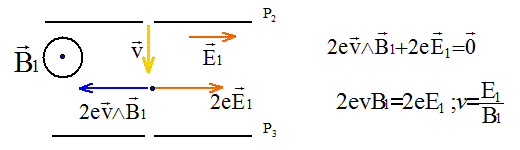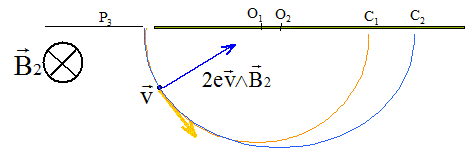Aurélie 16/11/06

étude d'un moteur à combustion interne ; spectrographe de masse d'après bts chimie 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


moteur à combustion interne : cycle de Beau et Rochas

On considère un moteur à combustion interne à allumage par bougies. On se limite à l'étude de l'un des cylindres du moteur. Le cycle thermodynamique décrit par le fluide est le cycle de Beau et Rochas.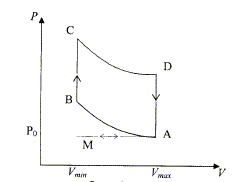

M-A : admission du mélange gazeux air essence à la pression P0. En A il y a fermeture de la soupape d'admission et le volume V est alors égal à Vmax.

A-B compression adiabatique réversible du mélange. Dans l'état B, le volume est égal à Vmini.

B-C : échauffement isochore du gaz.

C-D : détente adiabatique réversible du gaz.
D-A : refroidissement isochore du gaz.
A-M : refoulement des gaz vers l'extérieur à la pression P0.

On convient de nommer "taux de compression" le rapport t=Vmax/Vmin ; ici t=10.

Le système envisagé est le gaz qui décrit le cycle ABCD. La quantité de gaz, n, est celle qui a été admise dans l'état A. L'échauffement de l'étape BC est dû à la combustion "interne" du mélange gazeux admis. Les réactifs et les produits de la réaction sont gazeux. On admettra que la quantité de gaz n'est pas modifiée par la combustion interne.

Le gaz est assimilé à un gaz parfait pour lequel les capacités molaires Cpm et Cvm sont constantes. Cvm = R/(g-1) et g =Cpm/Cvm=1,33.

  1. Soit Q1 la quantité de chaleur échangée dans l'étape B-C. Exprimer Q1 en fonction de n, Cvm, TB et TC. Présicer le signe de cette grandeur.
  2. Soit Q2 la quantité de chaleur échangée dans l'étape D-A. Exprimer Q2 en fonction de n, Cvm, TA et TD. Présicer le signe de cette grandeur.
  3. On note W le travail total échangé au cours du cycle ABCD. Exprimer W en fonction de Q1 et Q2.
  4. Définir l'efficacité h du moteur. Exprimer h en fonction de Q1 et Q2.
  5. A l'aide des relations relatives aux transformations adiabatiques, exprimer h en fonction de TA, TB, TC et TD, puis montrer que l'efficacité peut se mettre sous la forme h = 1-t1-g. Calculer h.
  6. La cylindrée Cy du moteur est égale à 2,0 L. On raisonnera sur un seul cylindre, possédant la cylindrée Cy du moteur définie selon : Cy= Vmaxi-Vmini. Le mélange air essence est admis à la température TA= 320 K sous la pression PA= 100 kPa. La proportion de carburant est de 1/60 en moles.
    - Calculer Vmaxiet Vmini.
    - Calculer la quantité de gaz n' ( mol) de carburant consommée par le cycle. On prendra R= 8,31 J mol-1 K-1.
corrigé
Expression de Q1 quantité de chaleur échangée dans l'étape B-C :

Q1 = nCvm( TC - TB ) avec ( TC - TB )>0 échauffement du gaz

Q1 >0, chaleur reçue par le système, le gaz.

Expression de Q2 quantité de chaleur échangée dans l'étape D-A :

Q2 = nCvm( TA - TD ) avec ( TA - TD )<0 refroidissement du gaz

Q2 <0, chaleur cédée par le système, le gaz.

Expression du travail total W échangé au cours du cycle ABCD :

l'énergie interne du gaz ne varie pas au cours du cycle : DU=0

Or DU=W+ Q1 +Q2 d'où W= -(Q1 +Q2)

Expression de h en fonction de Q1 et Q2.

efficacité ( rendement) : |travail fourni |/ énergie reçue à la source chaude ; h = |W|/Q1 = |-(Q1 +Q2)|/Q1 =|-(1+Q2/Q1 )|

or Q1>0 et Q2<0 d'où h =1-|Q2| /Q1

expression de h en fonction de TA, TB, TC et TD :

|Q2| /Q1 = | TA - TD | / ( TC - TB ) ; h = 1- | TA - TD | / ( TC - TB )

A-B adiabatique d'onc : TAVg-1maxi =TBVg-1mini (1) ; C-D adiabatique d'onc : TDVg-1maxi = TCVg-1mini (2)

(1) -(2) donne : (TA - TD )Vg-1maxi = ( TB - TC )Vg-1mini ;

(TA - TD )/ ( TB - TC ) = Vg-1mini / Vg-1maxi = (Vmini / Vmaxi)g-1 = t1-g

h = 1- t1-g = 1-10-0,33 = 0,53.

La cylindrée Cy du moteur est égale à 2,0 L. On raisonnera sur un seul cylindre, possédant la cylindrée Cy du moteur définie selon : Cy= Vmaxi-Vmini. Le mélange air essence est admis à la température TA= 320 K sous la pression PA= 100 kPa. La proportion de carburant est de 1/60 en moles.

Calcul de Vmaxi et Vmini :
"taux de compression" t=Vmax/Vmin =10 ;Vmax = 10 Vmin ;

Vmaxi-Vmini = 2 soit 9 Vmin = 2 ; Vmin =2/9 = 0,22 L ; Vmaxi = 2,22 L.

Calcul de la quantité de gaz n' ( mol) de carburant consommée par le cycle :

Relation des gaz parfaits pour l'état A : PAVmaxi = n RTA ;

n= PAVmaxi /(RTA) = 105*2,22 10-3 / (8,31*320)=8,36 10-2 mol

n'= n/60 = 1,4 10-3 mol.


Spectrographe de masse

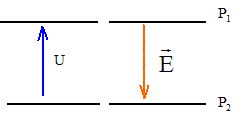
On négligera les effets de la pesanteur devant les autres actions ; la masse des électrons est négligeable devant la masse des ions.

On considère des plaques P1 et P2 parallèles, situées à une distance "d "l'une de l'autre. Une différence de potentielle constante U est appliquée entre P1 et P2.

  1. Des ions positifs de masse m et de charge q sont émis par une source ( située en F1), normalement à la plaque P1, avec une vitesse initiale considérée comme nulle.
    - Préciser qualitativement quelle est la plaque de potentiel le plus élevé et représenter sur un schéma le vecteur champ électrique E.
    - Etablir l'expression littérale de la vitesse v0 des ions qui arrivent sur la plaque P2.
  2. La source émet maintenant, toujours avec une vitesse initiale nulle, des ions positifs de mercure 20080Hg2+ et 20280Hg2+.
    - Calculer v1 et v2 pour ces deux types d'ions arrivant sur la plaque P2. e= 1,6 10-19 C ; masse d'un nucléon = 1,67 10-27 kg ; U= 1,0 104 V ; d = 1,0 m
    Ces ions traversent ensuite la plaque P2 par la fente F2, le vecteur vitesse des ions étant ortogonal à P2. Ils pénètrent dans l'espace séparant P2 et P3 où règnent : - un champ électrique uniforme de valeur E1, parallèle à P2 et à P3, dans le plan de la feuille ; - un champ magnétique uniforme de valeur B1, perpendiculaire au plan de la feuille.
    - Démontrer que seuls parviennent au point F3 ( situé dans le prolongement de F1 et F2) les ions dont la vitesse est v= E1/B1. Préciser l'isotope du mercure qui rempli ces conditions. E1 = 5,3 104 V et B1 = 0,383 T.
    La valeur de B1 restant constante, on règle la valeur de E1 pour permettre le passage de l'autre ion. Au dela de F3, les ions pénèttrent dans une région où ne règne qu'un champ magnétique uniforme de valeur B2, normal au plan de la feuille.
    - Quel doit être le sens de ce champ pour que les ions puissent atteindre O1 ou O2 ?
    - Montrer que le mouvement d'un ion dans cette région est uniforme.
    - Démontrer que la trajectoire est un cercle et vérifier que son rayon vaut R= m1v1/(q1B2).
    - Calculer la distance d=O1O2.
    - Les quantités d'électricité reçues en une minute par les collecteurs C1 et C2 sont respectivement Q1= + 1,20 10-7 C et Q2= 3,5 10-8 C ; déterminer la composition du mélange d'ions. B2 =0,200 T.
corrigé
Des ions positifs de masse m et de charge q sont émis par une source ( située en F1), normalement à la plaque P1, avec une vitesse initiale considérée comme nulle.

Les ions positifs pourront atteindre la plaque P2 si celle-ci porte une charge négative ( des charges de signe contraire s'attirent)

en conséquence le potentiel électrique de P2 est inférieur à celui de P1 : le champ électrique est dirigé vers le plus petit potentiel.



Expression littérale de la vitesse v0 des ions qui arrivent sur la plaque P2 :

 th. de l'énergie cinétique entre P1 et P2 : (le poids est négligeable devant la force électrique)

le travail de la force électrique est : q U ; ce travail doit être moteur pour que les ions soient accélérés.

la vitesse initiale en F1 est nulle : ½ m v²0- 0 = q U d'où v²0 = 2 q U / m ; v0 =[2 q U / m]½.

La source émet maintenant, toujours avec une vitesse initiale nulle, des ions positifs de mercure 20080Hg2+ et 20280Hg2+.

Calcul de v1 et v2 pour ces deux types d'ions arrivant sur la plaque P2 :

m1 = 200 * 1,67 10-27 = 3,34 10-25 kg ; m1 = 202 * 1,67 10-27 = 3,3734 10-25 kg ; q= 2*1,6 10-19 = 3,2 10-19 C ; 2qU= 6,4 10-15.

v1 = [6,4 10-15/ 3,34 10-25 ]½=1,384 105 m/s

v2 = [6,4 10-15/ 3,3734 10-25 ]½=1,378 105 m/s

Filtre de vitesse :

Ces ions traversent ensuite la plaque P2 par la fente F2, le vecteur vitesse des ions étant ortogonal à P2. Ils pénètrent dans l'espace séparant P2 et P3 où règnent : - un champ électrique uniforme de valeur E1, parallèle à P2 et à P3, dans le plan de la feuille ; - un champ magnétique uniforme de valeur B1, perpendiculaire au plan de la feuille.
Pour parvenir au point F3 ( situé dans le prolongement de F1 et F2) la trajectoire des ions doit être rectiligne. Ces derniers sont soumis à une force électrique et à une force magnétique ; ces deux forces doivent se compenser et le mouvement est uniforme.

Si E1 = 5,3 104 V et B1 = 0,383 T, v = 5,3 104 / 0,383 =1,384 105 m/s.

Seul l''isotope du mercure 20080Hg2+ remplit ces conditions.

La valeur de B1 restant constante, on règle la valeur de E1 pour permettre le passage de l'autre ion. Au dela de F3, les ions pénèttrent dans une région où ne règne qu'un champ magnétique uniforme de valeur B2, normal au plan de la feuille.
sens de ce champ pour que les ions puissent atteindre C1 ou C2 :

Les ions ne sont soumis qu'à la force magnétique.

Cette force est perpendiculaire à la vitesse : en conséquence son travail est nul et l'énergie cinétique d'un ion ne varie pas.

La valeur de la vitesse d'un ion reste constante : le mouvement est uniforme.

La deuxième loi de Newton , ( suivant un axe perpendiculaire à la vitesse, dirigé vers le centre du cercle ) s'écrit :

2evB2 = mv²/R d'où R= mv/ ( 2eB2) = constante
La trajectoire est un arc de cercle de rayon R= mv/ ( 2eB2)

Calcul de la distance d=O1O2 =2 (R2-R1)

R1= m1v1/ ( 2eB2) = 3,34 10-25* 1,384 105 / (3,2 10-19*0,2)=0,7224 m ;

R2= m2v2/ ( 2eB2) = 3,3734 10-25* 1,378 105 / (3,2 10-19*0,2)=0,7260 m ; d=O1O2 =2 (R2-R1) = 7,2 mm.

Les quantités d'électricité reçues en une minute par les collecteurs C1 et C2 sont respectivement Q1= + 1,20 10-7 C et Q2= 3,5 10-8 C.

composition du mélange d'ions :

Les quantités d'électricité reçues en une minute par les collecteurs C1 et C2 sont proportionnelles au nombre d'ions.

20080Hg2+ : Q1/(Q1+Q2)*100 = 77,4 %.

20280Hg2+: Q2/(Q1+Q2)*100 = 22,6 %.

retour -menu