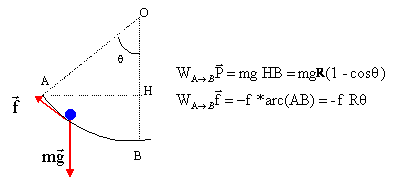|
Energie mécanique -
énergie interne
théorème de l'énergie
cinétique
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
Questionnaire à choix
multiple
Illustrer chaque choix (coché vrai ou faux) par un
exemple :
- Un système dont l'énergie mécanique est constante
- Ne peut pas être en mouvement
- Peut être soumis à une force
- Peut être soumis à des frottements
- Un système qui reçoit de l'énergie
- S'échauffe toujours
- Peut la restituer sous une autre forme¨
- Peut la garder
- La chaleur échangée
- Se mesure à l'aide d'un thermomètre
- Ne peut pas être transférée sans contact
- Peut s'exprimer en kW.h
corrigé
Un
système dont l'énergie mécanique est constante :
- Ne peut pas être en mouvement : faux ; exemple : la chute libre
- Peut être soumis à une force : vrai ; exemple : tir d'un projectile (
vitesse restant faible), chute libre
- Peut être soumis à des frottements : faux : exemple : chute réelle (
frottement fluide), l'énergie mécanique diminue
Un système
qui reçoit de l'énergie
- S'échauffe toujours: faux ; exemple : un changement d'état physique
d'un corps pur s'effectue à température constante
- Peut la restituer sous une autre forme : vrai ; machine thermique
- Peut la garder : vrai ; exemple : excitation d'un atome par un photon
( l'atome peut rester excité pendant quelques dixiemes de seconde)
La chaleur
échangée
- Se mesure à l'aide d'un thermomètre : faux ; un thermomètre repère
une température
- Ne peut pas être transférée sans contact : faux ; exemple : énergie
rayonnée par le soleil
- Peut s'exprimer en kW.h : vrai ; 1 kWh = 3600 kJ = 3,6 106
J.
|
|
|
Le saut à la
perche
Ce saut est apparu pour la première fois en Grèce
Antique. Les Crétois utilisaient cette technique pour sauter au-dessus
des taureaux. Plus tard, les Celtes ont pratiqué cette discipline pour
effectuer des sauts… en longueur. Ce n'est que vers la fin du XVIIIe
siècle, en Allemagne, que le saut à la perche se mua en concours
vertical dans le cadre de compétitions de gymnastique. A partir de
1850, les concours de saut à la perche fleurissent. L'évolution de la
discipline passera par le développement du matériel de saut. Durant
près d'un demi-siècle, à partir de 1900, la perche en bambou connaît
ses jours de gloire, puis l'acier ou le cuivre apparaissent dans les
années 50, auquel succède l'aluminium, introduit en 1957 qui porta le
record du monde à 4,73 mètres. La décennie suivante voit l'apparition
du matériau qui va révolutionner le saut à la perche : la fibre de
verre. Les principes de base du saut à la perche répondent à une
équation mathématique entre la vitesse de la course d'élan et la
flexion de la perche qui emmagasine de l'énergie restituée lors du
catapultage. La prise d'élan du sauteur doit obligatoirement dépasser
40 mètres. A l'issue d'une course d'accélération progressive, l'athlète
présente sa perche dans le butoir qui va lui permettre de faire levier.
Le franchissement de la barre fait appel à des qualités de souplesse et
de coordination du corps de l'athlète. Sergey Bubka est le premier
perchiste à franchir 6 mètres, puis 6,10 mètres. Il est l'actuel
détenteur du record du monde avec 6,14mètres.

- Sous quelle forme l'énergie du système
{perchiste-perche} se trouve-t-elle à la fin de la course, juste avant
que l'extrémité inférieure de la perche soit plantée ?
- Commentez, en vous appuyant sur le texte,
l'évolution de l'énergie interne de la perche au cours de l'ascension.
- Établir un diagramme énergétique pour le
système {perchiste-perche} au cours de l'ascension. On fera apparaître
sur ce diagramme les 3 formes d'énergie. Commenter ce diagramme
précisant l'évolution des différents types d'énergies du système au
cours de l'ascension.
- On souhaite prévoir le record d'altitude en
saut à la perche par un modèle de physique très simple : pour cela, on
pose plusieurs hypothèses simplificatrices :
- hypothèse 1 : le système est assimilé à un point matériel situé en
son centre d'inertie de masse M = 85 kg
- hypothèse 2 : la phase d'ascension s'effectue à énergie mécanique
constante
- hypothèse 3 : la vitesse du système à l'altitude maximale est nulle.
Avec ces hypothèses idéales calculer la variation d'altitude maximale
que pourrait atteindre le centre d'inertie d'un athlète à la perche
abordant la phase de saut avec une vitesse v = 10 m/s. Montrer le
record de Bubka est proche de cette limite.
- Comment pourrait-il encore améliorer la performance ?
corrigé
A
la fin de la course, l'énergie du système {perchiste-perche} se trouve
sous forme cinétique ( si on prend comme origine de l'énergie
potentielle de pesanteur, l'altitude du centre d'inertie du sauteur
lors de la course).
L'évolution de l'énergie interne ( énergie
potentielle élastique) de la perche au cours de l'ascension : "la
flexion de la perche qui emmagasine de l'énergie restituée lors du
catapultage ".
(1) perche non déformée : l'énergie interne de la
perche est nulle.
(2) perche fléchie : l'énergie interne de la
perche augmente.
(3) la perche fléchie reprend sa position non
déformée : l'énergie interne de la perche diminue et le sauteur est
catapulté.
Pour
le système {perchiste-perche} au cours de l'ascension l'énergie totale
se conserve.
dessin (1), course d'élan, l'énergie se trouve
sous forme d'énergie cinétique.
dessin (2) : l'énergie cinétique diminue ;
l'énergie potentielle de pesanteur augmente ; l'énergie potentielle
élastique de la perche augmente puis diminue lors du catapultage.
dessin (3) : l'énergie cinétique est nulle ;
l'énergie potentielle élastique de la perche non fléchie est nulle ;
l'énergie se trouve sous forme potentielle de pesanteur.
Origine
des altitudes : altitude du centre d'inertie du sauteur lors
de la course d'élan.
E= énergie initiale = énergie cinétique = ½mv0²
au cours de l'ascension, l'énergie mécanique reste
constante : E= ½mv²+mgh = ½mv0²
passage au dessus de la perche à vitesse nulle :
E= mghmax.
conservation de l'énergie mécanique : mghmax
= ½mv0² ; hmax = v0²/(2g)
= 10²/(2*9,8)= 5,10 m
soit par rapport au sol : 5,10 + altitude initiale
du centre d'inertie de l'atlète par rapport au sol ( environ 1 m)
Pour augmenter l'altitude maximale, avec les
hypothèses simplificatrices, la vitesse en fin de course doit être la
plus grande possible.
|
|
|
On se propose
d'étudier l'évolution d'un mobile (M) de masse m= 500 g au cours du
parcours proposé ci-dessous. Au départ le mobile se trouve en A. Il est
laché sans vitesse initiale. Les forces de frottement sur l'arc de
cercle AB, de rayon R=80 cm, sont considérées comme constantes,
opposées à la vitesse et représentent r=25% du poids du mobile. g =9,8 m/s² ; q=45°
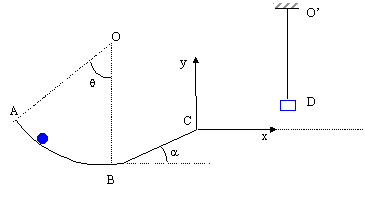
- Représenter les
forces s'exerçant sur M au cours du trajet AB.
- Calculer la
vitesse du mobile en B.
- Le mobile doit
maintenant parcourir la longueur L= 10 cm du tremplin compris entre les
points B et C, incliné d'un angle a=10°
par rapport à l'horizontale. On néglige les forces de frottement sur
cette portion BC. Quelles sont les caractéristiques du vecteur vitesse
du mobile M au point C ? Donner l'expression de la vitesse VC
en fonction de g, R, r, q, a
et L.
- Le mobile partant
de C arrive dans un petit panier repéré par le point D. Quelle doit
être la position du point D dans le repère (C, x, y) pour que le mobile
arrive en D avec le minimum d'énergie cinétique ?
- Le transfert d'énergie cinétique est supposé total. Le panier
suspendu par unfil de longueur L'= 2 m se met à osciller. On considère
que l'ensemble fil - panier - mobile constitue un pendule simple de
masse m=500 g. Les forces de frottements sont négligées. Déterminer
l'angle b d'écartement maximum du pendule simple par
rapport à la verticale en fonction de VC, a, g et L'. Calculer la période propre T0
du pendule simple.
corrigé
Vitesse du mobile en B :
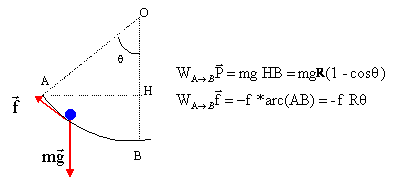
|
q
=0,785 rad ian
f = r
mg
DEc=
½ mVB², la vitesse initiale en A étant nulle
|
La variation d'énergie cinétique entre A et B est égale à la somme des
travaux des forces :
½ mVB²
= mgR(1-cosq) -f R q
= mgR(1-cosq)
-r mg R q
VB²
= 2 gR(1-cosq-r q).
VB²
= 2*9,8*0,8 ( 1-cos45-0,25*0,785) = 1,517 ; VB= 1,23 m/s.
La vitesse VC
en fonction de g, R, r, q, a
et L :
Le vecteur vitesse
étant toujours tangent à la trajectoire, est parallèle au plan incliné
et dirigé vers le haut du plan
ordonnée : VCy=
VC sin a ; abscisse : VCx= VC
cos a ;
La variation
d'énergie cinétique entre B et C est égale à la somme des travaux des
forces ;
seul le poids
travaille car l'action du plan est perpendiculaire au plan
travail résistant du
poids ( ça monte) entre B et C : -mg L sin a.
½mVC²-½mVB²=
-mg L sin a ; VC² = VB²
-2g L sin a.
remplacer VB²
par : VB² = 2 gR(1-cosq-r
q).
VC²
= 2 gR(1-cosq-r q)-2g L sin a.
Position
du point D dans le repère (C, x, y) pour que le mobile arrive en D avec
le minimum d'énergie cinétique :
l'énergie cinétique
est minimum si la vitesse est minimum : au sommet de la trajectoire
parabolique, l'ordonnée de la vitesse est nulle et l'abscisse de la
vitesse vaut VC cos a. La vitesse prend alors sa
plus petite valeur.
Energie cinétique minimum : ½mVC²
cos² a.
angle b d'écartement maximum du pendule
simple :
L'énergie cinétique finale en E est nulle pour l'angle b. DEc=
-Ec initiale en C=- ½mVC²cos²
a
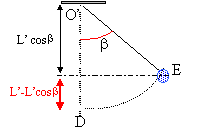
seul le poids
travaille entre D et E ; la tension du fil , perpendiculaire à la
vitesse ne travaille pas.
travail du poids
résistant ( ça monte) : -mgL'(1-cosb)
th. de l'énergie cinétique : - ½mVC²cos²
a = -mgL'(1-cosb)
; VC² cos² a
= 2gL'(1-cosb)
;
(1-cosb) = VC²
cos² a /( 2gL') ; cosb = 1-VC²cos²
a /( 2gL').
période
propre T0 du pendule simple : T0 = 2p(L'/g)½.
T0
= 2*3,14*(2/9,8)½ = 2,83 s.
|
|
Un solide S considéré
comme ponctuel de masse m= 0,690 kg se déplace sur un plan incliné
faisant un angle a=20°
avec le plan horizontal . Ce solide est relié à un axe placé sur le
bord supérieur du plan incliné et normal à celui-ci par un fil
inextensible de masse négligeable de longueur L= 0,5 m. g=9,8 m/s².
Le solide est mis en
mouvement depuis le point I avec une vitesse initiale v1.
Au cours du mouvement le fil reste constamment tendu. Le mouvement du
solide est étudié dans un repère lié à la terre et considéré comme
galiléen.
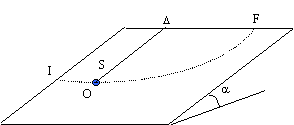
- Quel est la nature
de la trajectoire du solide ? le mouvement est-il uniforme ?
- On suppose dans
cette question que le contact entre le solide et le plan est sans
frottement. Lorsque le solide passe par sa position d'équilibre O la
vitesse v0 de son centre d'inertie a pour
vakleur v0= 2 m/s. Faire le bilan des forces
s'exerçant sur le solide et faire un schéma.
- Le solide remonte jusqu'en F, bord supérieur du plan incliné. Quelle
est en F la vitesse du mobile ?
- En raison des
frottement la vitesse en F a pour valeur vF= 0,5
m/s. Les forces de frottement sont assimilables à une force f opposée
au vecteur vitesse. La valeur de f est supposée constante, la calculer.
corrigé
La
trajectoire du solide est un arc de cercle.
Le solide est soumis
à son poids, vertical vers le bas, à l'action du plan , normale au plan
et à la tension du fil. La somme vectorielle de ces forces est
différente de zéro : d'après le principe d'inertie le mouvement n'est
pas uniforme.
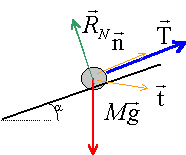
vitesse du
mobile en F :
variation d'énergie
cinétique entre O et F : DEc=
½mvF²-½mv0².
l'action du plan et
la tension du fil, perpendiculaire à la vitesse, ne travaillent pas.
travail du poids
résistant ( ça monte )de O en F : -mgL sin a.
écrire le théorème de
l'énergie cinétique : ½mvF²-½mv0²
= -mgL sin a.
vF²=
v0²-2gL sin a.
vF² = 4-2*9,8*0,5*sin20 = 0,648 ; vF=
0,805 m/s.
valeur
de f :
travail des
frottements, colinéaire à la vitesse, mais de sens contraire, de valeur
f constante, entre O et F :
valeur de f *
longueur de l'arc AB *cos180 = -f Lp/2
la différence entre
l'énergie cinétique calculée et l'énergie cinétique réelle en F est
égale au travail des frottements
-f Lp/2 = ½mv²F réelle-½mv²F
calcul.
f = m(v²F
calcul-v²F réelle)/(Lp)= 0,69(0,805²-0,5²)/(0,5*3,14)=0,175 N.
|
|
Un skieur, de masse
M= 85 kg, s'élance sur un tremplin dont la piste, de longueur 150m, est
située entre l'altitude 1638 à 1538m. Ce tremplin se termine par une
partie horizontale.
- Quelle est la
vitesse du sauteur quand il quitte le tremplin si l'ensemble des
frotements dans cette partie du saut sont équivalents à une force
constante de 350 N ?
- La piste de
réception est plane et inclinée à 45°. Elle passe par un point A situé
à la verticale de O et à 6,5 m sous lui. Déterminer la longueur du saut
(distance entre A et le point B de contact skieur piste).
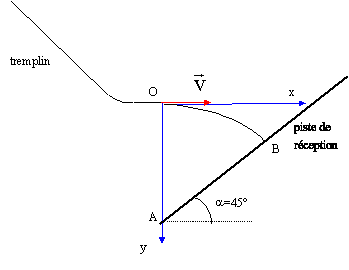
corrigé
travail
moteur du poids en descente : Mg * différence d'altitude=
85*9,8*100=83300 J
travail résistant des
frottements ( colinéaire à la vitesse, sens contraire, valeur constante
:
-f * distance
parcourue = -350*150 = -52500 J
total des travaux :
83300-52500 = 30 800 J
théorème de l'énergie
cinétique : (vitesse initiale nulle) DEc= ½Mv²-0 = ½Mv²
la variation de
l'énergie cinétique est égale à la somme des travaux des forces
½Mv² = 30800 ; v²=
2*30800/85 = 724,7 ;
v= 26,9 m/s.
suivant un
axe horizontal , le mouvement du sauteur est rectiligne uniforme x = v t
suivant un axe
vertical descendant le mouvement du sauteur est une chute libre y=½gt²
t= x/v puis repport
dans y : y = ½gx²/v² = 0,5*9,8 / 26,9² x² = 6,77 10-3
x²
équation de la droite
de réception inclinée de 45° ( pente, coefficient directeur = - tan 45
= - 1)
cette droite passe en
A, 6,5 m sous le point O d'où y = - x + 6,5
résoudre l'équation
6,77 10-3 x² = -x+6,5
6,77 10-3
x² + x-6,5 =0
D= 1²-4*6,5*6,77 10-3
= 1,176 ; x= (-1+ rac carrée (1,176))/ (2*6,77 10-3)=
6,24 m
abscisse du point B=
6,24 m ;
puis AB² = OA² + xB²
= 6,5² + 6,24²= 81,18 ; AB= 9
m .
|
|
Une voiture de masse M=800 kg, lancéeà la vitesse de
valeur v=108 km.h-1 aborde, moteur coupé, une
côte rectiligne de pente 5 % (la route s’élève de 5 m pour un parcours
de 100 m sur la route).
- A quoi est égale la pente p de la route par rapport à
l’angle a qu’elle forme
avec l’horizontale ?
- Quelle distance la voiture parcourt-elle dans la côte
avant de s’arrêter :
- si l’on néglige toutes les forces de frottement et de résistance à
l’avancement susceptibles de la ralentir.
- Si l’on suppose que toutes ces forces de frottement et de résistance
à l’avancement sont modélisables par une force (vecteur) F constante,
parallèle à la route, en sens inverse du mouvement et de valeur F=150N.
Donnée : g= 9.8N.kg-1
- La voiture est maintenant au sommet de la route
précédente mais dans le sens de la descente. Le conducteur laisse le
moteur coupé et dessere le frein à main.
- Dans les deux cas décrits à la question précédente, calculer la
valeur de la vitesse de la voiture après un parcours de 1,0 km dans
cette descente.
corrigé
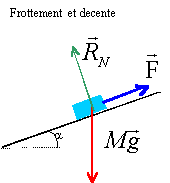
pente p =
sin a = 5/100 = 0,05
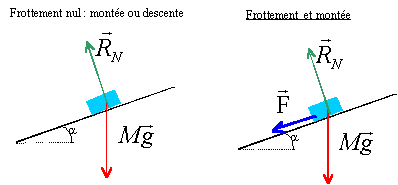
pas de
frottement : en montée le travail du poids est résistant : WP(A-->B)
= -mg AB sin a.
RN,
perpendiculaire à la vitesse ne travaille pas.
énergie cinétique
initiale : ½mv² avec v = 108/3,6 = 30 m/s
la vitesse finale
étant nulle, l'énergie cinétique finale est nulle et la variation
d'énergie cinétique vaut DEc=
0-½mv² = -½mv².
Le théorème de
l'énergie cinétique s'écrit alors : -½mv² =-mg AB sin a.
½v² = g AB sin a
soit AB = 0,5 v² / (gsin a ) = 0,5*30²/(9,8*0,05) = 918 m.
avec
frottement :
travail résistant des
frottement WF(A--> B) = -F AB
la variation
d'énergie cinétique est égale à la somme des travaux des forces : -½mv²
= -F AB -mg AB sin a.
AB = 0,5 mv² /
(F+mgsin a) = 0,5*800 *30² / (150+800*9,8*0,05)= 664 m.
pas de
frottement : en descente le travail du poids est moteur : WP(A-->B)
= + mg AB sin a.
RN,
perpendiculaire à la vitesse ne travaille pas.
énergie cinétique
initiale nulle ; énergie cinétique finale : ½mv²
la variation
d'énergie cinétique vaut DEc=
½mv²-0 = ½mv².
Le théorème de
l'énergie cinétique s'écrit alors : ½mv² = mg AB sin a.
v² = 2g AB sin a
= 2*9,8*1000*0,05 = 980 ; v = 31,3
m/s.
avec
frottement :
travail résistant des
frottement WF(A--> B) = -F AB
la variation
d'énergie cinétique est égale à la somme des travaux des forces : ½mv²
= -F AB +mg AB sin a.
v² = 2 AB( - F/m +
gsin a) = 2000*(-150/800+9,8*0,05)= 605 ; v = 24,6 m/s.
|
|
Un solide S lancé a une vitesse de valeur v0=3,0
m/s de la position A où son centre d' inertie est à la hauteur h=30 cm
au dessu du sol. Il n y a pas de frotement.
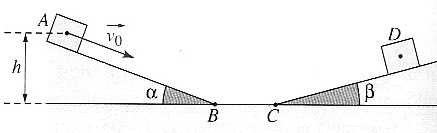
- Ecrire les expressions de l'énergie cinétique et de
l'énergie potentielle de pesanteur du solide S lorsqu'il est lancée en
A.
- Quelle transformation d'énergie s'effectue sur le
trajet AB. En déduire la valeur de la vitesse du solide S en B.
- Quel est le mouvement du solide sur BC ? Justifier.
- Quelle transformation d'énergie s'effectue sur CD ?
Quelle distance le solide parcourt-il sur CD avant de s'arrêter et de
redescendre.
masse du solide m=200 g ; a=20°
et b = 15 °
corrigé
énergie
cinétique : Ec = ½mv²
énergie potentielle
de pesanteur Ep= mgh
L'énergie mécanique
en A est sous forme d'énergie potentielle et sous forme d'énergie
cinétique ; l'énergie mécanique en B est sous forme d'énergie
cinétique.( On prend l'altitude de B comme origine des altitudes)
Sur le parcours AB
l'énergie potentielle diminue et l'énergie cinétique augmente.
L'énergie mécanique
se conserve, car seul le poids travaille : ½mvB²
= mgh +½mv0²
ou encore ½vB²
= ½v0² +gh soit vB =
racine carrée ( v0² + 2gh) avec h = 0,3 m et v0=
3m/s
vB
= (9+2*9,8*0,3)½ = 3,86 m/s.
Entre B et C le
solide est soumis à son poids et à l'action du plan, perpendiculaire au
plan. Ces forces, perpendiculaires à la vitesse ne travaillent pas et
en conséquence l'énergie cinétique ne varie pas. La valeur de la
vitesse est constante. d'après le principe d'inertie, le solide est
animé d'un mouvement rectiligne uniforme.
En C
l'énergie mécanique du solide est sous forme d'énergie cinétique : ½mvC²
= ½mvB².
En D ( arrêt)
l'énergie mécanique est sous forme d'énegie potentielle de pesanteur :
mg hC.
L'énergie cinétique
initiale se transforme en énegie potentielle.
L'énergie mécanique
se conserve car seul le poids travaille : ½mvB²=
mg hC avec hC= CD sinb.
½vB²=
gCD sinb soit CD= ½vB²/( g sinb
)
CD= 0,5*3,86² / (9,8
sin 20)= 2,22 m.
|
|
retour
-menu
|