|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||
|
|||||||||
|
|
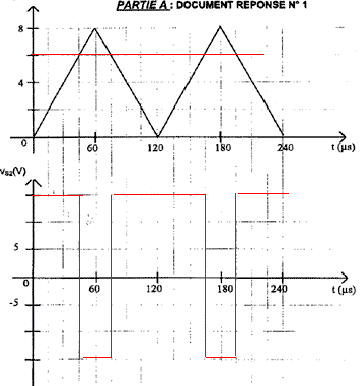
On se propose d'étudier les différents éléments entrant dans la constitution d'une trottinette électrique à balancement. Celle-ci est constituée de deux roues parallèles indépendantes et le déplacement du corps vers l'avant permet d'accélérer ou de ralentir le véhicule. L'énergie électrique nécessaire est assurée par des batteries Nickel Métal Hydrure qu'il sera nécessaire de recharger régulièrement. 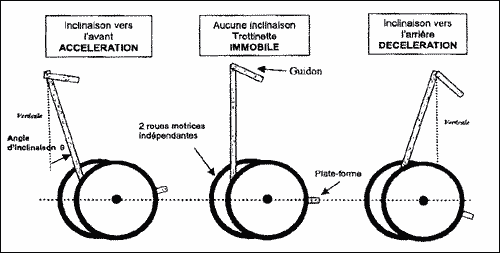 Les différentes parties du système sont les suivantes : Capteur d'inclinaison et mise en forme du signal (Fonction électronique : Partie A). Commande des moteurs des roues (Partie B). Etude d'un des deux moteurs (Moteur à courant continu : Partie C). Dispositif de recharge des batteries (Convertisseur alternatif / continu : Partie D). L'équilibre de l'ensemble, le changement de direction et la décélération sont assurés par d'autres organes, non étudiés dans le sujet. Les différentes parties du problème sont indépendantes. PartieA : capteur d'inclinaison et mise en forme du signal. Les amplificateurs opérationnels (AOP) de cette partie sont alimentés en ± Vcc. Ils sont considérés parfaits. Les tensions de saturation sont : Vsat+ = +15 V et Vsat- = -15 V. 1. Première fonction (voir figure 1) 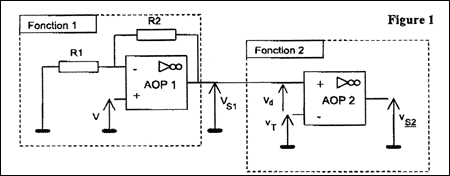 Le capteur d'inclinaison délivre une tension continue V proportionnelle à l'angle q existant entre la verticale et le tube de maintien du guidon : V = 15 10-3 q (V en volt et q en degré). Lors d'une phase d'accélération, l'angle d'inclinaison q peut prendre des valeurs comprises entre 0 et 20 degrés.
Deuxième fonction (voir figure 1) La tension VS1 est appliquée à l'entrée non inverseuse du deuxième amplificateur opérationnel (AOP2).
corrigé valeurs limites de la tension V : 0 et 15 10-3*20 = 0,3 V. V= R1i ; Vs1=(R1+R2)i avec i = V/ R1 Vs1=(R1+R2)V/ R1 = (1 + R2/R1) V VS1 = 1 V lorsque l'angle d'inclinaison a pour valeur 1 degré : alors V= 15 10-3 V Vs1/ V= 1 + R2/R1 ; Vs1/ V- 1 = R2/R1 ; R2=R1(Vs1/ V- 1) R2= 10(1/15 10-3-1)= 657 kW. fonction réalisée par l'AOP1 : amplificateur non
inverseur
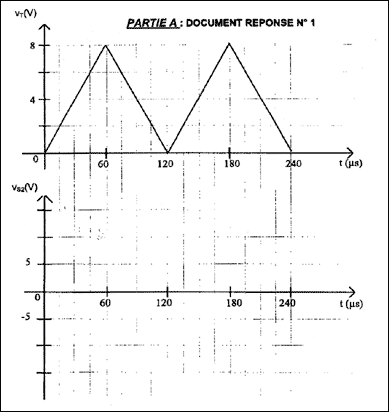
Vs2 ne peut prendre que deux valeurs + 15 V ou bien - 15 V. tension différentielle vd = Vs1 - VT. Vs2 = +15 V si Vd > 0 c'est à dire si Vs1 > VT Vs1 = 6V : si VT < 6V alors Vs2 = +15V ; si VT > 6V alors Vs2 = -15V fonction réalisée par l'AOP2 : comparateur inverseur à un seuil
|
||||||||
|
Partie B : commande des moteurs des roues (convertisseurs continu/continu) Le dispositif utilisé est représenté sur la Figure 2. II comprend : 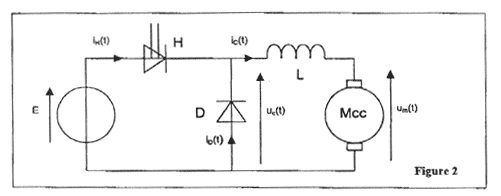 une source de tension continue de valeur E = 21V ; un interrupteur unidirectionnel commandé H supposé parfait ; une diode D supposée parfaite ; une bobine d'inductance L et de résistance négligeable. Ce dispositif alimente l'un des deux moteurs à courant continu de la trottinette. Ce moteur, à excitation indépendante, fonctionne à flux magnétique constant. L'interrupteur H est commandé à partir de la tension vS2. On considéra que sur une période T : l'interrupteur est fermé lorsque vS2 = 15V soit pour t appartenant à [ 0 ; a T ] l'interrupteur est ouvert lorsque vS2 = -15V soit pour t appartenant à [ a T ; T ] (a étant le rapport cyclique de la tension de commande)
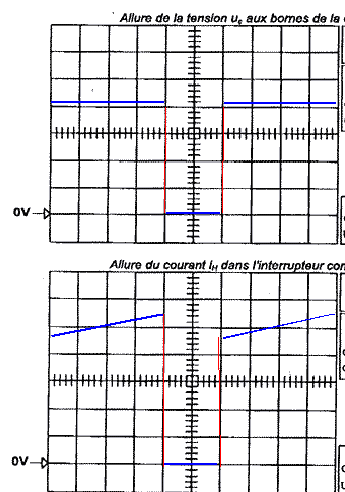
corrigé nom de ce convertisseur : hacheur série. rôle de la bobine : la bobine sert à lisser le courant ic dans la charge. valeur du rapport cyclique a =4/6 = 0,67. valeur de la fréquence f de hachage : période T : 6 divisions et 1 div correspond à 20 10-6 s. T= 6*20 10-6 = 1,2 10-4 s fréquence (Hz) = 1/T = 1/1,2 10-4 = 8,33 103 Hz. H est fermé (ic croît) : uc = E = 21 V ; ih = ic. H est ouvert (ic décroît) : uc = 0 V ( la diode devient passante) ; ih = 0.
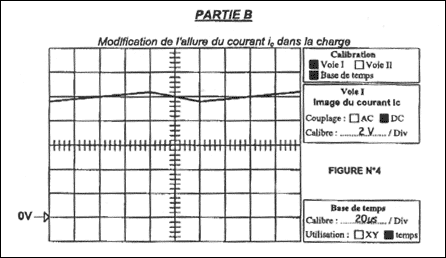
valeur moyenne < uC(t) > = aE= 4*21/6 = 14 V. valeur moyenne de la tension aux bornes de la bobine placée en série avec le moteur :< uL(t) > = 0 V valeur moyenne <um(t)> de la tension um(t) aux bornes du moteur : <um(t)>=< uL(t) > +< uC(t) > = 14 V si le rapport cyclique a augmente : <um(t)>= aE alors <um(t)> augmente et le moteur tourne plus vite. Afin de diminuer l'ondulation du courant, il est possible de modifier deux paramètres du montage sans modifier ni le rapport cyclique a , ni la tension E de la source. Sur la figure 4, la période T de ic sont identiques, donc l'iductance L de la bobine a augmenté.
|
|||||||||
|
PartieC : étude du moteur à courant continu Le moteur à courant continu est celui commandé par le dispositif de la partie B. Indications portées sur la plaque signalétique du moteur à excitation indépendante :
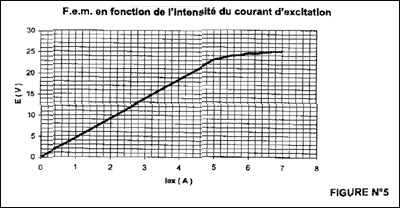
E = k F W avec k et W constantes, en conséquence E est proportionnelle au flux F. Or le flux F dépend du courant d'excitation Iex. E dépend donc de Iex. A partir d'une certaine valeur de Iex, apparaît un phénomène de saturation du champ magnétique : F , et en conséquence E sont alors constants. puissance reçue par l'induit : Pa0 = UN I0 = 21,5* 6 = 129 W. pertes par effet Joule dans l'induit : PJ0 = R I02 = 0,02*6²= 0,72 W. puissance électromagnétique : P0 = Pa0 - PJ0 = 129-0.72=128,3 W. pertes collectives Pc du moteur : P0 = Pu0 + Pc
mais à vide Pu0 = 0 W ; Pc = P0 voisin
128 W
f.e.m. E = UN - R IN = 21,5-0,02*75 =20 V. E = k F W avec avec k et F constante ( intensité d'excitation constante) : E = K W = K 2 p n = k1 n : E est proportionnelle à n. calcul de k1en charge : 20/1500 = 1,33 10-2 V min tour-1. pertes par effet Joule dans l'induit : PJR=R I2 =0,02*75² = 112,5 W. puissance utile du moteur Pu = Pa - PJS - PJR - PC avec PJS = Uex Iex=21.5*5= 107,5 W Pu =1720-112,5- 107,5- 128 = 1372 W. rendement : Pu/Pa
= 1372/1720 = 79,8%.
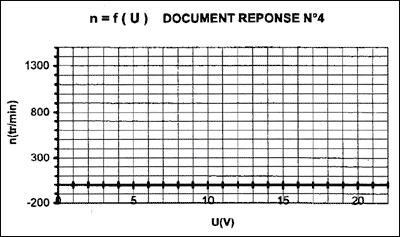
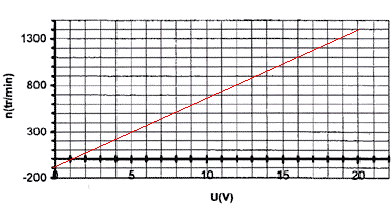
E = 13,3 10-3 n = UN - R IN n= (UN - R IN)/13,3 10-3 =( U-0,02 *75)/13,3 10-3 = 75 U - 113. tension minimale Ud qui permet de démarrer : au démarrage : n = 0 tr.min-1 soit Ud = 113/75 =1,5 V.
a mini = Ud/21 = 1,5/21 = 0,07. valeur du rapport cyclique a pour obtenir la fréquence de rotation maximale : a mini = 1 donc Umax = 21 V n = 75 U - 113 soit nmax =75*21-113= 1462 tr/min.
|
|||||||||
|
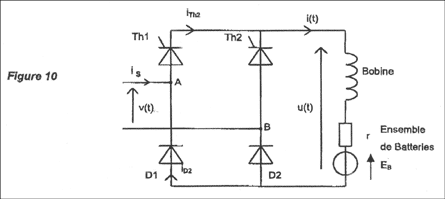
Partie D : dispositif de recharge des batteries (convertisseur alternatif/continu) On souhaite recharger les batteries de la trottinette à partir de la tension monophasée du secteur 230V/50Hz. L'ensemble des batteries admet comme modèle une source de tension EB en série avec une résistance r = 0,18W .
corrigé nom du dispositif utilisé pour abaisser la tension sinusoïdale : transformateur abaisseur de tension
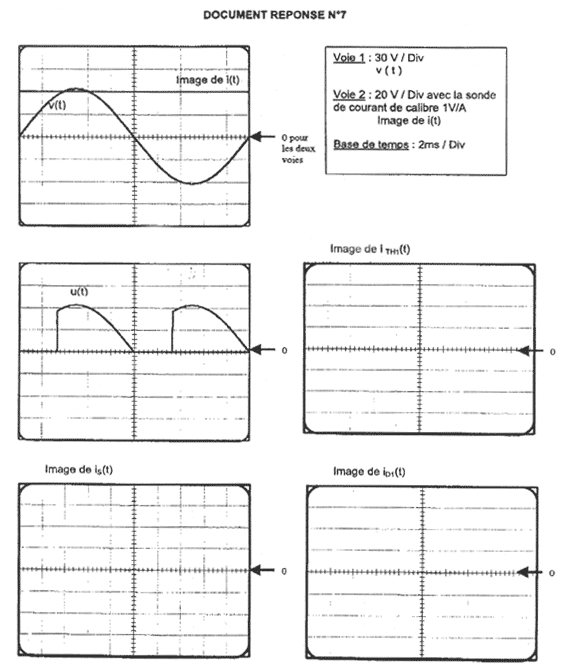
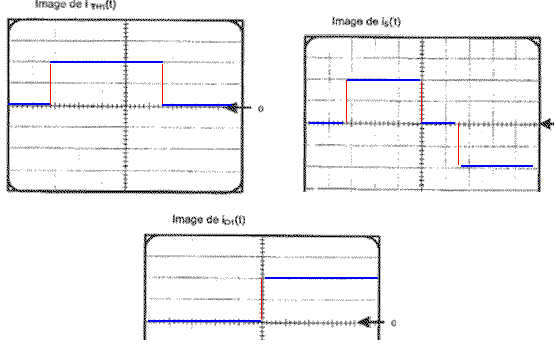
valeur t0 du retard à l'amorçage : 1,6 divisions et 2ms par division ; t0 =3,2 ms. valeur de I : 2 divisions ; 20 V/ div et sonde 1V/A soit I= 40 A.
t0 = 3,2 10-3 s et V = 2,2 div avec 30 V/div soit V= 2,2*30 = 66 V ; <u(t)>= 66/3,14(1+ cos(314*3,2 10-3)=21(1+ cos1 ) angle en radian. <u(t)>21(1+0,54)= 32,3 V. relation liant
l'intensité i(t) à la tension u(t) et les grandeurs EB, r, L. <u(t)>=0 + r<i> + EB. EB=<u(t)>- r<i> = 32,3-0,18*40 =25,1 V.
|
|||||||||
|
|