|
sonde thermique d'après bac Antilles 2005 (sans calculatrice) En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Le but du jeu est d'envoyer une bille d'acier dans un trou. Pour lancer la bille, le joueur comprime un ressort, à spires non jointives, qui va la propulser lors de la détente. La bille roule ensuite sur un plan horizontal suivant la droite AC, quitte ce plan pour chuter dans un des trous du sol. 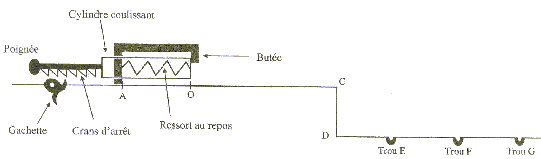 Etudions le mouvement de la bille, objet ponctuel, dans un référentiel terrestre supposé galiléen. On néglige les frottements. g= 10 m/s² ; masse de la bille m= 10 g ; constante de raideur du ressort : k= 25 N/m ; masse du ressort négligeable devant la masse de la bille. 1. Propulsion de la bille : initialement le ressort est au repos. Le joueur tire la poignée ( compression du ressort) et la bloque avec la gachette. Il place la bille contre le cylindre en A', abscisse xA'= - 10 cm sur l'axe (Ox). 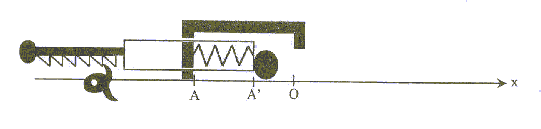
2. Chute de la bille : la bille quitte à la date t=0 le plan en C avec une vitesse vc = 5,0 m/s et de direction horizontale. 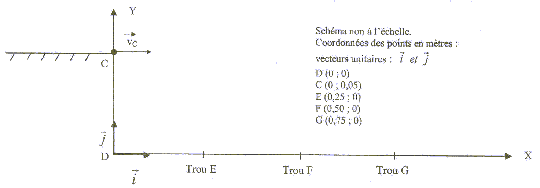
corrigé Epe(A')= ½kOA'2 avec k= 25 N/m et OA'=0,1 m Epe(A')=0,5*25*0,01= 0,12 J. Lors de la détente la bille acquiert de l'énergie cinétique Ec= ½mv² ( Ec en joule, m en kg et v en m/s) L'énergie mécanique EM du système {bille ressort} se conserve en absence de frottement. EM = ½kx²+ ½mv² avec x abscisse de A. En A' l'énergie mécanique est sous forme potentielle élastique EM= ½kOA'2 . En O l'énergie mécanique est sous forme cinétique ½mv02. conservation de l'énergie mécanique : ½mv02= ½kOA'2 = 0,12 J v02= k/m OA'2 ; v0=
(k/m )½OA'= (25/0,01)½ *0,1 = 5/0,1*0,1= 5 m/s.
chute libre : la bille n'est soumise qu'à son poids, vertical vers le bas, valeur mg La seconde loi de Newton conduit à : le vecteur accélération est identique au vecteur champ de pesanteur Dans le repère proposé : accélération( 0,-g) ; vitesse initiale ( v0; 0) position initiale (0 ; CD) la vitesse est une primitive de l'accélération : ( v0 ; -gt) la position est ne primitive de la vitesse : X(t) = v0t ; Y(t) = -½gt²+CD trajectoire : t= X/v0 ; repport dans Y : Y= -½gX²/v0² + CD Y= -0,5*10X²/25 + 0,05 = -0,2 X²+0,05. abscisse du trou où tombe la bille : Y=0 ; 0= -0,2X²+0,05 soit X²= 0,05/0,2 = 0,25 et X= 0,5 m ( trou F).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quelques valeurs numériques : log(2 10-4)= -3,7 ; 2/2,3 = 0,87 ; 2/2,7 = 0,74 ; 2/3 = 0,67 ; 1,25²= 1,56 proche 1,6 ; 4/2,5 = 1,6 ; 5/4 = 1,25 ; 100/1,25 = 80. 1. La transformation chimique étudiée : l'acide éthanoïque CH3-CO2H, ou acide acétique réagit de façon limitée avec l'eau selon: CH3-CO2H (aq) + H2O (l) = CH3-CO2- (aq) + H3O+(aq)
2. Etude pHmétrique : une solution d'acide éthanoïque, de concentration molaire initiale c1= 2,7 10-3 mol/L et de volume v1= 100 mL a un pH de 3,70 à 25°C.
3. Etude conductimétrique : on mesure ensuite, à 25°C, la conductivité d'une solution d'acide éthanoïque de concentration c2 = 1,0 10-1 mol/L. Le conductimètre indique s = 5,00 10-2 S/m.
4. Comparaison des résultats obtenus : on vient d'étudier deux solutions d'acide éthanoïque de concentrations initiales différentes.
corrigé base : espèce, ion ou molécule susceptible de gagner un proton H+. couples acide base : CH3-CO2H/ CH3-CO2- et H3O+/H2O K= [CH3-CO2-]éq [H3O+]éq/ [CH3-CO2H]éq . n1 (mol) = volume de la solution (L) * concentration (mol/L)= v1c1= 0,1*2,7 10-3 = 2,7 10-4 mol.
[H3O+] = 10-pH= 10-3,7 = 2 10-4 mol/L. xf = n(H3O+)f=[H3O+]éq v1 =2 10-4*0,1 = 2 10-5 mol. t1 =xf /xmax =2 10-5/2,7 10-4=0,2/2,7 = 2 / 2,7 *0,1 = 0,74*0,1= 2,74 10-2. t1 = est bien inférieur à 1, la transformation est limitée. [CH3-CO2-]éq= [H3O+]éq=xf /v1 =2 10-4 mol/L. [CH3-CO2H]éq =(n1-xf) //v1 = (2,7 10-4 - 2 10-5)/0,1 =2,5 10-4 / 0,1 =2,5 10-3 mol/L. K1=2 10-4 *2 10-4 /2,5
10-3 =4 10-5 / 2,5 =1,6
10-5.
La solution est électriquement neutre :[CH3-CO2-]éq= [H3O+]éq. s = l H3O+[H3O+]éq + l CH3-CO2-[CH3-CO2-]éq=(l H3O+ + l CH3-CO2-)[H3O+]éq. [H3O+]éq=s /(l H3O+ + l CH3-CO2-)= 5 10-2 / (35,9+4,1)10-3 =50/40 = 5/4 = 1,25 mol m-3 = 1,25 10-3 mol/L. [CH3-CO2-]éq= 1,25 10-3 mol/L. c2 =[CH3-CO2H]i = 0,1 ; c2/50 = 0,2/100 = 2 10-3. 1,25 10-3 < 2 10-3 donc approximation 1 vérifiée. si [CH3-CO2H]éq voisin de c2, l'acide est très peu dissocié ( sa réaction avec l'eau est très limitée) conservation de l'élément carbone :[CH3-CO2H]éq +[CH3-CO2-]éq=c2. [CH3-CO2H]éq = c2-[CH3-CO2-]éq=0,1-1,25 10-3 proche 0,1 mol/L K2=1,25 10-3 *1,25
10-3 /0,1 =1,25² 10-5 =1,56 10-5.
initialement c1<c2, mais t1> t2 : le taux d'avancement final dépend de l'état initial ; t croît si la concentration diminue affirmation 1 : vraie: t =xf /xmax et xf =[H3O+]éq. plus l'acide est dissocié, plus [H3O+]éq donc xf est grand. A xmax identique, plus xf est grand, plus t est grand. affirmation 2 : faux : en diluant ( ajout d'eau), on déplace l'équilibre CH3-CO2H (aq) + H2O (l) = CH3-CO2- (aq) + H3O+(aq) dans le sens direct, dissociation de l'acide. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
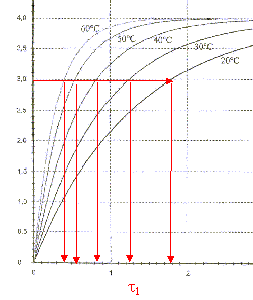
On peut constituer une sonde thermique à l'aide d'un dipôle RC série. On réalise le circuit suivant : 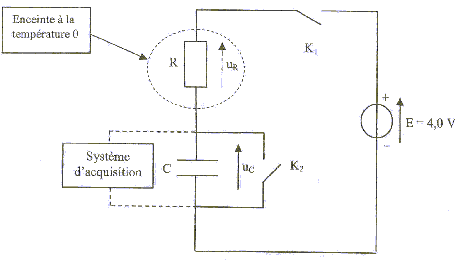 Le condensateur a une capacité C= 1 mF. Le conducteur ohmique est une thermistance : la valeur R de la résistance dépend de la température. On le place dans une enceinte dont la température interne est notée q. Un système d'acquisition permet d'enregistrer l'évolution au cours du temps de la tension uc aux bornes du condensateur. aide : 0,63*4 = 2,5 ; 0,37*4=1,5 ; 1. étalonage de la sonde : on souhaite tracer la courbe de l'évolution de la valeur de la résistance de la thermistance en fonction de la température. Le condensateur est initialement déchargé et les deux interrupteurs K1 et K2 sont ouverts. A t=0 on ferme K1 et on enregistre l'évolution de la tension uc jusqu'à la fin de la charge du condensateur. Ensuite on ouvre K1 et on ferme K2 : le condensateur se décharge complètement. On ouvre enfin K2. On modifie la température de l'enceinte et on recommence le protocole précédent. On opère pour plusieurs valeurs de température et on obtient les courbes suivantes : 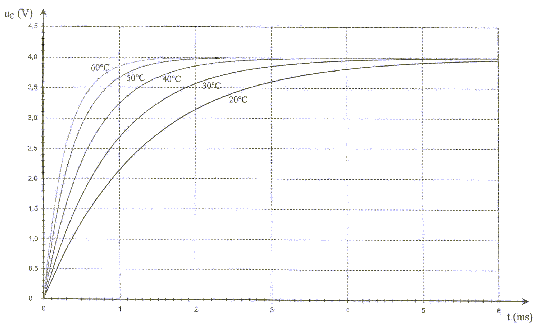
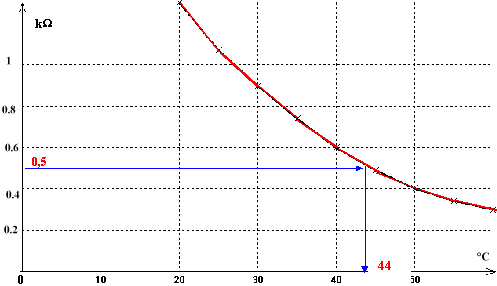
2. Mesure d'une température : Essayons la sonde thermique en la plaçant dans une enceinte de température interne q à déterminer. On mesure la résistance de la thermistance à l'aide d'un ohmmètre et l'on obtient R= 0,5 kW. A partir de la courbe d'étalonage déterminer la température de l'enceinte.
corrigé la loi d'additivité des tensions s'écrit: E = uR + uC (1) Loi d'Ohm pour un résistor : uR = Ri avec i = dq/dt et q =Cuc soit i = Cduc/dt uR = RC duc/dt repport dans l'expression (1) : E = RCduc/dt + uc équation différentielle relative à uc : duc/dt + uc /(RC)= E/(RC). uc=A+Bexp(-t/(RC)) Le condensateur est complètement chargé quand t tend vers l'infini, en conséqience uc = E. exp(-t/(RC)) tend vers zéro et on en déduit que A= E. A l'instant t = 0, le condensateur est déchargé, en conséquence uc = 0 0 = E + B = E + B d'où B = - E. uc=E(1-exp(-t/(RC))). t = RC est homogène à un temps: R résistance (ohm) = tension (volt) / intensité (ampère) soit [U][I]-1. C : capacité (farad)= charge (coulomb)/tension (volt) = intensité (A)*temps (s) / tension (V) soit [I][T][U]-1. RC : [U][A]-1 [I][T][U]-1 soit [T] E=4 V et t1 correspond à l'abscisse du point d'ordonnée 0,63*E = 0,63*4=2,5 V t1= 1,3 ms = 1,3 10-3 s.
R1= t1/C= 1,3 10-3 / 10-6 = 1,3 kW.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|