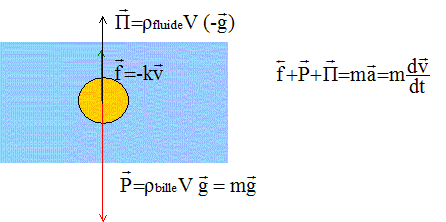|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
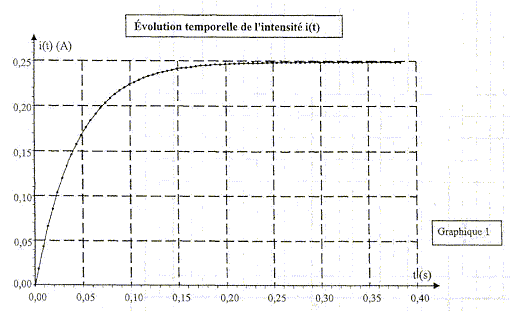
L'équation différentielle dx/dt + ax =b (1), ( a et b étant des grandeurs constantes), permet de décrire un grand nombre de phénomènes physiques variables au cours du temps: intensité, tension, vitesse, grandeur radioactive. 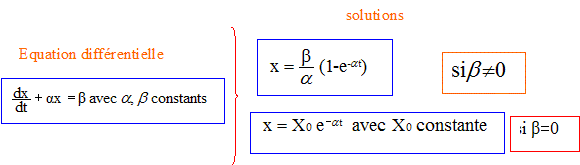 A. Dans le domaine des systèmes électriques : Cette première partie tend à montrer la validité du modèle pour un circuit électrique mettant en jeu une bobine d'inductance L et de résistance r = 11,8 ohms ,(donc non négligeable), et un conducteur ohmique de résistance R = 12 ohms, alimenté par un générateur délivrant une tension continue E = 6,1 V. 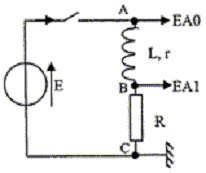 On réalise expérimentalement le circuit électrique ci-dessus. L'évolution des grandeurs variables, tension u(t) et intensité i(t), est obtenue par voie informatique. La voie EA0 permet de visualiser la tension E et la voie EAl permet de visualiser la tension UBC
partie B : dans le domaine mécanique : L'étude de la chute d'une bille d'acier, de masse m, dans un fluide de masse volumique rfluide a été exploitée grâce à un logiciel. Les capacités du logiciel permettent ensuite de faire tracer l'évolution de la vitesse du centre d'inertie en fonction du temps. Les deux courbes, expérimentale et modélisée, sont proposées ci-dessous, mais ne donnent lieu à aucune exploitation. 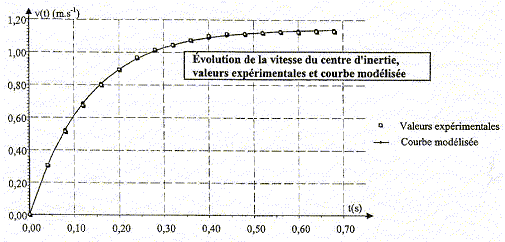
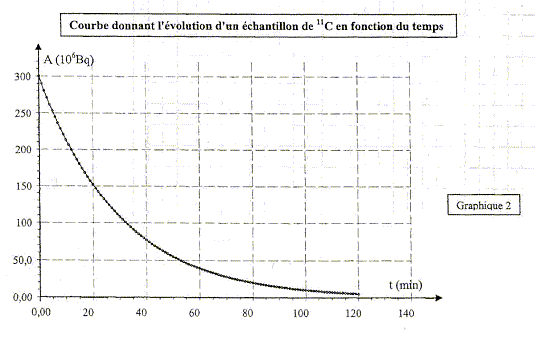
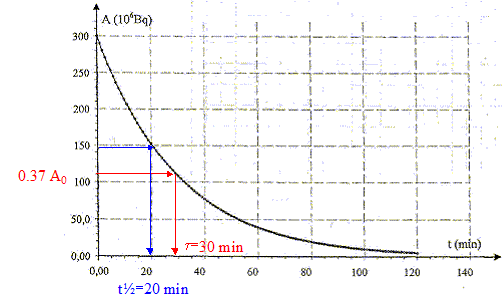
C - Dans le domaine de la radioactivité : Les traceurs radioactifs sont des radio-isotopes très utilisés en imagerie médicale pour l'exploration des organes. Des dispositifs adaptés transforment en image les mesures d'activité enregistrées. Le 11C est un traceur radioactif utilisé pour suivre en particulier l'évolution de la maladie de Parkinson. Le traceur radioactif se fixe sur le cerveau. L'activité moyenne résiduelle évolue au cours du temps selon la loi A(t) = A0exp(-lt) (4).
expression littérale de t en fonction des paramètres du circuit : t =L/(R+r)
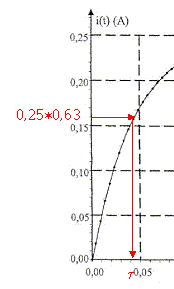
uAB = Ldi/dt + r i et uBC= Ri E= Ldi/dt + r i +Ri ; di/dt +(R+r)/L i = E/L ; on pose a= (R+r)/L et b = E/L. équation horaire littérale i(t) d'après le modèle mathématique : i(t) =b/a(1-exp(-at) i(t) = E/(R+r) (1-exp( -(R+r)t/ L) dériver par rapport au temps : di/dt = E/(R+r) exp( -(R+r)t/ L) repport dans l'équation différentielle : E/(R+r) exp( -(R+r)t/ L) + E/L(1-exp( -(R+r)t/ L) = E/L cette solution valide bien l'équation différentielle. Sachant que t = L/(R+r), cette équation horaire peut s'écrire i(t) = E/(R+r) (1-exp(-t/t)) . On appellera I l'intensité en régime permanent : au bout d'un temps suffisamment long le régime permanent est atteint et exp(-t/t) tend vers zéro; d'où I= E/(R+r) = 6,1 /(12+11,8)= 0,26 A. en accord avec la valeur expérimentale 0,25A ( écart inférieur à 4 %) Expression littérale de i(t) à la date t = t en fonction de I : à la date t = t , exp(-t/t) = exp(-1) = 0,37; 1-0,37 * 0,63 d'où i(t=t) = 0,63 I = 0,63*0,25 = 0,16A en accord avec la valeur lue sur le graphe. v(t) = 1,14(1-exp(-t/0,132)) identifié à : v(t) = b/a (1-exp(-at)) d'où a= 1/0,132 = 7,58 s-1; b/a = 1,14 soit b = 1,14 a= 1,14/0,132=8,64 m s-2. (1-exp(-t/0,132)) est sans dimension ; le second membre doit être homogène à une vitesse, en conséquence b/a est homogène à une vitesse, exprimée dans ce cas en m s-1. L'équation différentielle ayant l'équation (3) pour solution vérifie l'écriture : dv/dt + a v=b soit dv/dt + 7,58 v = 8,64 Forces appliquées à la bille : poids, vertical vers le bas, valeur mg : Vrbilleg poussée d'Archimède, verticale vers le haut, valeur P= Vrfluideg force de frottement fluide, colinéaire et de sens contraire à la vitesse, valeur f= kv, ( k=constante)
En utilisant un axe vertical orienté vers le bas, la seconde loi de Newton s'écrit : mdv/dt = -kv +mg-Vrfluide g ; mdv/dt +kv = mg-Vrfluide g ; mdv/dt +kv = g(m-Vrfluide ) dv/dt + k/m v = g(1-Vrfluide /m). expression littérale des coefficients a et b de l'équation : a = k/m et b = g(1-Vrfluide /m). valeur du coefficient b si la poussée d'Archimède était nulle : b = g Or l'équation différentielle ayant l'équation (3) pour solution vérifie l'écriture dv/dt + 7,58 v = 8,64 dans laquelle b = 8,64, valeur différente de 9,81. La poussée d'Archimède doit donc être prise en compte. analyse dimensionnelle : dans l'expression "exp(-lt) " , lt est sans dimension, en conséquence l est homogène à l'inverse d'un temps [l]=T-1. relation liant l à la constante de temps t du radio isotope : l= 1 / t. Loi d'évolution A(t) en fonction de t : A(t) = A0 exp(-t/t).
constante de temps t : à t=t, A(t)= A0 exp(-1) = 0,37 A0. demi vie t½ : durée au bout de laquelle l'activité A(t) est égale à la moitié de l'activité initiale A0. valeur de l = 1/t = 1/ 30 =3,33 10-2 min-1. A(t) = A0exp(-lt) ; dA(t)/dt = -A0lexp(-lt) ; dA(t)/dt = -lA(t) or relation liant A(t+Dt), A(t), l et Dt : A(t+Dt) = A(t) -lA(t) Dt ; A(t+Dt) = A(t)(1-lDt). La méthode d'Euler impose de se fixer un pas Dt pour effectuer les calculs. Ce pas doit être
de l'ordre du dixième de la constante de temps, c'est à dire de l'ordre
de 3 min : la valeur Dt = 15 min n'est pas
correctement adaptée à l'étude. AEuler(5)= A0(1-3,4 10-2*5)=0,83 A0= 0,83*3,00 108 = 2,49108 Bq. Athéorique(10)= A0exp(-10l)=3,00 108 exp(-3,4*0,1)=2,14 108 Bq.
Le plus grand écart est : 0,08/100 / 1,8 = 4,4% La valeur proposée pour Dt est donc correctement adaptée.
|
|||||||||||||||||||||||||||||||||
|
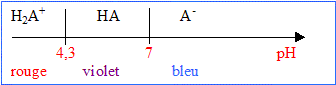
Certaines fleurs, comme celles des hortensias, possèdent des couleurs variées dues à des pigments naturels. Les couleurs rouge, mauve, violette et bleue viennent de la présence d'anthocyanines dans les pétales. La couleur violette est due à la molécule suivante que l'on notera HA dans la suite de l'exercice. 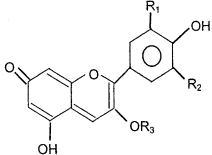
corrigé acide : espèce, ion ou molécule susceptible de céder un proton H+. couple : H2A+ / HA : forme acide : H2A+ ; forme basique HA couple HA / A- : forme acide : HA ; forme basique A- équation de la réaction de HA en tant qu'acide avec l'eau. : HA(aq)+H2O=A-(aq) +H3O+(aq) expression de la constante d'équilibre, appelée constante d'acidité, de cette réaction : K= [A-(aq)][H3O+(aq)] / [HA(aq)]= Ka2 = 10-7. rapport [A-]éq/[HA]éq =K/[H3O+(aq)] = 10-7 / 10-10 = 1000. l'espèce prédominante est A-, par rapport à HA : la
solution est bleue.
HA(aq) +H2O=H2A+(aq) +HO-(aq) expression de la constante d'équilibre K ' de cette réaction : K'= [H2A+(aq)][HO-(aq)] / [HA(aq)] Or H2A+(aq) + H2O=HA(aq) + H3O+(aq) Ka1 = [HA(aq)][H3O+(aq)] / [H2A+(aq) ] soit [H2A+(aq) ] / [HA(aq)] = [H3O+(aq)] / Ka1 repport dans K' : K'= [H3O+(aq)][HO-(aq)] / Ka1 = Ke/Ka1 domaines de prédominance des espèces H2A+ , HA et A- suivant les valeurs du pH.
Le pH de l'eau du sol absorbée par les plantes dépend du pH de ce dernier ; la sève véhicule l'eau jusqu'aux pétales. les formes acide et base ayant des teintes différentes, la couleur des fleurs est déterminée par le pH. |
||||||||||||||||||||||||||||||||||
|
|