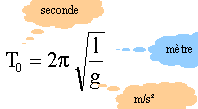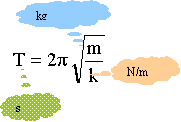|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||
| .
. |
||||||||
|
||||||||
|
|
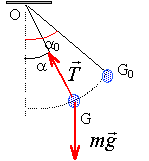
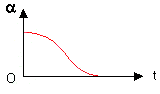
Un pendule simple est constitué d’un solide de petite dimensions, de masse m, suspendu à un point fixe O par un fil inextensible de longueur L, de masse négligeable. Ecarté de sa position d’équilibre, il oscille dans le champ de pesanteur terrestre g. Les oscillations libres : le pendule, écarté de sa position d'équilibre, est abandonné à lui même. Elles sont non amorties lorsqu'on peut négliger les frottements. référentiel : le solide Terre ; système étudié : la bille est soumise à deux forces Le poids P (action gravitationnelle de la terre sur la bille) ; la tension du fil T (action du fil sur la bille) La position d'équilibre du pendule est la position verticale. Une oscillation correspond au trajet effectué par le solide entre deux passages consécutifs par la même position, dans le même sens. L'amplitude des oscillations est la valeur maximale a0 de l'abscisse angulaire a.
travail des forces : La tension est toujours perpendiculaire à la vitesse : cette force ne travaille pas. le travail du poids est égal à : mg ( zG-zG0) l'origine des altitudes est prise au point le plus bas, la position d'équilibre.
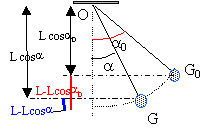
mg ( zG0 -zG) = mg ( L-Lcosa0 -L+Lcosa) mg ( zG0 -zG ) = mgL(cosa -cosa0 ). La variation de l'énergie cinétique est égal au travail des forces agissant pendant la durée de cette variation. l'énergie cinétique initiale est nulle. ½ mv²fin - 0 = mgL(cosa -cosa0 ) v²fin = 2 gL(cosa -cosa0 ) v= La' d'où : L² a '² = 2 gL(cosa -cosa0 ) diviser chaque membre par L² : a '² = 2 g /L(cosa -cosa0 ). équation différentielle : On dérive par rapport au temps l'expression précédente : 2a 'a " = 2g / L (-sina ) a ' diviser chaque membre par 2a ' : a " = g / L (-sina ) a " +g / L sina =0. approximation : si l'angle est petit, on peut assimiler le sinus de l'angle et la mesure de l'angle en radian. a " +g / L a =0. le pendule dans ce cas se comporte comme un oscillateur harmonique de période :
La période d'un pendule simple ne dépend pas de la masse dela bille accrochée à l'extrémité du fil. Cette relation doit être homogène pour les unités : seconde s, mètre m, kilogramme kg. période : [ s ] ; 2p est sans dimension longueur : [ m ] ; g : [ m ] [ s ]-2 ; l/g : [ s ]2 ; ( l/g )½ : [ s ] Si la période propre T0 est indépendante de l'amplitude angulaire a0, alors il y a isochronisme des oscillations. C'est le cas si cette amplitude angulaire a0 est inférieure à quelques degrés
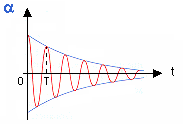
Cette diminution de l'amplitude existe déjà dans l'air mais devient très grande si le pendule oscille dans de l'eau ou mieux dans de l'huile très visqueuse.
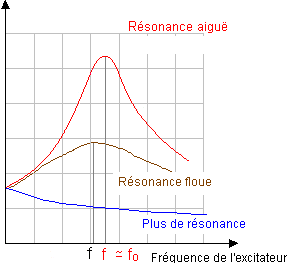
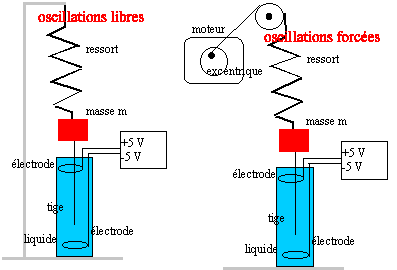
Un oscillateur, de fréquence propre f0 = 1 / T0, subit des oscillations forcées s'il oscille à une fréquence f imposée par un oscillateur extérieur appelée excitateur. L'oscillateur étudié est le résonateur. L'amplitude du résonateur passe par un maximum pour une fréquence particulière f imposée par l'excitateur (fréquence de résonance). Cette fréquence de résonance fr est proche de la fréquence propre f0 du résonateur si l'amortissement est faible. La courbe donnant les variations de l'amplitude des oscillations du résonateur en fonction de la fréquence qui lui est imposée par l'excitateur s'appelle courbe de résonance. Si l'amortissement augmente la fréquence de résonance diminue et la résonance devient plus floue. La résonance si l'amortissement devient très important.
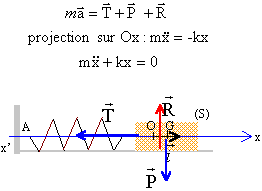
Un ressort exerce sur un solide une force de rappel T ( tension du ressort) proportionnelle à sa déformation ( allongement par exemple ) L – L0 : T = K (L – L0) K est le coefficient de raideur du ressort. On l'exprime en N / m. L : longueur du ressort déformé en mètre L0 : longueur du ressort non déformé (longueur à vide) T : force en newton. Un oscillateur élastique est constitué d'un ressort fixé à l'une de ses extrémités, l'autre de extrémité est reliée à un solide. En l'absence de frottement solide-solide, ou solide-fluide, on dit que ce pendule élastique est non amorti. Référentiel galiléen : la Terre ; système étudié : le solide de masse m. Le solide est soumis à 3 forces : P :action gravitationnelle de la Terre sur le solide (poids du solide). R action normale de la piste sur le solide.on néglige les frottements. T: tension, action du ressort sur le solide.
période T : pulsation w0 (rad/s )telle que w0²= k/m
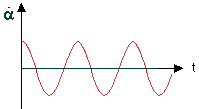
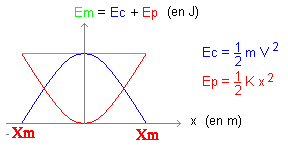
Cette relation doit être homogène pour les unités : 2 p est sans dimension: a raideur k est en newton divisée par des mètres : [N] [m]-1. une force (newton) est une masse (kg) fois une accélération (m/s²) d'où l'unité de k : [kg] [m] [s]-2 [m]-1 soit [kg] [s]-2 (masse / raideur) : [kg] [kg] -1[s]2 soit [s]2 racine carrée ( m/k) : [s] Vérifier que l'équation horaire x (t) = Xm cos ( w0 t + j) est solution de l'équation différentielle x"+ w²0x=0 dériver par rapport au temps pour avoir la vitesse x' = -Xm w0 sin (w0 t + j ) dériver la vitesse par rapport au temps pour avoir l'accélération x" = -Xm w0 ²cos (w0 t + j ) = -w0²x repport dans l'équation différentielle : -w0²x +w0²x = 0 vrai pour tout x L’énergie mécanique du système masse-ressort se conserve en l’absence de frottement. énergie mécanique = énergie potentielle élastique + énergie cinétique E=½ k x² +½ m v²
la vitesse est maximale au passage à la position d'équilibre (toute l'énergie est sous forme cinétique) la vitesse est nulle si x = Xm( amplitude) (toute l'énergie est sous forme potentielle élastique)
moteur + excentrique = excitateur ressort + masse = résonateur
résonance : l'amplitude du résonateur devient maximale. à la résonance la période de l'excitateur est proche de la période propre du résonateur. Avec une solution plus visqueuse ( frottement) la résonance sera moins aigue ( résonance floue) et peut même disparaître si l'amortissement est grand.
|
|||||||
| |
||||||||
|
|