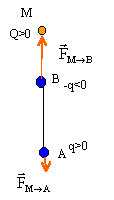Aurélie sept 04

gravitation, force de Coulomb

première S

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Un tableau donne les altitudes h( en km) et les vitesses v, en km/s de quelques satelites artificiels.

satellite
météosat
iridium
spot
ISS
vitesse v (km/s)
3,08
7,46
7,44
7,74
altitude h (km)
35800
780
830
274
rayon orbite R(km)



v*R²



R*v²



R*v



  1. Calculer d'abord le rayon R de leur orbite circulaire. On donne le rayon de la terre Rterre=6380 km
  2. Calculer les diférent produit proposés. Quel est celui est reste à peu prés constant ? En déduire la relation recherchée ?
  3. Calculer la vitesse v qu'aurait un satelite sur une orbite d'altitude h= 15000 km.
corrigé
satellite
météosat
iridium
spot
ISS
vitesse v (km/s)
3,08
7,46
7,44
7,74
altitude h (km)
35800
780
830
274
rayon orbite R(km)
42180
7160
7210
6654
v*R²
5,48 109
3,8 108
3,9 108
3,43 108
R*v²
4 105
3,98 105
3,99 105
3,99 105
R*v
1,3 105
5,3 104
5,36 104
5,15 104

R.v² qui est à peu près constante. Rv² = 4.10 5

avec h = 15000km, on a r = 15000 + 6380 = 21380 km ->

h+R=15000+6380= 21380 km

21380 . v² = 4.105

v² = 4.105 /21380 = 18,7

v = 4,32 km/s


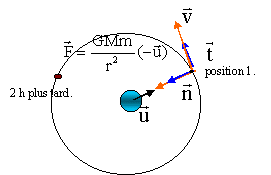
On considère un satellite de masse m en rotation autour de la terre, à une altitude h constante.

  1. Quel est le référentiel adapté a l'étude de ce mouvement ?
  2. Quelle est la trajectoire du satellite dans ce référentiel ? Quelle est la force exercée par la terre sur ce satellite? Donner son expression et calculer sa valeur. Représenter la Terre le satellite et cette force sur un shéma.
  3. Le satelitte dont la vitesse est constante, fait un tour sur son orbite en 5h47min. Calculer sa vitesse et représenter sur le shéma précédent, la position du satellite 2 h après sa position initiale. Représenter aussi la force gravitationnelle exercée par la terre sur le satellite.

Données : m= 500 kg; h=104 km; rt=6400 km; Mt=6,0.1024; G=6,67.10-11. 

corrigé
Le référentiel adapté est le référentiel géocentrique.

La trajectoire est circulaire (h=Cte)

La force de gravitation : F=G Mt m/(rt+h)²

masse en kg et distance en m.

F = 6,67.10-11 *500* 6,0.1024 /(6,4 106+107)²= 744 N.

5h47min soit t=5*60*60+47*60=20820 s

le satellite fait un tour , parcourt une circonférence : 2 p (Rt+h) =2*3,14(6,4 106+107) =1,03 108 m

vitesse : 1,03 108 /20820 = 4,9 103 m/s.

Le mouvement étant circulaire et uniforme, en 2h ( 7200 s), le satelitte parcourt :

7200/20820= 0,345 tour soit 0,345*360 = 125°.


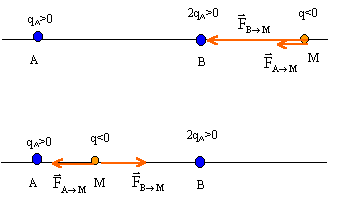
Deux corps A et B, supposés ponctuels, séparés pas une distance d, portent des charges positives qa et qb=2qa. On veut montrer qu'il existe un point M unique tel qu'un corps ponctuel portant une charge q négative placé en M subit de la part de qa et qb des forces électriques qui se compensent.

  1. Montrer que M est nécessairement situé sur la droite (AB).
  2. Montrer que M est nécessairement situé entre A et B.
  3. Exprimer la distance x=AM en fonction de d.
  4. Représenter sur un shéma les points A, B et M ainsi que les forces exercées par qa et qb sur q. 
corrigé
La charge placée en M est soumise à deux forces électriques de Coulomb

Deux forces qui se compensent sont opposées : elles ont même direction ( la droite (AB)) et sont de sens contraire.

valeur de la force de Coulomb exercées entre les charges placées en A et M : F=9 109 qA|q|/x²

valeur de la force de Coulomb exercées entre les charges placées en B et M : F=9 109 2qA|q|/(d-x)²

ces forces ont la même valeur : 9 109 qA|q|/x² = 9 109 2qA|q|/(d-x)²

1/x² = 2/(d-x)²

2x² = (d-x)²

prendre la racine carrée : 1,414 x = d-x ; 2,414 x=d

soit x= d/2,414 = 0,41 d.

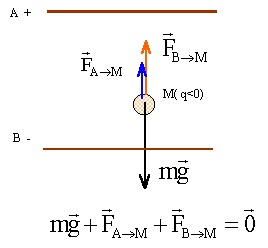
La charge élémentaire de l'électron fut déterminée expérimentalement par Robert Millikan en 1911. Lors de cette expérience, Millikan maintenait une gouttelette d'huile électrisée en équilibre entre deux plateaux horizontaux. Ces plateaux portaient des charges électriques de même valeur mais de signes opposés.

  1. Faire un shéma du dispositif utilisé par Millikan. On représentera aussi la gouttelette d'huile et les forces qui agissent sur celle-ci.
  2. Millikan répéta plusieurs fois l'expérience en faisant varier la charge de la gouttelette. Les charges qi utilisées vérifiaient la propriété suivante : q1/5=q2/8=q3/5=q4/7
    - Quelle conclusion peut-on tirer de ces mesures ?
    - Quelle est la valeur ommune de ces rapports ?
corrigé
La goutte d'huile est en équilibre sous l'action de son poids et des forces de Coulomb. A l'équilibre ces forces se neutralisent.

Les charges électriques des gouttes q1, q2, q3, q4 sont proportionnelles à la charge d'un électron -1,6 10-19 C.

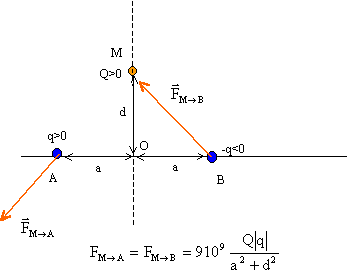
 Un dipôle est formé de deux charges ponctuelles q et -q situées en deux points A et B tels que AB=2a. Un ion positif portant la charge élémentaire positive est disposé en un point M de la médiatrice de [AB] à la distance d du milieu O de AB.

  1. Quelles sont les forces électrostatiques qui agissent sur le dipôle ?
  2. Représenter ces forces sur un shéma.
  3. Donner l'expression de la valeur de ces forces en fonction des paramètres q, a et d. Quel est l'effet de ces forces sur le dipôle ?

 

corrigé
Entre A et M, charges de même signe il y a répulsion

Entre B et M, charges de signe contraire, il y a attraction.

 

avec Q= e = 1,6 10-19 C

Sous l'action de ces forces le dipôle va tourner., présenter le point B ( charge négative) en face de M ( charge positive);

puis il y aura attraction B venant en M.

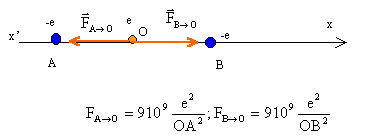
Force d'interaction entre ions :

Deux ions chlorures Cl- sont modélisés par des charges ponctuelles -e situées sur l'axe x'Ox aux points d'abscisses -a et +a avec a=0,282 nm. Un ion sodium Na+ est situé au point O. On l'assimilera à une charge ponctuelle +e.

  1. Que vaut la somme vectorielle des forces électriques subies par l'ion Na+ de la part des 2 ions Cl- ?
  2. Calculer cette somme lorsque l'ion Na+ est à l'abscisse x=0,0282 nm puis à l'abscisse x= -0,0282nm.
corrigé
La somme vectorielle des forces électriques subies par l'ion Na+ de la part des 2 ions Cl- est nulle si l'ion sodium est en O.

Les forces électriques sont opposées et ont même valeur.

si l'ion Na+ est en M, à l'abscisse x=0,0282 nm

alors AM= a+x =0,31 nm =3,1 10-10 m et MB= a-x =0,254 nm =2,54 10-10 m

Les forces sont colinéaires mais de sens contraire : la valeur de la résultante vaut :

F=FB-->O - FA-->O=9 109 e2 [1/(a-x)² - 1/(a+x)²]

F= 9 109 *(1,6 10-19)²[1/(2,54 10-10)²-1/(3,1 10-10)²]= 9*1,6*1,6 10-9[1/2,54²-1/3,1²)

F= 2,3 10-8 (0,155-0,104)=1,17 10-9 N.

si l'ion Na+ est en M, à l'abscisse x= - 0,0282 nm, la résultante a même valeur, mais elle est orientée en sens contraire de l'axe.

Trois sphères métalliques identiques S1, S2, S3 portent respectivement les charges q1=400pC, q2=250pC, q3= -650 pC.

  1. On met en contact S1 et S3. Quelles sont les charges q'1 et q'3 des sphères S1 et S3 ?
  2. On établit le contact entre S2 et S1,on les sépare puis on met en contact S2 et S3. Quelles sont les charges portées par chacune des sphères à la fin de chaque manipulation et la charge totale du système S1+S2+S3 à la fin de l'expérience?
corrigé
On met en contact S1 et S3 , la charge totale des deux sphères se conserve.

au départ : q1+q3 =400-650= -250 pC

après contact q'1+q'3 = -250 pC

les sphères étant identiques alors q'1=q'3 = -125 pC.

On met en contact S1 et S2 , la charge totale des deux sphères se conserve.

au départ : q1+q2 =400+250= 650 pC

après contact q'1+q'2 = 650 pC

les sphères étant identiques alors q'1=q'2 = 325 pC.

On met en contact S3 et S2 , la charge totale des deux sphères se conserve.

au départ : q3+q'2 = -650+325= -325 pC

après contact q''3+q''2 = -325 pC

les sphères étant identiques alors q''3=q''2 = -162,5 pC.

La charge totale du système S1+S2+S3 à la fin de chaque expérience reste constante dans la mesure où le système est électriquement isolé.


retour -menu