|
pendule élastique -radar au bord d'une route - datation au carbone 14 - le menthol - acide base En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||
| .
. |
||||||||||||||||||||||
|
||||||||||||||||||||||
|
|
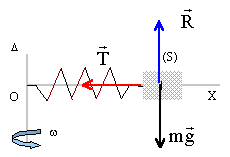
A- Un solide (S) de masse m=150 g est suspendu à un ressort élastique à spires non jointives. Ce dernier subit un allongement a0=4,9 cm. Calculer la constante de raideur k du ressort. g=9,8 m/s². B- le solide est percé selon un axe de symétrie et peut glisser sans frottement sur une tige horizontale. La tige est soudée à un axe vertical D. Le ressort précédent est enfilé sur la tige. L'une de ses extrémité est fixée à l'axe, l'autre au solide S. Lorsque le dispositif est au repos, le centre d'inertie G du solide S se trouve à une distance L= 10 cm de l'axe D. Tous les frottements sont négligés. Le niveau de référence pour l'énergie potentielle de pesanteur est le plan horizontal contenant la tige. 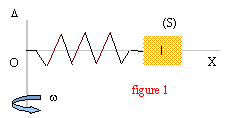
corrigé allongement et tension du ressort sont proportionnels T= ka0 avec T( N) ; a0 en mètre et k raideur en N/m. à l'équilibre la tension et le poids suspendu ont même valeur T=mg avec m en kg. d'où k= mg/ a0 = 0,15*9,8 / 0,049 = 30 N/m.
poids et action du support se neutralisent. base de Frenet : l'un des vecteur unitaire noté n est horizontal, centripète, dirigé vers l'axe de rotation l'autre vecteur est porté par la tangente à la trajectoire et a le sens de la vitesse. dans cette base l'accélération normale aN= v²/ (L+a0) = w² (L+a0) la seconde loi de Newton s'écrit suivant le vecteur unitaire n : T= mw² (L+a0) = ka0. d'où w² = ka0 / (m(L+a0)) = 30*0,049/(0,15*0,149)= 65,77 w = racine carrée (65,77) = 8,1 rad/s. l'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique énergie cinétique ½mv² = ½mw² (L+a0)² énergie potentielle de pesanteur nulle ( déplacement dans un plan horizontal) énergie potentielle élastique ( ressort déformé) : ½ka0² énergie mécanique : EM= ½mw² (L+a0)² + ½ka0² EM=
0,5*0,15*8,1²*0,149² + 0,5 *30*0,049²=0,109 + 0,036= 0,145 J.
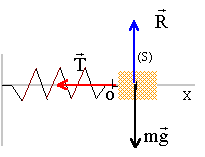
poids et action du support se compensent et T= -kx ; écrire la seconde loi de Newton suivant l'axe X mx"= -kx soit mx" + kx = 0 ou bien x" + w² x=0 avec w² = k/m x(t) = Xm cos(2pt/T0+j) à l'instant initial t=0 ; position initiale x0 = a0 ; vitesse initiale nulle. d'où a0 = Xm cos(j) ; Xm = a0 est l'amplitude positive donc cos(j) =1 et j =0 en dérivant on trouve l'expression de la vitesse : x'= Xm(-2p/T0) sin(2pt/T0+j) celle si est nulle à t=0 d'où 0 = Xm(-2p/T0)sin(j) Xmn'est pas nulle donc sin(j) = 0 et j =0 T0 est la période en seconde. T0 =2p racine carrée (m/k) = 2*3,14 rac carrée (0,15 / 30) = 0,444 s. les frottements sont négligés, en conséquence l'énergie mécanique du solide S se conserve EM= ½mv² + ½kx² à la date t=0 la vitesse est nulle et l'énergie mécanique se trouve entierement sous forme potentielle élastique ½ka0². EM= ½ka0² = 0,5*30*0,049²= 0,036 J.
|
|||||||||||||||||||||
|
On installe un radar au borsd d'une route. Ce radar est équipé d'un flash constitué notamment d'un condensateur et d'une lampe à éclat. Le condensateur de capacité C= 150 mF est chargé sous une tension continue U=330 V. Lorsque la vitesse mesurée d'un véhicule est supérieure à la vitesse limite autorisée, un système permet la décharge rapide de ce condensateur dans une lampe à éclat provoquant alors le flash. A- Etude de la puissance du flash.
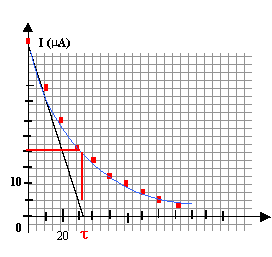
B- étude du circuit RC du flash. Après plusieurs réclamations pour déclenchement intempestif, les services techniques de la police veulent vérifier la valeur de la capacité C de ce condensateur en réalisant le montage de la figure ci-dessous. 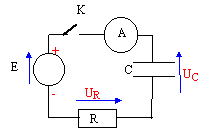 La fem E du générateur de tension continue vaut E= 12 V et sa résistance interne est négligeable. A la date t=0 on ferme le circuit et on note l'intensité du courant toutes les 10 s.
corrigé énergie stockée dans le condensateur chargé Ee= ½CU²=0,5 *150 10-6 *330²=8,16 J. puissance (W) =énergie (J) / durée (s) = 8,16 / 10-3 = 8,16 kW. à l'instant initial ( fermeture de K) la tension aux bornes du condensateur est nulle en conséquence E=RI0 soit R= E/I0 = 12/ 54 10-6 = 2,3 105 W.
l'intersection de la tangente à l'origine avec l'axe des temps donne la constante de temps t voisin de 34 s. si t = t alors l'intensité vaut 54 * e-1=54*0,368 = 20 mA la constante de temps est égale au produit : t = RC d'où C= t/ R = 34/ 2,3 105 = 1,47 10-4 F = 147 mF. écart à la valeur indiquée (150-147)/ 150 voisin de 2% : les plaintes ne sont pas justifiées.
|
||||||||||||||||||||||
|
A haute altitude un noyau d'azote 147N se transforme en carbone 146C sous l'effet du bombardement d'un neutron
146C -->AZX + 0-1e conservation du nombre de nucléons : 14 = A+0 soit A= 14 conservation de la charge : 6=Z-1 soit Z= 7 donc X est l'élément azote activité A= A0 e(-lt) avec l T½=ln2 ln (A0 /A)= lt = t / T½ ln2 soit t= T½ ln (A0 /A) / ln2 ln(1350/197 )= 1,924 t= 5590*1,924/0,693 = 15490 ans.
|
||||||||||||||||||||||
|
On considère l'alcool 5-méthyl-2-isopropylcyclohexan-1-ol, encore appelé menthol dans lequel le groupe isopropyl est -CH(CH3)2.
corrigé 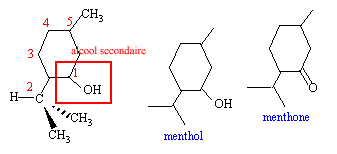
2 fois{MnO4- + 5e- + 8 H+ --> Mn2+ + 4H2O} l'alcool secondaire le menthol noté A s'oxyde en cétone la menthone notée D : 5 fois{ A--> D + 2e- + 2 H+} 2 MnO4- +16 H+ +5 A --> 2 Mn2+ + 8 H2O+ 5 D + 10 H+ masse molaire du menthol C10 H20 O : 12*10+20+16 = 156g/mol masse molaire de la menthone C10 H18 O : 12*10+18+16 = 154g/mol Qté de matière menthol : 39/156 = 0,25 mol on peut obtenir au mieux 0,25 mol de menthone masse théorique de menthone : 0,25* 154 =38,5 g rendement h= Qté réelle / qté
théorique *100 = 30,9 / 38,5*100 =80 %.
|
||||||||||||||||||||||
|
On dissout une masse m= 1 g d'un mélange de chlorure de sodium et d'hydroxyde de sodium dans de l'eau distillée de manière à obtenir une solution A de volume V = 1L. Le pH de cette solution est 12.
masse molaire NaOH : 40 g/mol ; NaCl : 58,5 g/mol. corrigé NaOH = Na+ + HO- NaCl= Na++Cl-. ions sodium, chlorure, hydroxyde et molécules d'eau sont présentes l'ion oxonium H3O+ est minoritaire ( 10-12 mol/L). [HO-] = 10-14 / 10-12 = 10-2 mol/L soit en masse 40*0,01 = 0,4 g et en conséquence 0,6 g de chlorure de sodium soit : 0,6 / 58,5 =0,0102 mol [Cl-] = 0,0102 mol/L l'ion sodium est issu de la soude et du chlorure de sodium Qté de matière d'ion sodium : 0,01 +0,0102 = 0,0202 mol dans 1 L de solution [Na+]
= 0,0202 mol/L
|
||||||||||||||||||||||
|
|