|
Contrôleur des affaires maritimes d'après concours décollage d'une fusée - meule - solénoide- tube de télevision - scooter des mers - moteur électrique - tremplin théorème de Thevenin concours 2004 - plan incliné concours 2004 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
Une fusée a une masse de 2800 tonnes. Pour la faire décoller, on fait fonctionner les 5 moteurs du premier étage, chacun d'eux créant sur la fusée une force verticale, orientée vers le haut et de valeur f = 7,0 106 N.
corrigé masse : 2.8 106 kg soit un poids de : masse *9,8 = 2,744 107 N La somme vectorielle des forces est dirigée vers le haut ( sinon on décolle pas) : poussée de moteurs - poids = 5*7 10 6-2,744 10 7 = 7,56 106 N 2ème loi de Newton : somme vectorielle des forces = masse fois accélération : accélération =
7,56 106 / 2.8 106 = 2,7 m/s².
distance = ½at² = 0,5*2,7*100 = 135 m. vitesse au carré = 2 accélération *distance parcourue en mètre v²= 2*2,7*1000 = 5400 prendre la racine carrée : 73,5 m/s.
|
|
|
Une meule entraînée par un moteur électrique tourne à la vitesse de 900 tours par minute. On coupe l'alimentation du moteur. La meule met 3 min pour s'immobiliser. Calculer :
corrigé vitesse angulaire w (rad/s) 900 / 60 = 15 tours par seconde ; w =15*2*3,14 = 94,2 rad/s. accélération angulaire a= ( w finale - w début ) / Dt=( 0-94,2)/ 180= -0,523 rad/s². l'angle décrit par la meule en 180 s est : a= ½ a t²+wt a= 0,5*(-0,523)*180² + 94,2*180 = 8478 radians 8478 / 6,28 = 1350 tours. autre méthode : w2 = 2|a| a soit a=94,22/(2*0,523)= 8478 radians
|
||
|
Une bobine assimilable à un solénoïde théorique, a une longueur l = 50 cm et comporte 200 spires régulièrement réparties. Calculer la valeur du champ magnétique à l'intérieur de ce
solénoïde lorsque l'intensité qui le traverse vaut I = 0,2 A corrigé nombre de spires par mètre n=200/0,5 = 400 champ m0 nI = 4*3,14 10-7 *400*0,2 = 10-4 tesla.
|
||
|
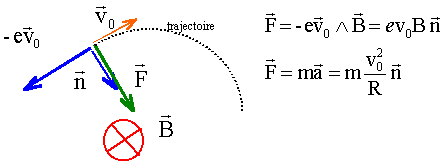
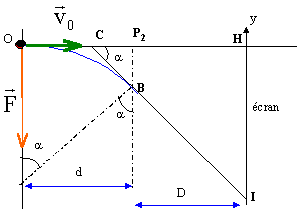
Dans un tube de télévision un faisceau d'électron pénètre en O avec une vitesse v0 horizontale dans une région où règne un champ magnétique uniforme B, horizontale, perpendiculaire à la vitesse. Le champ s'exerce entre les plans P1 et P2 ; il est nul à l'extérieur de ces plans. A l'intérieur de ces plans la trajectoire de l'électron est circulaire. Les électrons sont recueillis sur un écran. 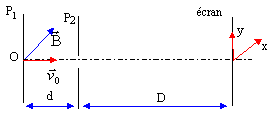
corrigé Le poids est négligeable devant la force magnétique. Entre P1 et P2 l'électron est soumis à la force magnétique F
La force F est perpendiculaire au plan défini par v0 et le champ magnétique B, donc dans le plan de la figure. La force F ne travaille pas, étant perpendiculaire à la vitesse et en conséquence ne modifie pas l'énergie cinétique de l'électron. La norme de la vitesse est constante : seule la direction de la vitesse change. le mouvement est donc uniforme entre P1 et P2 , circulaire de rayon r= mv0/(eB) r= 9,1 10-31*2,1 107 / ( 1,6 10-19 * 3,2 10-4) = 0,373 m. Au dela de P2, l'électron n'est soumis à aucune force et d'après le principe d'inertie, son mouvement est rectiligne uniforme suivant la tangente à l'arc de cercle en B.
tan a = HI / CH voisin de HI/ D de plus si a est petit ( la figure n'est pas à l'échelle) : tan a voisin de a radian. par suite : a voisin de HI/ D soit HI proche de a D Or l'arc de cercle OB est égal à ra si a est faible on peut dire que la mesure de l'arc OB est proche de d: d'où d proche de ra HI voisin de : Dd/r = 0,3*0,02/0,373 = 0,016 m = 16 mm. le mouvement s'effectue dans le plan de la figure, la déviation suivant l'axe des x est donc nulle.
|
||
|
Un scooter des mers file à une vitesse v de valeur constante 35 kmh-1 sur une trajectoire rectiligne. Il passe devant une vedette de surveillance qui démarre à l'instant où le scooter passe devant elle. La vedette suit la même trajectoire, son mouvement est rectiligne uniformément accéléré d'accélération a de valeur 0,9 m.s-2.
corrigé exprimer la vitesse en m/s :35 /3,6 = 9,72 m/s distance parcourue par le scooter ( mvt rectiligne uniforme) : d1 =9,72 * temps(s) distance parsourue par la vedette (mvt uniformément accéléré sans vitesse initiale) :d2 = 0,5 * 0,9 * temps ² =0,45 temps² au moment de la rencontre d1 = d2 soit 0,45 t² = 9,72 t d'où t = 9,72/0,45 = 21,6 s. d1 = 9,72*21,6 = 210 m. vitesse vedette : v = 0,9 * temps = 0,9*21,6 = 19,44 m/s. 19,44*3,6 = 70 km/h. 1 noeud voisin 1,83 km/h 5 noeuds voisins 1,83*5 = 9,16 km/h donc infraction du scooter.
|
||
|
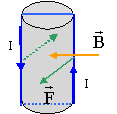
Un générateur de f.é.m. E = 220 Volts, de faible résistance interne, alimente un moteur par l'intermédiaire d'un rhéostat de résistance maximale R = 21,5 ohms. Un ampèremètre très peu résistant est inséré dans le circuit.
corrigé moteur bloqué : donc pas d'énergie mécanique, toute l'énergie électrique reçue est transformée en chaleur E= (R +r) I d'où la résistance interne du moteur : r=E/I-R= 220/10-21,5 = 0,5 ohm. le moteur tourne : E=E'+r I d'où E'= 220-0,5*10 = 215 volts. le rhéostat limite l'intensité quand le moteur est bloqué sinon celui-ci va griller. force de Laplace sur un brin : F= intensité * champ * longueur du brin ( le cadre et le champ restant perpendiculaire)
F= 10*0,5*0,1 = 0,5 N par brin.
|
||
|
On néglige les frottements et la résistance de l'air. Un mobile de masse m, assimilé à un point, est lancé sur un tremplin de longueur OA=L=1 m, faisant un angle a=30° avec l'horizontale. g = 10 m/s². La vitesse initiale v0 vaut 18 km/h. 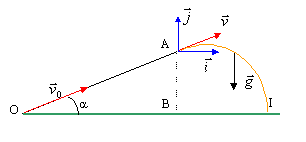
corrigé appliquer le théorème de l'énergie cinétique entre le point O et le point I. pas de frottement, l'action du plan est perpendiculaire au plan et donc ne travaille pas. l'altitude de départ est identique à l'altitude d'arrivée, donc le poids ne travaille pas. en conséquence
l'énergie cinétique du solide ne varie pas et la vitesse d'arrivée en I
est identique à v0.
à cette altitude, la composante verticale de la vitesse est nulle ; mais la composante horizontale de la vitesse n'est pas nulle. vitesse en A : appliquer le théorème de l'énergie cinétique entre O et A seul le poids travaille lors de la montée du tremplin : Wpoids = -mgLsina. ½mvA²- ½mv0²= -mgLsina. vA²= v0²-2gLsina avec v0 = 18/3,6 = 5 m/s. vA²=25-2*10*sin 30 = 15 soit vA= 3,87 m/s. lors de la chute libre au delà de A la composante horizontale de la vitesse vaut vA cos30 = 3,87 *0,866 = 3,35 m/s. vitesse horizontale au passage à l'altitude maxi de valeur v = 3,35 m/s. Ecrire que l'énergie mécanique reste constante entre le point O et l'altitude maxi: en O, énergie cinétique : ½mv0² ( O : origine de l'énergie potentielle de pesanteur) altitude maxi : ½mv²+mgH ½mv0² = ½mv²+mgH v0²
=v²+2gH soit H= (v0² -v²) / (2g) = (25-11,22) / 20 =0,69 m.
|
||
|
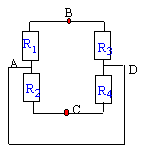
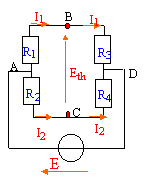
Soit le circuit ci-dessous : R1= 1 kW ; R2= 2 kW ; R3= 3 kW ; R4= 4 kW ; R5= 5 kW ; E=24 V 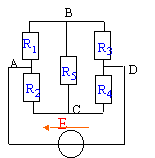
corrigé déterminer la résistance équivalente de Thévenin noté Rth.
R1 et R3 sont en dérivation entre les points B et A (ou D); elles ont équivalentes à R13 = R1 R3 /(R1+R3). R2 et R4 sont en dérivation entre les points B et A (ou D); elles ont équivalentes à R24 = R2 R4 /(R2+R4). R13 et
R24 sont en série entre les points b et C : Rth = R1
R3 /(R1+R3)+ R2 R4
/(R2+R4).
uBA+uAC=uBC=Eth ; -R1I1 + R2I2=Eth ;(1) uAC+uCD=uAD=E ;(R2 + R4)I2=E ; I2 =E/(R2+ R4) repport dans (1) uAB+uBD=uAD=E ;(R1 + R3)I1=E ; I1 =E/(R1+ R3) repport dans (1) E[-R1/(R1+ R3) + R2/(R2+ R4)]=Eth ; Eth = E [(R2 R3-R1 R4) / ((R1+ R3) (R2+ R4))] intensité dans la branche BC, dans R5 : I = Eth /(Rth+R5) I a le sens de B vers C si R3R2 >R1 R4 I est nul si R3R2 -R1 R4 =0 R3R2 =R1 R4 . |
||
|
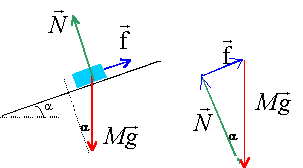
Un solide repose sur un plan incliné d'un angle a par rapport à l'horizontale. 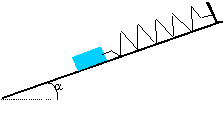
M=1 kg ; a =30° ; g=9,81 m/s² ; k=2000 N/m. corrigé 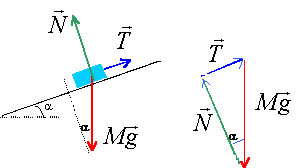
T= Mg sin a la tension et l'allongement du ressort sont proportionnels T=kx kx=Mg sin a ; x= Mg sin a /k x =1*9,81 *sin 30 / 2000 =2,45 10-3 m = 2,45 mm.
|
||
|
|
||
| |
||
|
|