Aurélie juin 04

Le grand saut (4 points)- datation au carbone 14 ( 5,5 points)

- chimie et spéléologie (6,5 points)

d'après bac Liban 2004 Calculatrice autorisée

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


Michel Fournier a le projet de franchir le mur du son en chute libre en sautant d'un ballon à una altitude de 40 000 m.

partie A : la montée en ballon.

Le ballon est constitué d'une enveloppe à laquelle est attachée une nacelle pressurisée emportant le sauteur avec son équipement. ce ballon est gonflé à l'hélium.

masse totale ( ballon + nacelle + sauteur) = m = 1600 kg ; volume total du ballon Vb=4000 m3 ; g= 9,8 m/s² ; masse volumique de l'air m= 1234 kg/m3.

Comparer la valeur du poids de l'ensemble ( ballon + nacelle + sauteur) au niveau du sol à celle de la poussée d'Archimède qui s'exerce sur le ballon et conclure.

partie B : chute libre dans la haute atmosphère

  1. Dans la haute atmosphère la température est voisine de -40°C, la pression de quelques mbar et la masse volumique de l'air de 10 g/m3. Peut-on faire l'hypothèse d'une chute libre dans cette partie du saut ?
  2. Dans cette première phase du saut, on suppose la vitesse initiale nulle au moment du largage à l'altitude de 40 km. L'accélération de la pesanteur vaut alors g=9,7 m/s². Lorsque la vitesse du son est atteinte (1067 km/h)
    - Calculer la durée de la chute depuis le largage.
    - Calculer la hauteur de chute et l'altitude atteinte.
    - Comparer ces résultats avec les valeurs réelles (altitude 35 000 m atteinte en 30 s passage du mur du son) et conclure.

partie C : chute dans la basse atmosphère

A partir de l'altitude de 10 km, le sauteur avec son équipement de masse 200 kg pénètre dans les couches denses de l'atmosphère avec une vitesse initiale de309 km/h. Dans cette zone la valeur de l'accélération de la pesanteur vaut g=9,8 m/s².

  1. On admet que l'ensemble des forces exercées par l'air sur le sauteur peut se modéliser par une force de frottement dont la valeur f est iée à la vitesse v par la relation f= kv² avec k= 0,78 unités SI. A partir d'une analyse dimensionnelle, déterminer l'unité de k.
  2. Etablir l'équation différentielle vérifiée par la vitesse v(t) au cours de la chute. On utilera un axe vertical orienté vers le bas.
  3. Pour déterminer l'évolution de la vitesse on utilise la méthode itérative d'Euler avec un pas de résolution Dt= 0,5 s.
    - Soit vn la vitesse à l'instant tn et vn+1 la vitesse à l'instant tn+1= tn+Dt. Montrer que l'équation différentielle précédente peut se mettre sous la forme vn+1 = vn + A-Bvn².
    A = 4,9 SI et B= 1,95 10-3 SI. préciser les unités des constantes A et B.
  4. En utilisant le graphe représentant la vitesse en fonction du temps, calculée avec la relation précédente, indiquer :
    - L'ordre de grandeur de la durée nécessaire pour atteindre la vitesse limite
    - La valeur de cette vitesse limite ( km/h). Comparer cette valeur à la valeur réelle de la vitesse limite( 180 km/h)

     

 

corrigé
poids au sol : mg = 1600*9,8 = 15680 N

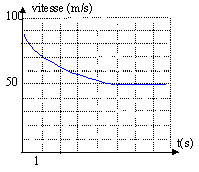
poussée d'Archimède = poids du volume d'air déplacé = Vbmg = 4000*1234*9,8 = 4,8 107 N.

la poussée est très supérieure au poids : le ballon va s'élever.

Dans la stratosphère ( 30000 - 40 000 m) il n'y a pratiquement plus d'air : en conséquence les forces de frottements sur les couches d'air sont proches de zéro .

La masse volumique de l'air à cette altitude est très faible: la poussée d'Archimède est négligeable.

Le sauteur n'est donc soumis qu'à son poids : la chute verticale est libre.

On choisit un axe vertical orienté vers le haut, l'origine étant au sol :

altitude : z= -½gt² + h0 = -4,85 t² +40000

vitesse : v = -9,7 t

éliminer le temps entre ces deux relations : z = -4,85 v²/9,7² + 40 000 avec v= 1067 / 3,6 =296,4 m/s.

z= -4,85 *296,4²/9,7²+40000 = 35 471 m

distance parcourue : 40000-35471 = 4529 m

durée de la chute : t= 296,4 / 9,7 = 30,5 s.

Valeurs en accord avec les valeurs réelles : donc l'hypothèse d'une chute libre est correcte.

k= force / vitesse ² avec force : newton = masse *accélération = masse * longueur / temps²

vitesse : longueur / temps

k : [kg][m][s]-2[m]-2[s]2 = [kg][m]-1.

Le sauteur est soumis à :

son poids vertical vers le bas, valeur mg

à la force de frottement verticale vers le haut , valeur kv²

à la poussée d'Archimède, verticale vers le haut, valeur Vmg avec V: volume d'air déplacé par le sauteur et m masse volumique de l'air.

La seconde loi de Newton s'écrit alors : ma= mg-kv²-Vmg

mdv/dt +kv² = (m-Vm)g

dv/dt +k/m v² = (1-Vm/m)g.

( vn+1 - vn ) / Dt + k/m vn² = (1-Vm/m)g.

vn+1 -vn = - kDt/m vn ²+ (1-Vm/m)gDt

vn+1 = vn - kDt/m vn ²+ (1-Vm/m)gDt

B= kDt/m et A = (1-Vm/m)gDt

A a la dimension d'une vitesse et B à la dimension de l'inverse d'une vitesse s m-1.

La vitesse limite est atteinte au bout de 5 s ( lecture graphe) après l'ouverture du parachute et sa valeur est voisine de 50 m/s soit 50*3,6 =180 km/h ( valeur en accord avec la vitesse réelle).

Etude du carbone 14.

Dans la nature le carbone 14 existe sous forme de deux noyaux isotopes 126C et 146C. Dans la haute atmosphère un neutron formé par l'action des rayons cosmiques bombarde un noyau d'azote 14 ( Z=7) qui se transforme en carbone 14 radioactif b- avec émission d'une autre particule.

  1. Ecrire l'équation de la réaction nucléaire correspondant à la formation du carbone 14. Identifier la particule émise.
  2. Ecrire l'équation de désintégration du carbone 14.
  3. Le temps de demi vie du carbone 14 est 5570 ans. Qu'appelle-t-on temps de demi vie?
  4. On appelle N0 le nombre de noyaux radioactifs dans un échantillon à un instant pris comme origine des temps.
    - Exprimer en fonction de N0 le nombre de noyaux N radioactifs restant aux dates t½, 2t½, 3t½, 4t½ et 5t½..
    - Tracer sommairement l'allure de la courbe traduisant l'évolution du nombre de noyaux radioactifs en fonction du temps.
  5. L'équation correspondant à la représentation graphique est de la forme N(t) = N0 exp(-lt)
    - Etablir l'expression entre le temps de demi vie et la constante radioactive.
    - Calculer la valeur de la constante radioactive.

Application à la datation :

Tant que la matière est vivante, les échanges de l'organisme animal ou végétal impliquant le dioxyde de carbone atmosphèrique font que le rapport N(146C) / N(126C) est constant. A la mort de l'être vivant, la fin des échanges entraîne la décroissance de ce rapport.
L'activité d'un échantillon A(t) est le nombre de désintégrations qu'il se produit par unité de temps soit A(t) = -dN(t) / dt. D'autre part cette activité est proportionnelle au nombre de noyaux radioactifs présents soit A(t) = l N(t).

  1. Etablir l'équation différentielle donnant le nombre de noyaux N(t) en fonction du temps.
    - Vérifier que l'expression de N(t) donnée N(t) = N0 exp(-lt) est solution de cette équation différentielle.
  2. Les résultats de l'analyse des ossements d'Ander et de Sapiand par la méthode du carbone 14 sont consignés dans le tableau suivant :
    nature des échantillons
    N/N0
    ossements d'Ander
    1,64 10-2
    ossements de Sapiand
    1,87 10-2
    - A partir du résultat concernant Ander calculer l'âge des ossements.
    - Sapiand a-t-il pu massacrer Ander ?
  3. Une recherche sur internet a donné l'information suivante à propos du carbone 14. 3 Pour obtenir une quinzaine de désintégrations par minute avec un matériau récent, il faut 1 g de carbone, c'est à dire 10 g de bois, de tissu ou de cuir, 20 g de coquillage ou 200 g d'os".
    - Quel est en becquerel l'activité des 200 g d'os d'un être mort récemment ?
    - Quel est le nombre de noyaux radioactifs présents dans cet échantillon ?
    - Quel est le rapport N(146C) / N(126C) dans cet échantillon ?
    masse molaire du carbone 12 : 12 g/mol ; nombre d'Avogadro : NA= 6,02 1023 mol-1.
corrigé
147N + 10n = 146C + 11H

conservation du nombre de nucléons : 14+1 = 14 +A d'où A= 1

conservation de la charge : 7+0 = 6 + Z doù Z= 1 ( élément hydrogène)

146C = 147N + 0-1e

temps de demi vie ou période : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
t½
2t½
3t½
4t½
5t½
0,5N0
0,25N0
0,125N0
0,0625N0
0,0312N0

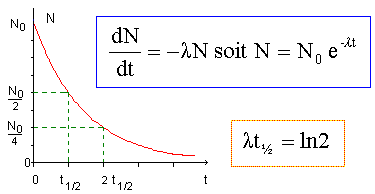
à t½ N(t) = 0,5 N0 soit : 0,5 N0 = N0 exp(-lt½)

0,5 = exp(-lt½) ; ln(0,5 ) = -lt½ ; ln 2 = lt½

l = ln2 / t½ = 0,693 / 5570 = 1,244 10-4 an-1

A(t) = -dN(t) / dt = lN(t)

dN(t) / dt + lN(t) =0

dériver par rapport au temps : N(t) = N0 exp(-lt)

dN(t) / dt = -l N0 exp(-lt)

repport dans l'équation différentielle: -l N0 exp(-lt) + l N0 exp(-lt) = 0 est bien vérifiée.

Ander : 0,0164 = exp(-lt) : ln (0,0164) = -4,11 = -lt

t = 4,11 / l = 4,11 / 1,244 10-4 = 33 038 ans.

Sapiand : 0,0187 = exp(-lt) : ln (0,0187) = -3,979 = -lt

t = 3,979 / l =3,979 / 1,244 10-4 = 31 987 ans.

1000 ans d'écart, la réponse est "non "dans la mesure ou cette méthode de datation est très précise.

activité : 15 / 60 = 0,25 Bq

A(t) = lN(t) ; N(t) = A(t) / l avec l exprimée en s-1.

l = ln2 / (5570 *365*24*3600) = 3,946 10-12 s-1.

N(t) = 0,25 / 3,946 10-12 = 6,3 1010 noyaux carbone 14.

dans 1 g de carbone il y a : 1/12*6,02 1023 = 5 1022 atomes de carbone 12.

N(146C) / N(126C) = 1,26 10-12.

Chimie et spéléologie

Données : température du laboratoire 25°C soit T= 298 K ; pression atmosphérique : Patm= 1,02 105 Pa ; R= 8,31 SI ; C: 12 ; O: 16 ; Ca : 40 g/mol ; densité d'un gaz par rapport à l'air : d=M/29 où M est la masse molaire du gaz.

Dans un ballon on réalise la réaction entre le carbonate de calcium CaCO3 et l'acide chlorhydrique (H3O+ + Cl-). Le dioxyde de carbone formé est recueilli par déplacement d'eau dans une éprouvette graduée.

Un élève verse dans le ballon un volume VS=100 mL d'acide chlorhydrique à 0,1 mol/L. A la date t=0, il introduit rapidement dans le ballon 2 g de carbonate de calcium CaCO3(s) tandis qu'un camarade déclenche le chronomètre. Les élèves relèvent les volumes de CO2 dégagé au cours du temps. La pression du gaz est égale à la pression atmosphérique.
t(s)
0
20
40
60
80
100
120
140
160
180
200
220
VCO2 mL
0
29
49
63
72
79
84
89
93
97
100
103
t(s)
240
260
280
300
320
340
360
380
400
420
440
VCO2 mL
106
109
111
113
115
117
118
119
120
120
121
La réaction chimique étudiée peut être modélisée par l'équation :

CaCO3(s) + 2H3O+ = Ca2+ + CO2(g) + 3H2O(l)

  1. Calculer la densité par rapport à l'air du dioxyde de carbone. Dans quelles parties de la grotte est-il susceptible de s'accumuler ?
  2. Déterminer les quantités de matière initiales de chacun des réactifs.
  3. Dresser le tableau d'avancement de la réaction et en déduire la valeur xmax de l'avancement maximum. Quel est le réactif limitant ?
  4. Exprimer l'avancement s de la réaction à une date t en fonction de VCO2, T, Patm et R. Calculer la valeur numérique à la date t=20 s.
    - Calculer le voilume maximum de gaz susceptible d'être recueilli dans les conditions de l'expérience. La transformation est-elle totale ?
  5. Le élèves ont calculé l'avancement x et tracé le graphe suivant :

    Donner l'expression de la vitesse volumique de réaction en fonction de l'avancement et du volume VS de la solution. Comment varie la vitesse volumique au cours du temps ? Justifier à l'aide du graphe.
    - Définir le temps de demi-réaction t½. Déterminer graphiquement sa valeur.

  6. La température de la grotte qui doit être explorée par les élèves est inférieure à 25°C.
    - Quel est l'effet de cet abaissement de température sur la vitesse volumique de réaction à la date t=0 ?
    - Tracer sur le graphe précédent l'allure de l'évolution de l'avancement en fonction du temps dans ce cas.
  7. La réaction précédente peut être suivie en mesurant la conductivité s de la solution en fonction du temps.
    - Faire l'inventaire des ions présents en solution. Quel est l'ion spectateur dont la concentration ne varie pas ?
    - On observe expérimentalement une diminution de la conductivité. Justifier sans calcul ce résultat à partir des valeurs des conductivités molaires ioniques des ions à 25°C.
    l(H3O+)=35 ; l(Ca2+)=12 ; l(Cl-)=7,5 mS m² mol-1.
    - Calculer la conductivité de la solution à la date t=0.
    - Montrer que la conductivité est reliée à l'avancement x par la relation : s =4,25-580 x.
    - Calculer la conductivité de la solution pour la valeur maximale de l'avancement.
corrigé
masse molaire CO2 : 12+2*16 = 44 g/mol

densité : d= 44/29= 1,52

Le gaz est plus dense que l'air, il est susceptible de s'accumuler dans les parties basses de la grotte.

quantité de matière d'ions oxonium : n = C.VS = 0,100*0,1= 0,01 mol

quantité de matière de carbonate de calcium ( M= 40+12+3*16) = 100g/mol): n =2/100 = 0,02 mol

CaCO3(s)
+ 2H3O+
= Ca2+
+ CO2(g)
+ 3H2O(l)
initial
0,02 mol
0,01
0
0
solvant
en cours
0,02-x
0,01 -2x
x
x
fin
0,02-xmax
0,01-2xmax
xmax
xmax
Si CaCO3 est le réactif limitant alors 2,0.10-2 - xmax =0 donc xmax = 0,02 mol

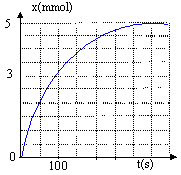
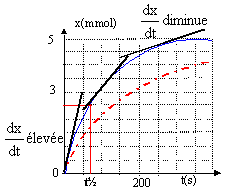
Si H3O+ est le réactif limitant alors 0,01 - 2xmax = 0 donc xmax = 5.10-3 mol

Le réactif limitant est l'ion oxonium : on retient la plus petite valeur de l'avancement maximal : xmax = 5.10-3 mol.

D'après l'équation le seul gaz dégagé est le dioxyde de carbone : on en forme "x" mol.

D'après la loi des gaz parfaits : Patm VCO2 = x R.T

x = Patm VCO2 / (RT)

à la date t = 20 s, on a VCO2 = 29 mL soit 29.10-6 m3

x = 1,02 105 * 29.10-6 / (8,31*298) = 1,2.10-3 mol

VCO2 max = xmax RT / Patm = 5 10-3 *8,31*298 / 1,02 105= 1,21.10-4 m3s= 121 mL

La transformation est totale.

v = 1/VS dx/dt

dx/dt est égal au coefficient directeur de la tangente à la courbe x(t).

Ce coefficient directeur diminue au cours du temps, en conséquence la vitesse volumique de réaction diminue au cours du temps.

Le temps de demi-réaction est la durée au bout de laquelle l'avancement x est égal à la moitié de sa valeur finale. x ( t½ = . On obtient t½ = 54 s (lecture graphique précédent)

Si la température diminue alors la vitesse volumique de réaction initiale à t= 0 s est plus petite.

La valeur de l'avancement final n'est pas modifiée ; mais il faut plus de temps (+ de 440s ) pour l'atteindre.

ions présents : H3O+, Cl- et Ca2+

L'ion Cl- est spectateur, sa concentration reste constante.

Au cours de la transformation, les ions oxonium sont consommés, [H3O+(aq)] diminue ; or leur conductivité molaire ionique est supérieure à celle des ions calcium formés. Donc s diminue.

A l'instant initial, date t = 0 s, il n'y a pas encore d'ions calcium en solution.

De plus C = [H3O+(aq)]ini = [Cl-(aq)] = 0,1*1000 = 100 mol m-3.

sini = l(H3O+) [H3O+]ini + l(Cl-)[Cl-] = (l(H3O+) + l(Cl-)) C

sini = (35+7,5) 10-3*100 = 4,25 S.m-1.

s = l(H3O+) [H3O+]+ l(Cl-)[Cl-] + l(Ca2+)[Ca2+]

s = (35 [H3O+] + 12[Ca2+] ) 10-3 +7,5*100 10-3

s =(35 (0,01-2x) + 12x ) 10-3 / VS +0,75 avec VS= 10-4 m3.

s =(0,35-70x + 12x )* 10 +0,75 = 3,5+0,75-580 x = 4,25-580 x.

smax = 4,25 - 580.xmax=4,25-580*0,005 = 1,35 Sm-1.

retour -menu