|
Indice du verre – dispersion par un prisme En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
Les longueurs
d’ondes limites, en nm, des couleurs du spectre d’une lumière blanche
sont les suivantes :
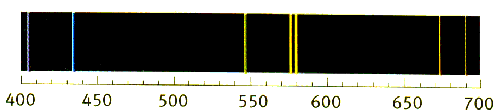
404,7 - 435,8 - 491,6 - 496 - 546,1 - 577 - 579,1 - 623,4 - 690,7
corrigé Un spectre de raies d’émission est un spectre dans lequel on distingue, sur un fond noir, un petit nombre de raies très fines, de couleurs différentes. Un gaz sous basse pression et température élevée émet un tel spectre. Dans le cas du mercure on voit 9 raies : 404,7 : violet ; 435,8 : bleu ; 491,6 - 496 - 546,1 vert ; 577 - 579,1 : jaune ; 623,4 : orange ; 690,7 : rouge montage expérimental pour observer un spectre de bandes d'absorption : mettre sur le rétropojecteur une feuille noire percée d'un fente de 1 cm de large ; placée une cuve rectangulaire, transparente, contenant la solution assez diluée de sirop de menthe. placée un réseau sur le miroir incliné du rétroprojecteur et observer le spectre sur un écran.. On éclaire le sirop de menthe avec une lampe de mercure : le sirop ne transmet que la lumière dont les longueurs d'onde sont comprises entre entre 420 nm et 560 nm On observe donc les raies fines suivantes dont les longueurs d'onde sont : 435,8 - 491,6 - 496 - 546,1
|
|||||||||||||||||||||||||||
|
L’indice d’un
milieu est fonction de la longueur d’onde de la lumière qui le
traverse. Ceci permet d’expliquer le phénomène de dispersion dans un
prisme. Le tableau ci-dessous donne l’indice de réfraction de quelques
matériaux transparents pour une radiation rouge et une radiation bleue.
corrigé vitesse de la radiation bleue dans le verre de flint : vitesse de la lumière dans le vide / indice de réfraction de la radiation bleue. v= 3 108 / 1,68= 1,79 108 m/s. Cette radiation bleue met: pour traverser 10 cm : de ce verre : temps (s) = distance (m) / vitesse (m/s) = 0,1 /1,79 108 =5,6 10-10 s. dans l'air : 0,1 /3 108 =3,33 10-10 s. Cette différence de temps est bien trop petite pour mesurer l’indice de réfraction de ce verre.
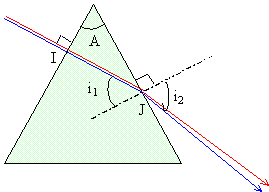
en I, le rayon incident est perpendiculaire à la surface séparant l'air du verre : donc pas de déviation. en J, l'angle d'incidence i1 vaut : i1 = A = 30.( i1 et A ont le même complément (JA, JI)). calcul de i2 à partir de la loi de Descartes : nverre sin i1 = nair sin i2 avec nair = 1 ; sin i1 = sin 30 = 0,5 pour le bleu : 1,68 * 0,5 = sin i2 bleu. sin i2 bleu = 0,84 ; i2 bleu = sin-1(0,84)= 57,1°. pour le rouge : 1,596 * 0,5 = sin i2 rouge. sin i2 rouge = 0,798 ; i2 rouge = sin-1(0,798)= 52,9°. Le prisme, comme les gouttes d'eau, disperse la lumière blanche: on observe un arc en ciel dans lequel le bleu est le plus dévié.
|
||||||||||||||||||||||||||||
|
Les limites des longueurs d'ondes (en nm) des couleurs du
spectre d'une lumière blanche sont les suivantes :
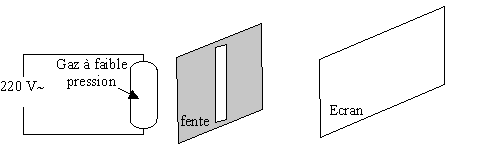
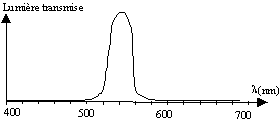
corrigé Disposer un réseau entre la fente et l'écran pour observer le spectre du gaz enfermé dans l'ampoule. Longueurs d'ondes des différentes raies du spectre : 405 nm : violet ; 435 nm : bleu ; 548 nm : vert ; 575 et 580 nm : jaune ; 670 et 690 nm : rouge Le gaz est de la vapeur de mercure. Intervalle des longueurs d'ondes des radiations que laisse passer ce filtre : [525 nm ; 575 nm ] Ce filtre transmet le vert ; la couleur du filtre, éclairé en lumière blanche, est verte : il absorbe le magenta, mélange du rouge et du bleu, couleur complémentaire du vert. On interpose le filtre précédent entre l'écran et la fente du montage représenté ci-dessus : seules les radiations dont les longueurs d'onde sont comprises entre [525 nm ; 575 nm ] sont transmises , les autres sont absorbées.
Il s'agit d'un spectre de raies |
||||||||||||||||||||||||||||
|
En étudiant théoriquement l'origine thermique de l'émission de lumière, le physicien allemand Wilhelm Wien a établi une loi importante qui porte son nom. Elle relie la température T d'un corps chaud, exprimée en kelvin (K), à la longueur d'onde lmaxi pour laquelle le rayonnement est le plus intense : lmaxiT= A A est une constante qui est la même pour tous les corps, quelle que soit leur nature : A = 2,9 10-3 dans le système internationale d'unités.
corrigé lmaxi est une longueur exprimée en mètre. lmaxiT= 2,9 10-3 soit lmaxi = 2,9 10-3 /T= 2,9 10-3 /2973 = 9,7 10-7 m = 970 nm. Le domaine du spectre est l'infra rouge. lmaxiT= 2,9 10-3 soit T= 2,9 10-3 / lmaxi = 2,9 10-3 / 4,6 10-7 =6300 K. A cette température le fer ou le tungstène ne seront plus à l'état solide. T= 2,9 10-3 / lmaxi = 2,9 10-3 / 7,8 10-7 = 3718 K. T= 2,9 10-3 / lmaxi = 2,9 10-3 / 4 10-7 = 7250 K. Un corps dont la température T est comprise entre 3718 K et 7250 K émet des radiations dont les longueurs d'onde maximales lmaxi appartiennent au domaine visible. |
||||||||||||||||||||||||||||
|
|