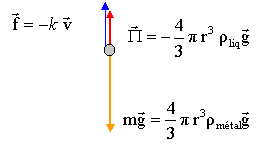Aurélie sept 04

chute d'une bille, oscillations mécaniques, projectile

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


chute d'une bille

 

Une bille de masse m = 100 g est en chute verticale dans un fluide visqueux. On donne les variations de la vitesse au cours du temps.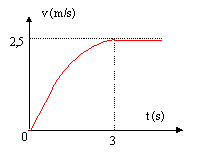

  1. Quelle est la trajectoire de la bille ?
    - Nommer les deux régimes du mouvement.
    - Evaluer le temps caractéristique du mouvement.
  2. Nommer et représenter les forces s'exerçant sur la bille lors de la chute.
    - Quelle relation vérifient ces forces dans la seconde partie de la chute ?
    - L'une des deux équations suivantes modélise le mouvement de la bille :
    dv/dt = - 4 v + 10 (1) ; dv/dt = - 4 v2 + 10 (2)
    - Laquelle des deux est-elle en accord avec la courbe? Justifier.

 

 

corrigé
La a bille est animé d'un mouvement rectiligne.

sur l'intervalle [0 ; 3 s], la vitesse augmente : mouvement accéléré

au delà de 3s, la valeur de lavitesse est constante : mouvement uniforme.

Le temps caractéristique du mouvement est obtenu en traçant la tangente à l'origine au graphe proposé ; l'intersection de la tangente et de l'asymptote horizontale donne t voisin de 1,8 s.

La bille est soumise à son poids, à la pousée d'Archimède et à une force de frottement fluide dont la valeur peut être proportionnelle à la vitesse ( ou au carré de la vitesse).

D'après le principe d'inertie ( 1ère loi de Newton), lorsque la vitesse limite est atteinte, la bille est pseudo-isolée ( la somme des vecteurs forces appliquées à la bille est nulle)

Lorsque la vitesse limite est atteinte dvlim/dt=0

dv/dt = - 4 v + 10 donne : - 4 vlim + 10 soit vlim=2,5 m/s (accord avec le graphe)

dv/dt = - 4 v2 + 10 donne : - 4 v2lim + 10 soit vlim=(2,5 )½= 1,6 m/s (désaccord avec le graphe)

oscillations mécaniques

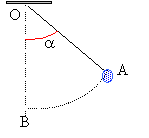
Un dispositif est constitué d'une bille de masse m suspendue à un fil de longueur L.

 

  1. A quelle condition ce dispositif peut-il être assimilé à un pendule simple ?
  2. On donne le graphe montrant l'évolution de l'angle a en fonction du temps.( à t=0, a = 10°)

    - Quelle est la nature des oscillations ?
    - Déterminer la période des oscillations.

  3. Lors d'une nouvelle acquisition, on a obtenu le graphe ci-dessous ; quel est le paramètre du dispositif expérimental qui a été modifié et dans quel sens ?
  4. On a réalisé un enregistrement dans les mêmes conditions que l'acquisition n°1, mais sur une durée plus longue. Commenter le graphe ci-dessous.
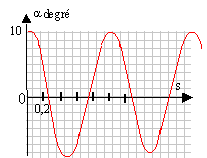
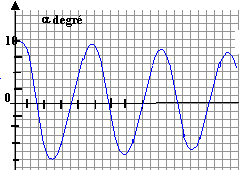
corrigé
pendule simple : la bille doit être assimilable à un objet de très petite dimension ( ponctuel)

Les oscillations sont périodiques sinusoïdales.

La période vaut T= 0,5 s d'après le graphe.

La période du pendule a doublé : T' = 1 s.

L'expression de la période d'un pendule simple est T= 2p (L/g)½ ;

La période étant proportionnelle à la racine carrée de la longueur L du pendule , si la période double, alors L quadruple.

Le dernier graphe présente une diminution lente de l'amplitude des oscillations ; cela est dû aux forces de frottements qui dissipent de l'énergie. Le mouvement est amorti.


projectile

 

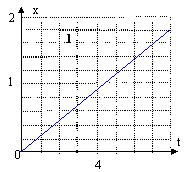
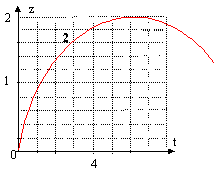
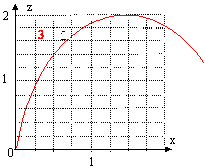
On étudie le mouvement d'une balle dans un champ de pesanteur uniforme en filmant le mouvement de cette balle avec un caméscope fixé au sol enregistrant 25 images par seconde. Le film est observé image par image sur l'écran d'un téléviseur à l'aide d'un magnétoscope. On relève les coordonnées du centre d'inertie de la balle dans un repère (O ; i, k) défini par un axe (Ox) horizontal et un axe (Oz) vertical ascendant. La date t = 0 est choisie sur la première image.

  1. Quel référentiel faut-il choisir pour l'étude ? Justifier.
    - Héliocentrique ; - Géocentrique ; -Terrestre
  2. On propose quatre graphes :
    - Quel est le graphe représentant la trajectoire de la balle ? Justifier
    - Quel est la nature du mouvement projeté sur Ox. Justifier.
    - En déduire la valeur de la vitesse vx selon l'axe Ox.
  3. On propose 3 modèles mathématique de la composante vz de la vitesse selon l'axe Oz.
    (1) vz = -9t ; (2) vz= -9t + 6 ; (3) vz= -15 t2 + 6
    Justifier votre choix en donnant un sens physique à chacune des constantes du modèle retenu.

 

corrigé
Héliocentrique : adapté dans le cas de l'étude des planètes du système solaire.

Géocentrique : adapté dans le cas de l'étude des satellites de la terre.

Le référentiel terrestre est adapté pour étudier le mouvement de la balle.

le graphe 3 représente la trajectoire car il donne la hauteur z en fonction de l'abscisse x. La fonction correspondante est de la forme z = -a x² + bx. Dans cette expression le temps n'y figure pas.

La seule force agissant sur la balle est le poids, de direction verticale : en conséquence cette force ne modifie pas la composante horizontale de la vitesse initiale et le mouvement de la balle projeté sur Ox est un mouvement uniforme.

De plus l'abscisse x est une primitive de la composante horizontale de la vitesse : le graphe représentant la fonction x=f(t) sera une droite croissante avec le temps ( graphe 1). Le coefficient directeur de cette droite donne vx.

vx voisin de : 0,9 / 4 = 0,22 m/s.

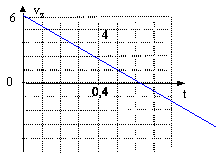
composante vz de la vitesse selon l'axe Oz.

D'après le graphe (4) la courbe est une droite de coefficient directeur négatif ;

ce coefficient est proche de -6/0,6 soit environ 10

Le modèle suivant est à retenir : vz= -9t + 6

La dérivée de vz par rapport au temps donne la composante verticale de l'accélération ( -9 m s-2).

La constante +6 donne la valeur de la composante verticale de la vitesse initiale en m/s.


retour -menu