La télé-loupe, bts Opticien lunetier 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... La télé-loupe est composée d’un objectif achromatique de distance focale image f 'Ob = 24,0 mm, d’un système prismatique redresseur de grandissement transversal gyr = −1 et d’un oculaire de distance focale image f 'oc = 9,00 mm. Les éléments baignent dans l’air. L’objectif est modélisé par une lentille mince de centre O, de foyers objet Fob et image F 'ob. Le redresseur (afocal) est représenté par le couple de plans conjugués anti-principaux (gyr= −1) intervenant dans ce système. L’oculaire est représenté par ses points principaux objet Hoc et image H 'oc, ainsi que par ses foyers objet Foc et image F 'oc. FONCTION DU SYSTÈME OPTIQUE (6 points) On considère que le plan objet réel [A] se situe à 330 mm de l’objectif . Le technicien utilisateur de la télé-loupe est emmétrope et n’accommode pas. La chaîne des conjugués (sur l’axe optique) du système s’écrit : 1. Déterminer la mesure agébrique OA′, par le calcul, puis montrer que le grandissement transversal gyobj correspondant est égal à −7,8 × 10-2 environ. 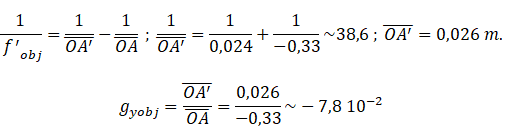2. Préciser la position de A′′′. En déduire la position de A′′ en fonction de celles des points représentant l’oculaire. Le technicien étant emmétrope et n’accommodant pas, A''' est à l'infini. A" doit être au foyer objet FOC de l'oculaire. Le système télé-loupe est représenté sans souci d’échelle. Les objet et image conjugués 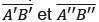 sont placés sur les plans anti-principaux du redresseur (soit gyr=-1). 3. Compléter la construction en déterminant graphiquement la position de AB, conjugué objet de A'B'   par l’objectif, ainsi que la position de l’image de A'"B'"à travers l’oculaire. 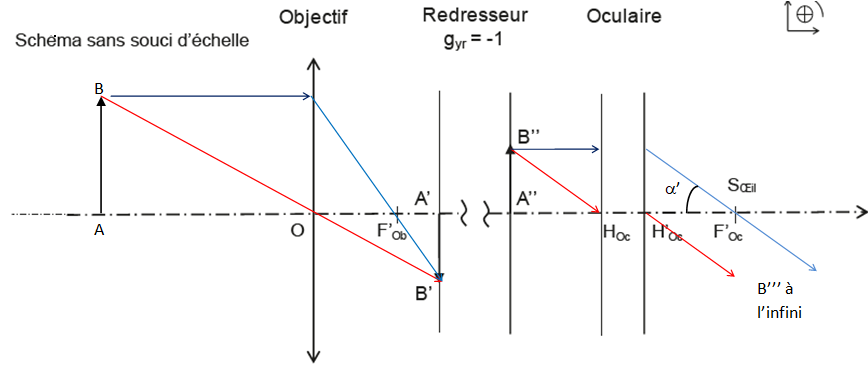On rappelle que la définition du grossissement G d’un système s’écrit G =|tan a' / tan a | . L’oeil du technicien est repéré par le point Soeil. Les angles a et a′ sont respectivement l’angle sous lequel est vu l’objet à l’oeil nu et l’angle sous lequel est vue l’image par la télé-loupe. 4. Représenter a' sur le document  et faire un autre schéma sur la copie (sans souci d’échelle), pour représenter a. a est l'angle sous lequel l'observateur voit l'objet à oeil nu. 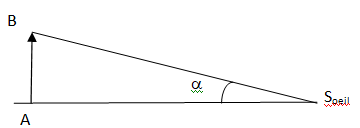tan a = AB / ASoeil.  ASoeil= AB / tan a. 5. Montrer que G = |gyr x gyob xSoeilA / fOc| où foc est la distance focale objet de l’oculaire et SoeilA la distance OEil-Objet. 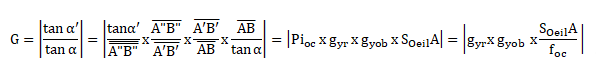6. Calculer G. Indiquer si la valeur obtenue est conforme aux caractéristiques techniques de la télé-loupe. G = --1 x(-7,84 10-2 x 400 / 9| ~3,5. Cette valeur est conforme aux caractéristiques techniques. PARTIE 2 - Étude du champ du système (5 points) On se propose d’étudier, à présent, le champ de la télé-loupe. La monture de l’objectif correspond au diaphragme d’ouverture. Son diamètre est 2Rob = 13 mm. Entre le redresseur et le doublet oculaire se trouve un diaphragme Doc de diamètre 2Roc = 11 mm. On considère que le redresseur ne limite pas le champ de l’instrument. Pour réaliser l’étude de champ, on se place dans l’espace optique intermédiaire à l’objectif et au redresseur. Dans cet espace interviennent la monture de l’objectif ainsi que le conjugué intermédiaire de Doc, appelé D. Sa position par rapport à l’objectif est : mesure algébrique OD = 8,5 mm. Comme le redresseur afocal est caractérisé par un grandissement transversal égal à – 1, la dimension transversale de D est 2R = 11 mm. On considérera que le plan des champs intermédiaire à l’objectif et au redresseur se situe à 26 mm de l’objectif. 1. Représenter le rayon du champ de pleine lumière intermédiaire rpli. 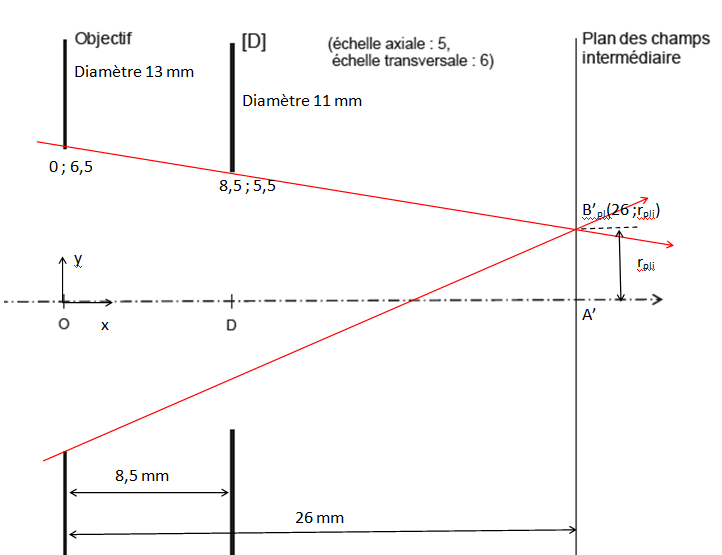2. Déterminer, par le calcul, le rayon rpli. Equation de la droite y = ax +b. Pour le bord supérieur de l'objectif : 6,5 = 0 x a+b ; b= 6,5. Pour le bord supérieur de D : 5,5 = 8,5 a +6,5 soit a = (5,5-6,5) / 8,5 ~ -0,118. Au point  B'pl : rpli = -0,118 x23 +6,5 ; rpli =3,44 mm. Dans le plan des champs intermédiaire, il y a un diaphragme de diamètre 6,8 mm. 3. Préciser le rôle de ce diaphragme et justifier le choix de sa dimension. Le diaphragme élimine le champ de contour. Son diamètre est un peu inférieur au diamètre du champ de pleine lumière soit :  2 rpli = 6,88 mm. 4. Montrer que le champ de pleine lumière objet (largeur du champ visuel), noté 2rpl, est à peu près conforme aux caractéristiques techniques de la télé-loupe. 2rpl = 2 rpli / |gyob| =6,88 / (7,84 10-2)~86 mm, valeur conforme). La puissance de la télé-loupe est P = 8,75 d 5. Calculer le champ de pleine lumière image (angle). P = tan a' / AB ; tan a' = AB x P avec AB exprimé en mètre. tan a'pl = rpl x P=43 10-3 x8,75 =0,376 ; a'pl =20,5°. PARTIE 3 – Limite de résolution (2,5 points) La fabrication horlogère est délicate à cause des dimensions minuscules des roues et des pignons et de la précision nécessaire des engrenages. La distance entre deux dents consécutives est de 7 à 8 centièmes de millimètre. L’utilisateur de la télé-loupe doit s’assurer qu’il lui sera possible de distinguer les fins détails des pièces horlogères. 1. Calculer la limite angulaire elim de résolution imposée par la diffraction. On rappelle que elim =1,22 l / (2R0) où 2R0 est la diamètre de la pupille d’entrée du système et l la longueur d’onde du rayonnement. Pour le calcul, on prendra la longueur d’onde l = 555 nm et 2R0 = 13 mm. elim =1,22 x 555 10-9 / (13 10-3) =5,21 10-5 rad 2. En déduire que la dimension transversale ylim du plus petit détail discernable dans le plan objet est tel que ylim = 17 µm. 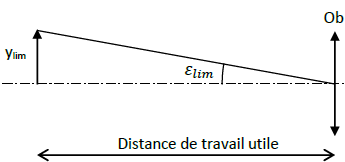ylim = distance de travail utile x tan elim ~distance de travail utile x  elim =0,330 x5,21 10-5 =1,72 10-5 m ~17 µm On considère que la limite de résolution de l’oeil est eoeil = 3,0 × 10-4 rad. La puissance de la téléloupe est P = 8,75 d. 3. Montrer que la dimension yoeil du plus petit détail observable dans le plan objet est yoeil =34 µm. P = tan a' / AB. yoeil = tan eoeil /P ~eoeil /P = 3 10-4 /8,75 =3,4 10-5 m = 34 µm. 4. Préciser, en justifiant, si c’est la diffraction ou l’oeil qui limite la résolution de l’ensemble (téléloupe + oeil). yoeil > ylim : l'oeil limite la résolution. 5. Préciser, en justifiant, si l’horloger peut distinguer deux dents consécutives du mécanisme horloger. Distance entre 2 dents consécutives : 0,08 mm soit 80 µm > yoeil. L'horloger peut distinguer deux dents consécutives. ... .... PARTIE 4 – ÉTtude de l'éclairage (3 points) Le technicien utilise la télé-loupe avec un éclairage dédié. Caractéristiques de cet éclairage Source : DEL (diode électroluminescente) puissante, mobile et légère Alimentation : batterie lithium-polymère (3 700 mAh, 3,7 V) Compatible avec le produit KS Température de couleur : 5 500 K Éclairement : 20 000 lx à une distance de 250 mm Temps d’utilisation pleine puissance : 4 h Temps de charge : environ 4 h La norme relative à l’éclairage des lieux de travail impose notamment un éclairement moyen Emoy à maintenir. Pour des tâches nécessitant la perception de détails, il est préconisé un éclairement moyen de la zone de travail supérieur à 750 lx. 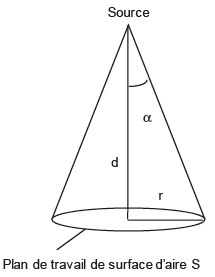Pour simplifier, on considère que la source éclaire le plan de travail sous incidence normale. Dans ce cas, la loi de Bouguer liant l’intensité lumineuse I (en candelas) à l’éclairement E (en lux) s’écrit E = I / d2  où d est la distance (en mètres) entre la source et le plan éclairé . 1. Calculer l’intensité lumineuse I de la source. I = Ed2 =20 000 x 0,252= 1250  cd. 2. Montrer qu’à la distance de travail utile (0,33 m), l’éclairement Eu est égal à 11 480 lx environ. Commenter. Eu = I / d2 =1250 / 0,332 =1,15 104 lx > 750 lx. On peut bien distinguer les détails. Le faisceau émis par la source est conique de demi-angle d’ouverture a = 20° . 3. Montrer que l’aire S de la surface éclairée circulaire de rayon r est S = 4,5 × 10-2 m2 environ pour la distance de travail utile. tan a =tan 20 ~0,364 = r / d. r = 0,364 d = 0,364 x0,33 =0,12 m. S = p r2 =3,14 x0,122 =4,5 10-2 m2. 4. Calculer F sachant que l’éclairement Eu est le flux lumineux F (en lumens) émis par la source et reçu par unité de surface de travail utile. Eu = F /S ; F =EuS =11480 x 0,045=520 lm. Le développement des éclairages à DEL blanche s’est largement accentué depuis quelques années, notamment à cause de rendements lumineux élevés. 5. En considérant que le rendement h de la source est égal à 100 lm ∙ W-1, calculer la puissance électrique P consommée (on rappelle que le rendement est le rapport du flux lumineux émis et de la puissance électrique consommée). Rendement = F / P : P = F / rendement = 520 / 100 = 5,2 W. 6. Commenter le résultat précédent sachant que pour un même flux, une lampe à filament de tungstène consomme 35 W. 5,2 << 35 : l'éclairage LED consomme moins d'électricité. pour la même efficacité d'éclairage. PARTIE 5 – Optimisation de la transmission du système (3,5 points) L’objectif de la télé-loupe est un doublet achromatique ; l’oculaire est composé de trois lentilles et il y a quatre transmissions dans l’ensemble redresseur. Pour simplifier, on considère que tous les composants optiques de la télé-loupe sont taillés dans un même matériau et on néglige toute absorption dans le domaine spectral considéré. 1. Justifier que l’instrument est composé de N = 14 dioptres. L'objectif étant un doublet, il est composé de 2 lentilles soit 4 dioptres. L'oculaire étant composé de trois lentilles, soit 6 dioptres. Le système redresseur compte 4 transmissions soit 4 dioptres. Total : N =4 +6 +4 = 14. On précise que le coefficient de transmission en intensité d’un dioptre est Tdioptre = 0,958. 2. Calculer la transmission de la télé-loupe Ttéléloupe dans ce cas sachant que la transmission d’un système à N dioptres est égale à TNdioptre. 0,95814 =0,548 ou 54,8 %. Cette transmission n’est pas suffisamment élevée pour ce type d’instrument. Le constructeur traite tous les dioptres soumis à transmission avec un traitement antireflet. 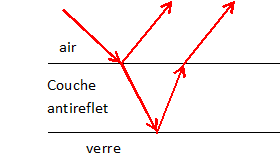3. Expliquer le principe physique du traitement antireflet monocouche. L’explication devra être illustrée d’un schéma clair.  Ce traitement a pour but de former des interférences destructives entre le rayon réfléchi par la face supérieure de la couche antireflet et le rayon réfléchi par le dioptre couche anti-reflet-verre.  Il faut obtenir 2 vibrations de même intensité lumineuses en opposition de phase. En fait, c’est un traitement multicouches qui est réalisé. La figure suivante présente les courbes de coefficient de réflexion en intensité R d’un dioptre en fonction de la longueur d’onde. 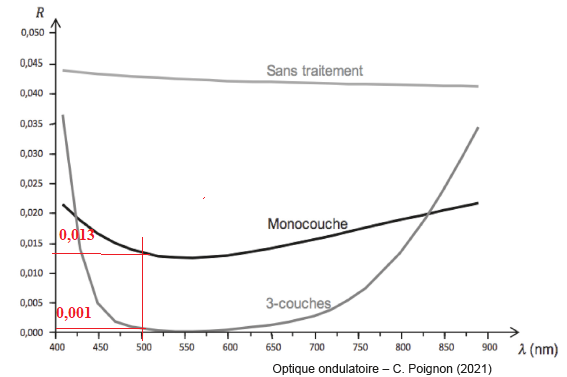4. Justifier, en s’appuyant sur la figure  l’utilisation du traitement multicouches (3-couches) en termes de transmission. Le traitement 3 couches possède un coefficient de réflexion  inférieur au traitement monocouche dans tout le spectre visible. Le traitement multicouches réduit la quantité de lumière réfléchie et augmente le coefficient de transmission. On considère, dans le domaine spectral, la longueur d’onde l = 500 nm. 5. Calculer la transmission de la télé-loupe dans le cas d’un traitement monocouche, puis dans le cas d’un traitement multicouche. Commenter. T = 1-R. Traitement monocouche : T téléloupe = (1-0,001)14=0,986 ou 98,6 %. Traitement multicouche : T téléloupe = (1-0,013)14=0,833 ou 83,3 %. Le traitement multicouche est plus efficace que le traitement monocouche. ane.

menu