Mathématiques,
bac Métropole 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 .5 points.
La directrice d’une école souhaite réaliser une étude auprès des étudiants qui ont passé l’examen
de fin d’étude, pour analyser la façon dont ils pensent avoir réussi cet examen.
Pour cette étude, on demande aux étudiants à l’issue de l’examen de répondre individuellement à
la question : « Pensez-vous avoir réussi l’examen ? ». Seules les réponses « oui » ou « non »
sont possibles, et on observe que 91,7 % des étudiants interrogés ont répondu « oui ».
Suite à la publication des résultats à l’examen, on découvre que :
- 65 % des étudiants ayant échoué ont répondu « non » ;
- 98 % des étudiants ayant réussi ont répondu « oui ».
On interroge au hasard un étudiant qui a passé l’examen.
On note R l’événement « l’étudiant a réussi l’examen » et Q l’événement « l’étudiant a répondu
« oui » à la question ».
.
Dans tout l’exercice, les probabilités sont, si besoin, arrondies à 10-3 près.
1. Préciser les valeurs des probabilités P(Q) et Pnon R(non Q).
P(Q) =0,917.
Probabilité que le candidat interrogé ait répondu "non" sachant qu'il a échoué : Pnon R(non Q) =0,65.
2. On note x la probabilité que l’étudiant interrogé ait réussi
l’examen.
a. Recopier et compléter l’arbre pondéré ci-dessous.
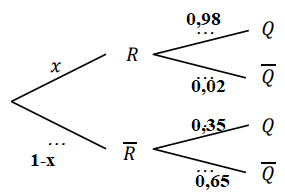
b. Montrer que 𝑥 = 0,9.
0,917 = 0,98 x +0,35(1-x) ; 0,917 = 0,98x -0,35x +0,35.
0,917-0,35 =0,63 x ; x = 0,567 / 0,63 =0,9.
3. L’étudiant interrogé a répondu « oui » à la question.
Quelle est la probabilité qu’il ait réussi l’examen ?
PQ(R) = P(Q n R) / P(Q) =0,9 x0,98 / 0,917 =0,962.
4. La note obtenue par un étudiant interrogé au hasard est un nombre entier entre 0 et 20. On
suppose qu’elle est modélisée par une variable aléatoire N qui suit la loi binomiale de
paramètres (20 ; 0,615). La directrice souhaite attribuer une récompense aux étudiants ayant
obtenu les meilleurs résultats.
À partir de quelle note doit-elle attribuer les récompenses pour que 65 % des étudiants soient
récompensés ?
P(N > 11) ~0,797 ; P(N > 12) ~0,649.
A partir de 12, la directrice récompense 65 % d'entre eux.
5. On interroge au hasard dix étudiants.
Les variables aléatoires N1, N2, … , N10 modélisent la note sur 20 obtenue à l’examen par
chacun d’entre eux. On admet que ces variables sont indépendantes et suivent la même loi binomiale de paramètres (20 ; 0,615).
Soit S la variable définie par S = N1+ N2+ … + N10
Calculer l’espérance E(S) et la variance V(S) de la variable aléatoire S.
E(Ni) =20 x0,615=12,3.
V(Ni) = 20 x0,615 x(1-0,615)=4,7355.
E(S) = E(N1) +...+E(N10) =12,3 +... +12,3 = 123.
Les variables aléatoires étant indépendantes : V(S) = V(N1) +...+V(N10) =10 x4,7355 =47,355.
6. On considère la variable aléatoire M = S /
10
.
a. Que modélise cette variable aléatoire M dans le contexte de l’exercice ?
M représente la moyenne des notes obtenues par un échantillon de 10 étudiants choisis au hasard.
b. Justifier que E(M) = 12,3 et V(M) = 0,47355.
E(M) = E(S) / 10 =126 / 10 = 12,3.
V(M) =V(S) / 102 = 0,47355.
c. À l’aide de l’inégalité de Bienaymé-Tchebychev, justifier l’affirmation ci-dessous.
« La probabilité que la moyenne des notes de dix étudiants pris au hasard soit strictement
comprise entre 10,3 et 14,3 est d’au moins 80 % ».
L'intervalle [10,3 ; 14,3] est centré sur l'espérance de M. On cherche la probabilité de l'événement A = { M-E(M) < 2}.
L'évnement contraire est non A = {|M-E(M)| > 2}.
P{|M-E(M)| > 2} < V(M) / 22 ; P{|M-E(M)| > 2} < 0,47355 / 4.
P{|M-E(M)| > 2} < 0,1183875.
P{|M-E(M)| < 2} > 1-0,1183875.
P{|M-E(M)| < 2} > 0,8816.
L'affirmation est correcte.
Exercice 2. 5 points.
Les parties A et B sont indépendantes.
Alain possède une piscine qui contient 50 m3
d’eau.
Pour désinfecter l’eau, il doit ajouter du chlore.
Le taux de chlore dans l’eau, exprimé en mg. L−1 , est défini comme la masse de chlore par unité
de volume d’eau. Les piscinistes préconisent un taux de chlore compris entre 1 et 3 mg. L−1
.
Sous l’action du milieu ambiant, notamment des ultraviolets, le chlore se décompose et disparaît
peu à peu.
Alain réalise certains jours, à heure fixe, des mesures avec un appareil qui permet une précision à
0,01 mg. L−1
. Le mercredi 19 juin, il mesure un taux de chlore de 0,70 mg. L−1
.
Partie A : étude d’un modèle discret.
Pour maintenir le taux de chlore dans sa piscine, Alain décide, à partir du jeudi 20 juin, d’ajouter
chaque jour une quantité de 15 g de chlore. On admet que ce chlore se mélange uniformément
dans l’eau de la piscine.
1. Justifier que cet ajout de chlore fait augmenter le taux de 0,3 mg. L−1
.
15 / (50 103)=3 10-4 g / L=0,3 mg / L.
2. Pour tout entier naturel 𝑛, on note vn le taux de chlore, en mg. L−1, obtenu avec ce nouveau
protocole n jours après le mercredi 19 juin. Ainsi v0 = 0,7.
On admet que pour tout entier naturel n, vn+1 = 0,92vn + 0,3.
a. Montrer par récurrence que pour tout entier naturel n, vn ≤ vn+1 ≤ 4.
v1 =0,92 x 0,7 +0,3 =0,944.
Initialisation : la propriété est vraie au rang zéro.
Hérédité : vn ≤ vn+1 ≤ 4.est supposé vrai.
0,92 vn ≤ 0,92 vn+1 ≤ 0,92 x4 =3,68.
0,92 vn +0,3 ≤ 0,92 vn+1 +0,3 ≤ 3,68+0,3=3,98.
. vn+1 ≤ vn+2 ≤ 4. La propriété est vraie aurang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
b. Montrer que la suite (vn) est convergente et calculer sa limite.
La suite est croissante et bornée par 4, donc elle converge.
A la limite : l = 0,92 l+0,3 ; 0,08 l = 0,3 ; l = 3,75.
3. À long terme, le taux de chlore sera-t-il conforme à la préconisation des piscinistes ? Justifier
la réponse.
3,75 n'appartient pas à l'intervalle [1 ; 3]. Le taaux de chlore ne sera pas conforme.
4. Reproduire et compléter l’algorithme écrit en
langage Python pour que la fonction alerte_chlore
renvoie, lorsqu’il existe, le plus petit entier n tel que vn > s.
def alerte_chlore(s)
n=0
u=0.7
while u <=s
n=n+1
u =0.92*u+0.3
return n
5. Quelle valeur obtient-on en saisissant l’instruction
alerte_chlore(3) ? Interpréter ce résultat dans le contexte
de l’exercice.
v16 =2,96 ; v17 =3,01 > 3. Le programme renvoie 17.
17 jours après le 19 juin, le taux de chlore sera trop élevé.
Partie B : étude d’un modèle continu.
Alain décide de faire appel à un bureau d’études spécialisées. Celui-ci utilise un modèle continu
pour décrire le taux de chlore dans la piscine.
Dans ce modèle, pour une durée x (en jours écoulés à compter du mercredi 19 juin), f(x)
représente le taux de chlore, en mg. L−1, dans la piscine.
On admet que la fonction f est solution de l’équation différentielle (E) ∶ y′ = −0,08y + q/
50, où q est
la quantité de chlore, en gramme, rajoutée dans la piscine chaque jour.
1. Justifier que la fonction f est de la forme f(x) = Cexp(−0,08x) + q/
4
où C est une constante réelle.
Solution générale de y'+0,08y = 0 : y = C exp(-0,08x) avec C une constante réelle.
Solution particulière de (E) : y =q /(50 x0,08) =q / 4.
Solution générale de (E) : f(x) = C exp(-0,08x) + q /4.
2.
a. Exprimer en fonction de q la limite de f en +∞.
En +oo le terme en exponentielle tend vers zéro et f(x) tend vers q / 4.
b. On rappelle que le taux de chlore observé le mercredi 19 juin est égal à 0,7 mg. L−1
.
On souhaite que le taux de chlore se stabilise à long terme autour de 2 mg. L−1. Déterminer
les valeurs de C et q afin que ces deux conditions soient respectées.
2 = q / 4 soit q = 8.
A t =0 : 0,7 = C+q / 4 = C +2 ; C = -1,3.
|
...
|
....
|
Exercie 3. 6 points).
On considère une fonction f définie et deux fois dérivable sur ]−2 ; +∞[. On note Cf sa courbe
représentative dans un repère orthogonal du plan, f ′ sa dérivée et f ′′ sa dérivée seconde.
On a tracé ci-dessous la courbe Cf et sa tangente T au point B d’abscisse −1.
On précise que la droite T passe par le point A(0 ; −1).
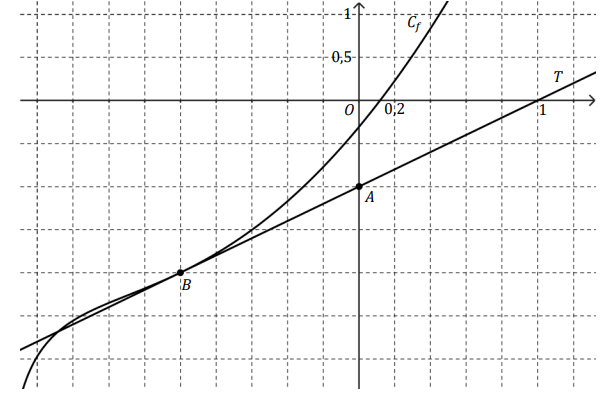
Partie A : exploitation du graphique.
À l’aide du graphique, répondre aux questions ci-dessous.
1. Préciser f(−1) et f
′
(−1).
f(-1) = -2 ; f '(-1) = coefficient directeur de la tangente T soit 1.
2. La courbe Cf est-elle convexe sur son ensemble de définition ? Justifier.
La courbe Cf passe en dessous de sa tangente T pour des valeurs de x inférieures à environ -1,7.
Si la fonction était convexe sur son ensemble de définition, la courbe
Cf serait au-dessus de n'importe quelle tangente sur tout son ensemble
de définition.
3. Conjecturer le nombre de solutions de l’équation f(x) = 0 et donner une valeur arrondie à
10−1 près d’une solution.
Une seule solution voisine de 0,1.
Partie B : étude de la fonction f.
On considère que la fonction f est définie sur ]−2 ; +∞[ par f(x)= x2 + 2x − 1 + ln (x + 2), où
ln désigne la fonction logarithme népérien.
1. Déterminer par le calcul la limite de la fonction f en −2. Interpréter graphiquement ce résultat.
(-2)2+2(-2)-1 =-1 ; en -2, ln(x+2) tend vers -oo ; par somme des limites, f(x) tend vers - oo.
La droite d'équation x = -2 est asymptote.
On admet que en +oo, f(x) tend vers +oo.
.
2. Montrer que pour tout 𝑥 > −2, f
′
(x) =
(2x2+6x+5/ ( x+2) .
f '(x) = 2x+2+1/(x+2) =[(2x+2) (x+2) +1 ] /(x+2) =(2x2+6x+4 +1) / (x+2) =(2x2+6x+5)/ ( x+2) .
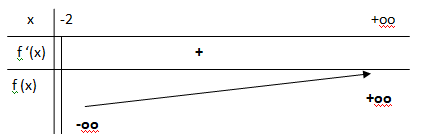
3. Étudier les variations de la fonction fsur ]−2 ; +∞[ puis dresser son tableau de variations
complet.
x+2 est positif.
On cherche les solutions de 2x2+6x+5 = 0.
D = 62-4*5*2 = -4, aucune racine réelle.
2x2+6x+5 > 0.
f '(x) est positive et f(x) est strictement croissante.
4. Montrer que l’équation f(x) = 0 admet une unique solution a sur ]−2 ; +∞[ et donner une
valeur arrondie de a à 10−2 près.
f(x) est continue car dérivable sur ]-2 ; +oo[, et elle est strictement croissante de -oo à +oo.
zéro est une valeur intermédiaire entre -oo et +oo.
D'après le corollaire des valeurs intermédiaires, l'équation f(x) = 0 admet une unique solution sur ]-2 ; +oo[, notée a.
La calculatrice conduit à : 0,115 < a < 0,12.
5. En déduire le signe de f(x) sur ]−2 ; +∞[.
f est à valeurs strictement négatives sur ]-2 ; a[ ;
f est nulle pour x = a.
f est à valeurs strictement positives sur ]a ; +oo[.
6. Montrer que Cf admet un unique point d’inflexion et déterminer son abscisse.
f '(x) étant une fraction rationnelle, est dérivable partout où elle est définie.
f
′
(x) =
(2x2+6x+5)/ ( x+2) .
On pose u = 2x2+6x+5 et v = x+2.
u' = 4x+6 ; v' = 1.
(u'v-v'u) / v2 =[(4x+6)(x+2) -(2x2+6x+5)] /(x+2)2 =(4x2+14x+12-2x2+6x+5) / (x+2)2 =(2x2+8x+7) /(x+2)2.
f "(x) a le signe de 2x2+8x+7.
Recherche des solutions de 2x2+8x+7 =0.
D =82-4 *7*2=8.
x1 =(-8+8½) / 4= -2-2½ /2 < -2 ; x2 =(-8-8½) / 4 = -2+2½ / 2.
f "(x) < 0 sur ]-2 ; -2+2½ /2 [. f(x) est concave sur cet intervalle.
Pour x = -2+2½ /2, f "(x) =0.
f "(x) >0 sur ]-2+2½ / 2 ; +oo[ . f(x) est convexe sur cet intervalle.
f(x) admet un unique point d'inflexion pour x = -2+2½ /2.
Partie C : une distance minimale.
Soit g la fonction définie sur ]−2 ; +∞[ par g(x) = ln(x + 2).
On note Cg sa courbe représentative dans un
repère orthonormé , représentée ci-dessous.
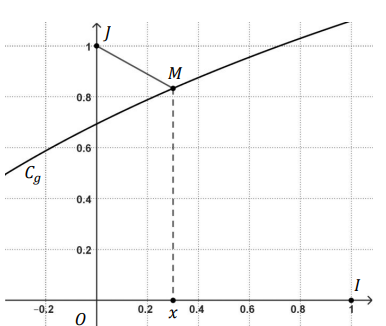
Soit M un point de Cg d’abscisse x.
Le but de cette partie est de déterminer pour
quelle valeur de x la distance JM est minimale.
On considère la fonction h définie
sur ]−2 ; +∞[ par h(x)=JM2
.
1. Justifier que pour tout 𝑥 > −2, on a : h(x) = x2 + [ln(x + 2) − 1]
2
.
J(0 ; 1) : M(x ; ln(x+2)).
JM2 = x2+(ln(x+2)-1)2 .
2. On admet que la fonction h est dérivable sur ]−2 ; +∞[ et on note h′ sa fonction dérivée.
On admet également que pour tout réel x > −2,
h′(𝑥) =
2 f(x) / (x+2) où f est la fonction étudiée en partie B.
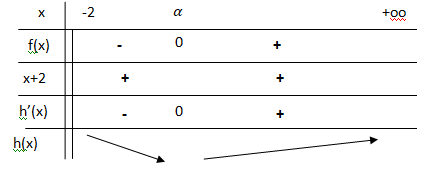
a. Dresser le tableau de variations de h sur ]−2 ; +∞[.
Les limites ne sont pas demandées.
b. En déduire que la valeur de x pour laquelle la distance JM est minimale est a où a est le
nombre réel défini à la question 4 de la partie B.
3. On notera Ma le point de Cg d’abscisse a.
a. Montrer que ln(a + 2) = 1 − 2a − a2
.
a est solution de l'équation f(x) = 0.
x2+2x-1+ln(x+2) = 0 ; ln(x+2) = 1-2x-x2.
a étant solution de cette équation : ln(a + 2) = 1 − 2a − a2
.
b. En déduire que la tangente à Cg au point Ma et la droite (JMa) sont perpendiculaires.
On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont
perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1.
Coefficient directeur de la tangente à Cg au point Ma : g'(a) = 1 /(a+2).
Coefficient directeur de la droite (JMa) :
(yMa-yJ) / (xMa-xJ) =(g(a)-1) / (a-0) =(ln(a+2)-1) / a =(1-2a-a2-1) / a =-2-a.
Le produit de ces deux coefficients directeurs vaut : (-2-a) /(a+2) = -1
La tangente à Cg au point Ma et la droite (JMa) sont perpendiculaires.
Exercice 4. 4 points.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit
être justifiée. Une réponse non justifiée ne rapporte aucun point.
Dans l’espace muni d’un repère orthonormé, on considère les
points suivants : A(2; 0; 0), B(0; 4; 3), C(4; 4; 1), D(0; 0; 4 ) et
H(−1; 1; 2).
Affirmation 1 : les points A, C et D définissent un plan P d’équation 8x − 5y + 4z − 16 = 0. Vrai.
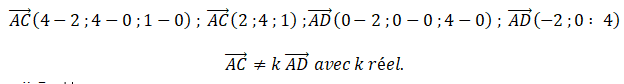
Ces deux vecteurs n'étant pas colinéaires, les points A, C et D ne sont pas alignés ; ils définissent un plan.
Equation de ce plan : ax+ by +cz+d = 0.
A appartient à ce plan : 2a+d = 0 ; a = -0,5d.
D appartient à ce plan : 4c+d=0 ; c = -0,25 d.
C appartient à ce plan : 4a+4b+c+d = 0.
-2d+4b-0,25d+d=0 ; 4b -1,25d ; b = 0,3125 d.
Par suite :-0,5d x+0,3125d y-0,25d z+d = 0.
-0,5x+0,3125y-0,25z+1=0.
-16(-0,5x+0,3125y-0,25z+1) =0
8x-5y+4z-16 = 0.
Affirmation 2 : les points A, B, C et D sont coplanaires. Faux.
Les points A, C et D définissent le plan d'équation 8x-5y+4z-16 = 0.
Si B appartient à ce plan : 8xB-5yB+4zB-16 = 0.
8 *0-5*4+4*3-16 = -24 différent de zéro.
B n'appartient pas au plan (A, C, D).
Affirmation 3 : les droites (AC) et (BH) sont sécantes. Vrai.
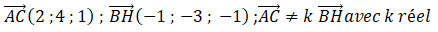
Ces deux vecteurs n'étant pas colinéaires, les droites (AC) et (BH) sont soit sécantes, soit non coplanaires.
Représentation graphique de ces deux droites:
(AC) : { x = 2+2t ; y =4t ; z = t avec t réel }.
(BH) : { x = -s ; y = -3s+4 ; z = -s+3 avec s réel }.
Dans l'hypothèse où les droites sont sécantes :
2+2t = -s ; 4t = -3s+4 = 6+6t+4= 6t+10 ; t =-5 ; par suite s = 8.
z = t = -s+3 conduit à : -5 = -5 vérifié.
L'hypothèse est valide..
On admet que le plan (ABC) a pour équation cartésienne x − y + 2z − 2 = 0.
Affirmation 4 : le point H est le projeté orthogonal du point D sur le plan (ABC). Vrai.
Le point H(-1 ; 1 ; 2) appartient -il au plan (ABC) ?
xH-yH +2zH-2 =-1 -1+4-2 =0.
H appartient donc au plan (ABC).
Le vecteur DH est-il normal au plan (ABC) ?
Coordonnées d'un vecteur normal au plan (ABC) : (1 ; -1 ; 2) d'après l'équation donnée.
Coordonnées du vecteur DH( -1 ; 1 ; -2)
Ces deux vecteurs étant colinéaires le vecteur DH est normal au plan (ABC).
|
ane.
|
|
|