Apprentissage
du saut en parachute, bac centres étrangers 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Au cours de l’une des étapes de sa formation, un
élève parachutiste doit apprendre à évaluer par lui-même la durée au bout de laquelle il doit actionner la
commande de l’ouverture de son parachute, quelques secondes après avoir sauté de
l’avion.
En cas d’urgence, un parachute de secours se déclenche automatiquement.
Mais avant de sauter, l’élève et son moniteur doivent pouvoir
s’entendre parler dans l’avion !
Données :
- Masse de l’élève parachutiste et de son équipement : m = 75,0 kg.
- Intensité du champ de pesanteur g = 9,81 m ⋅ s−2.
Partie 1 – Communication dans l’environnement bruyant de l’avion.
Dans l’avion qui emmène le moniteur et son élève à l’altitude
souhaitée, le niveau d’intensité sonore est L1 = 82 dB.
On estime que, dans le cas de deux émissions sonores simultanées, il
faut que les niveaux d’intensité sonore soient séparés de 8 dB au minimum pour que le son le
plus faible n’empêche pas d’entendre clairement le son le plus fort.
Données :
Le niveau d’intensité sonore L (dB) et l’intensité sonore I sont liés
par la relation :
L = 10 log(I / I0) avec I0 = 1,0 × 10−12 W ∙ m−2, seuil d’audibilité ;
On estime qu’il est nécessaire de crier pour produire un son
d’intensité sonore égale ou supérieure à I𝐶 = 1,0 × 10−3 W ⋅ m−2.
1. Préciser le niveau d’intensité sonore minimal L2 que doit avoir la
conversation entre le moniteur et son élève pour qu’ils puissent s’entendre clairement en
dépit du bruit de l’avion.
L2 = L1+8 = 82+8 = 90 dB.
2. Indiquer, en justifiant, si la gêne occasionnée par le bruit de
l’avion impose ou non au moniteur et à son élève de crier.
I2 = I0 10L2 / 10 =1,0 10-12 x 109 =10-3 W ⋅ m−2.
Il est nécessaire de crier pour s'entendre.
Compte tenu du niveau d’intensité sonore dans l’avion, les pilotes
utilisent des casques d’aviation ANR (pour Active Noise Reduction ou Réduction Active de
Bruit), aussi appelés casques actifs, pour faciliter les communications. Le fonctionnement de
ces casques repose sur une technologie électronique qui permet de capter les bruits
extérieurs via un microphone placé sur la coque du casque, et d'émettre, dans l'écouteur
du casque, un signal qui vient se superposer au bruit de l’avion de façon à le réduire.
3. Nommer le phénomène physique exploité par la technologie ANR.
Interférences destructives des ondes sonores.
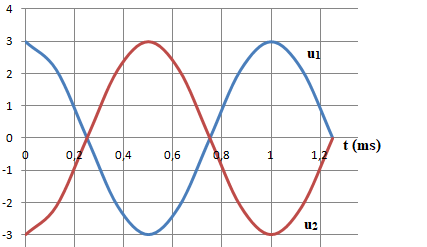
Afin d’illustrer au laboratoire le principe d’un casque ANR, on place
un microphone en face de deux enceintes sonores. La première enceinte produit un son
modélisant le bruit de l’avion par un signal de fréquence unique. Le document 1 donné en
annexe montre
l’évolution temporelle de la tension u1 aux bornes du microphone.
4. Représenter sur le document 1,l’allure du signal que doit produire la deuxième enceinte pour «
supprimer » le son
modélisant le bruit de l’avion.
Partie 2 – Détermination expérimentale de l’altitude au moment de l’ouverture du parachute.
L’élève parachutiste et son moniteur quittent simultanément l’avion en un point A, d’altitude zA = 1 500 m. Tout au long du saut, le moniteur reste à la même altitude que son élève.
Lorsque l’élève ouvre son parachute, le moniteur relève la valeur de l’altitude zB indiquée par son altimètre. Cette valeur sera utile pour le débriefing après le saut.
Le principe de fonctionnement de l’altimètre est basé sur la mesure
d’une variation de pression à partir de laquelle est déduite une
variation d’altitude. Cette partie s’intéresse à un modèle de
détermination d’une variation d’altitude à partir de la mesure d’une
variation de pression.
Données :
- D’après la loi fondamentale de la statique des fluides, la variation
de pression entre les altitudes z et z+h est liée à la variation
d’altitude h par la relation :
p(z)-p(z+h)= r g h
avec p en Pa, h en m, g intensité du champ de pesanteur terrestre et r la masse volumique de l’air en kg ⋅ m−3 ;
- Echelle absolue de température : T (K) = q (°C) + 273,15 ;
- Constante des gaz parfaits : R= 8,314 Pa ⋅ m3 ⋅ mol−1. K−1 ;
- Masse molaire de l’air : M = 29,0 g ⋅ mol−1 ;
- À l’altitude zA = 1 500 m, la valeur de la pression est pA = 845 hPa et celle de la température est q𝐴 = 5,5 °C ;
Dans la situation étudiée, l’air peut être considéré comme un gaz parfait.
5. En utilisant l’équation d’état des gaz parfaits, montrer que la masse volumique de l’air à l’altitude zA = 1 500 m a pour valeur r = 1,06 kg ⋅ m−3.
PV = n RT ; n = m / M ; PV = m RT / M ;
m / V = P M / ( R T) =845 102 x 29,0 10-3 / (8,314 x 278,65)=1,06 kg ⋅ m−3.
On suppose que cette valeur de la masse volumique de l’air est constante pour la hauteur de chute considérée.
Entre le point A et l’ouverture du parachute, l’altimètre a mesuré une différence de pression de 31,8 hPa.
6. Déterminer l’altitude zB qu’afficherait l’altimètre s’il utilisait la loi fondamentale de la statique des fluides.
p(zB)-p(zA)= r g h ; h = p(zB)-p(zA)/( r g) =31,8 102 /(1,06 x9,81) =306 m.
zB =1500-306= 1194 ~1,19103 m.
Remarque
: En pratique, les altimètres utilisent un autre modèle et une autre
relation entre la variation de pression et l’altitude (formule du
nivellement barométrique) car la température ainsi que la masse
volumique de l’air varient avec l’altitude.
Partie 3 – Détermination théorique de l’altitude lors de l’ouverture du parachute.
L’élève parachutiste ainsi que son moniteur quittent simultanément
l’avion en un point A, à un instant pris comme origine des dates (t = 0
s). Lorsqu’ils sautent de l’avion, celui-ci vole horizontalement à
l’altitude zA = 1 500 m avec une vitesse vA = 130 km ⋅ h−1.
L’élève a pour consigne d’enclencher l’ouverture de son parachute après avoir compté 10 secondes.
On étudie le mouvement du système {parachutiste +équipement} avant
l’ouverture du parachute. Cette étude est réalisée dans le référentiel
terrestre considéré comme galiléen.
Dans cette partie, pour modéliser le mouvement du parachutiste, on fait
l’hypothèse que les actions de l’air sont négligeables et que
le mouvement du système est plan.La position du parachutiste est repérée dans le système d’axes (O, x, z), l’origine O étant
prise au niveau du sol qui correspond également ici au niveau de la
mer. Le point A est situé à la verticale du point O sur l’axe (Oz).
7. Indiquer la (ou les) action(s) exercée(s) sur le parachutiste et la (ou les) modéliser par une (ou des) force(s).
L'action de l'air étant néglieable, le parachutiste n'est soumis qu'à son poids ( verticale, vers le bas, valeur mg ).
8. En déduire, en justifiant, les coordonnées théoriques du vecteur accélération ax (t) et az (t) et les expressions des coordonnées vx (t) et vz (t) du vecteur vitesse du centre de masse du système.
La seconde loi de Newton écrite dans ce repère conduit à : ax (t)=0 et az (t)= -g.
Le vecteur vitesse est une primitive du vecteur accélération.
vx (t)=vA = 130 /3,6 =36,1 m /s et vz (t) = -g t= -9,81 t.
9. Montrer que les équations horaires du mouvement du parachutiste dans le repère (O, 𝑥, 𝑧) sont modélisées par :
x(t) =vAt ; z(t) =-½gt2 + zA.
avec 𝑡 en seconde, vA en mètre par seconde et x(t), z(t) et zA en mètre.
Le vecteur position est une primitive du vecteur vitesse et la position initiale A a pour coordonnées (0 ; zA = 1500 ).
Donc :
x(t) =vAt ; z(t) =-½gt2 + zA.
10. Déterminer l’altitude théorique zC à laquelle le parachutiste devrait ouvrir son parachute sachant que cette ouverture doit avoir lieu 10 s après le saut.
t = 10 ; zC = -9,81 / 2 x102 +1500 =1009 ~1,0 103 m.
L’altimètre du moniteur indique zB = 1,2 × 103 m lorsque l’élève ouvre son parachute.
11. Proposer au moins deux raisons pour expliquer la différence entre la valeur mesurée zB et la valeur calculée zC.
Les frottements sur les couches d'air doivent être pris en compte.
Le mouvement n'est peut être pas plan ; la chute n'est pas verticale.
|
...
|
....
|
Partie 4 – Parachute de secours.
Si le parachute ne s’ouvre pas, la vitesse de chute peut atteindre 200 km ⋅ h−1.
Un déclencheur de sécurité doit alors libérer le parachute de secours.
Pour être pleinement fonctionnel, il doit respecter les deux conditions
suivantes :
- Il doit entrer en action avant que l’altitude ne devienne inférieure à 320 m (condition sur l’altitude).
- Il doit permettre de passer de 200 km ⋅ h−1 à moins de 20 km ⋅ h−1 en 10 s (condition sur la vitesse).
Une fois le parachute de secours ouvert, les frottements dans l’air ne sont plus négligeables.
Ils sont modélisés par une force, notée f, de sens opposé au vecteur
vitesse et de valeur proportionnelle au carré de la vitesse :
f = k v2 ,k est appelé coefficient de frottement.
Cette modélisation des frottements a permis de tracer le graphique
représentant l’évolution de la vitesse du centre de masse du système
{parachutiste + équipement}. Sur ce graphique, l’origine des dates
correspond à l’ouverture du parachute de secours.
Dans la suite, le mouvement est considéré vertical depuis la date
d’ouverture du parachute de secours jusqu’à la date d’arrivée sur le
sol.
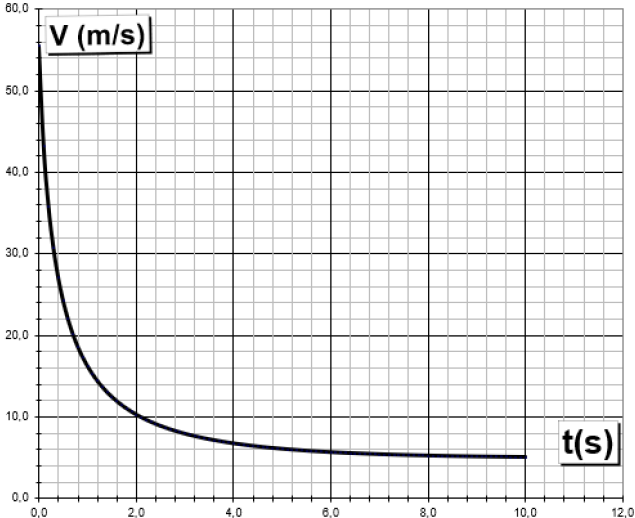
12. Montrer que la modélisation rend bien compte de la condition de fonctionnement du parachute de secours portant sur la vitesse.
La vitesse décroît de 55,5 m /s ( 200 km / h) à 5 m /s ( 20 km / h) en 10 s.
On cherche à déterminer les caractéristiques du vecteur accélération 2
s après le déclenchement du parachute de secours. Pour cela, on doit
d’abord retrouver la valeur du coefficient de frottement k utilisée
dans cette modélisation.
13. Écrire la relation entre le vecteur accélération a du système, et les forces modélisant les actions s’exerçant sur le système.
Le système est soumis à son poids et à la force de frottement.
Ecrire la seconde loi de Newton sur un axe vertical orienté vers le haut : m a = -mg +f = -mg +kv2.
a = -g +k / m v2.
Après la date t = 9 s, on peut considérer que la vitesse prend une valeur constante vf.
14. Écrire, à
partir de cette date, la relation entre les valeurs des forces et en
déduire l’expression du coefficient de frottement k en fonction de m, g
et vf .
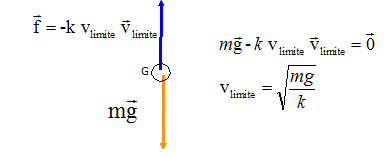
Le mouvement étant rectiligne uniforme, la première loi de Newton conduit à : mg = kvf2.
k = mg / vf2.
15. En déduire la valeur du coefficient de frottement k choisi pour la modélisation. Préciser l’unité de k.
Le graphe donne vf ~5 m / s ; k = 75 x9,81 / 52 ~29,4 kg m-1.
kg m s-2 / (m2s-2) soit kg m-1.
16. Donner les caractéristiques (sens, direction et valeur) du vecteur accélération du système à la date t = 2 s . Commenter.
v(t=2) = 10 m /s ;
a = -g +k / m v2 = -9,81 +29,4 / 75,0 x102 = 29,4 m s-2.
Vecteur accélération : verticale, vers le haut ( sens de l'axe Oz) , valeur 29,4 m s-2.
Le vecteur accélération et le vecteur vitesse sont de sens contraire, le mouvement est décéléré.
|
|