Mathématiques
: lois de probabilités.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Loi uniforme.
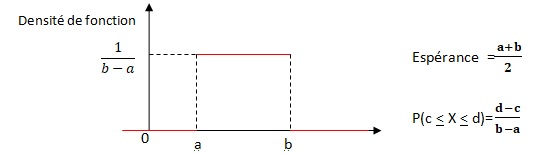
Sofia utilise le bus pour se rendre au cinéma. La durée du
trajet entre son domicile et le cinéma (exprimée en minutes) est
modélisée par la variable aléatoire TB qui suit la loi uniforme sur [12
; 15].
1. Démontrer que la probabilité que Sofia mette entre 12 et 14 minutes est de 2 / 3.
P(12 < TB < 14) =(14-12) / (15-12) = 2 / 3.
2. Donner la durée moyenne du trajet.
(15+12) / 2 = 13,5.
Loi exponentielle.
Loi de durée de vie sans vieillissement.
La durée de vie, en années, d’un composant électronique fabriqué dans
cette usine est une variable aléatoire T qui suit la loi exponentielle
de paramètre l (où
l est
un nombre réel strictement positif ). On note f la fonction densité
associée à la variable aléatoire T .
1. La courbe
représentative C de la fonction f est donnée ci-dessous.
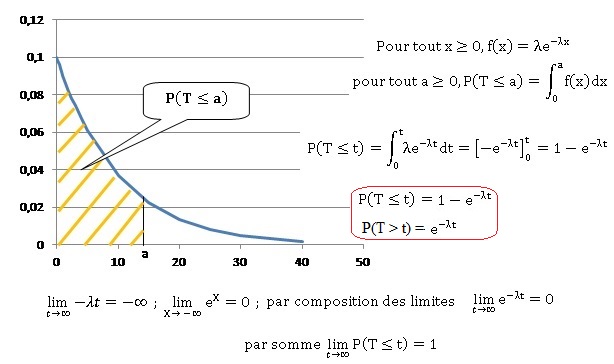 2.
On suppose que P(T < 7) = 0,5. Déterminer l à 10−3 près.
2.
On suppose que P(T < 7) = 0,5. Déterminer l à 10−3 près.
1-exp(-7 l)=0,5 ;
exp(-7
l)
=0,5 ; -7
l
=ln0,5 = -ln2 ; l = ln2 / 7 ~0,099.
3.
Dans cette question on prend λ = 0,099 et on arrondit les résultats des
probabilités au centième.
a. On choisit au
hasard un composant fabriqué dans cette usine. Déterminer la
probabilité que ce composant fonctionne au moins 5 ans.
P(T > 5)=P(t>5) = 1- (1-exp(-5l)) = exp(-5l) = exp(-5x0,099)~0,61.
b.
On choisit au hasard un composant parmi ceux qui fonctionnent encore au
bout de 2 ans.
Déterminer la probabilité que ce composant ait une durée de vie
supérieure à 7 ans.
La loi exponentielle modèlise la durée de vie d'un phénomène sans
mémoire. Le fait que le phénomène ait duré pendant t heures ne change
rien à son espérance de vie à partir de l'instant t.
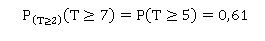
c. Donner
l’espérance mathématique E(T ) de la variable aléatoire T à l’unité
près. Interpréter ce résultat.
E(T) = 1 / l = 1
/0,099 ~10,1 ans.
La durée de vie moyenne d'un composant est d'environ 10 ans.
|
Loi binomiale.
Epreuve de Bernoulli : expérience aléatoire qui admet deux issues : succès de probabilité p ou échec de probabilité q = 1-p.
Exemple : on lance une pièce ( pile ou face).
Schéma de Bernoulli d'ordre n : répétition de n épreuves de Bernoulli identiques et indépendantes.
Espérance : E = n p.
Variance V = n p (1-p).
Un joueur s'initie à un jeu en effectuant plusieurs parties
successives. Pour la première partie, les probabilités de gagner et de
perdre sont égales. Pour les parties suivantes, on suppose que si une
partie est gagnée, alors la probabilité de gagner la suivante est 0,6.
Si la partie est perdue, la probabilité de perdre la suivante est 0,7.
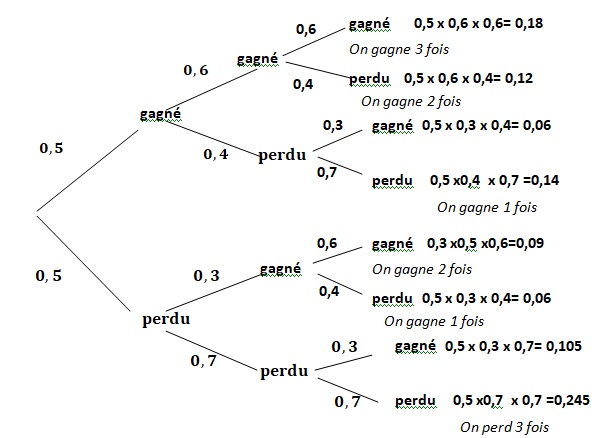
Au bout de deux parties :
1. Représenter l'ensemble des issues de ces expériences par un arbre.
2. Déterminer les probabilités suivantes :
- On gagne deux fois ; - on perd deux fois ; on gagne une seule fois.
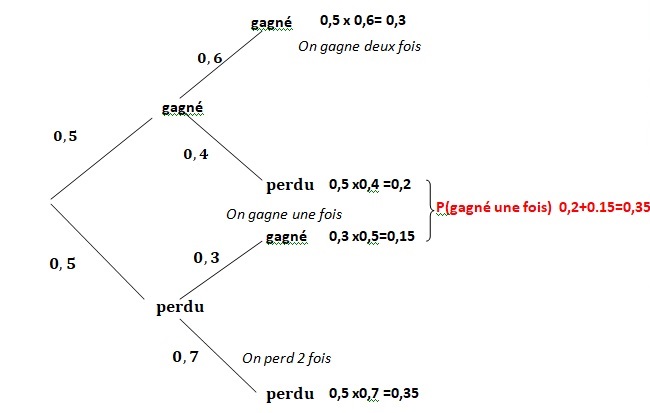
Mêmes questions au bout de trois parties.
Un jeu de hasard est paramétré de la façon suivante :
Si le joueur gagne une partie, la probabilité qu'il gagne la partie suivante est 0,25.
Si le joueur perd une partie, la probabilité qu'il perde la partie suivante est 0,5.
La probabilité de gagner la première partie est 0,25.
Pour tout entier n non nul, on note Gn l'événement " la nième partie est gagnée" et on note pn la probabilité de cet événement. On a donc p1 = 0,25.
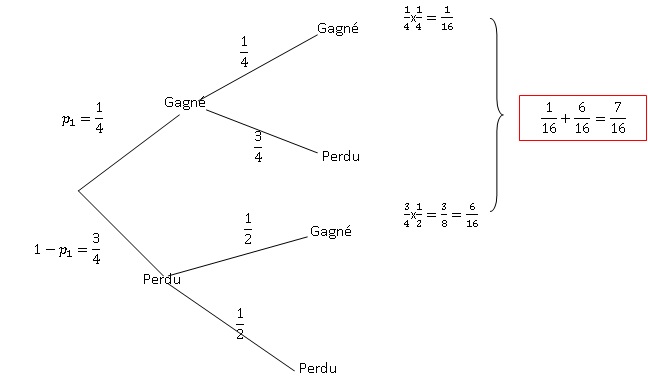
1. Montrer que p2 = 7 / 16.
2. Montrer que pour tout entier n non nul, pn+1 = -pn / 4 +0,5.
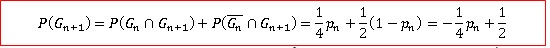
3. On obtient ainsi les premières valeurs de pn :
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
pn
|
1
|
0,4375
|
0,3906
|
0,4023
|
0,3994
|
0,4001
|
0,3999
|
Quelle conjecture peut-on émettre ?
La limite de pn est 0,4.
4. On définit pour tout entier naturel non nul, la suite (un) par un= pn-0,4.
a. Démontrer que cette suite est géométrique et donner la raison.
un+1= pn+1-0,4= -pn / 4 +0,5-0,4=0,1-pn / 4 = (0,4-pn) / 4 = -0,25 un.
La suite est géométrique de raison -0,25 et de premier terme p1-0,4 = 0,25-0,4 = -3 / 20.
b. En déduire que pour tout entier naturel n non nul, pn = 0,4 -3 / 20 (-0,25)n-1.
un = -3 / 20 x (-0,25)n.
pn = un +0,4 = 0,4 -3 / 20 (-0,25)n-1.
c. La suite (pn) converge t-elle ? Interpréter.
Quand n tend vers plus l'infini, (-0,25)n-1 tend vers zéro et la suiteconverge vers 0,4.
Au bout d'un grand nombre de parties, la probabilité de gagner est de 0,4.
|
|
Loi normale.
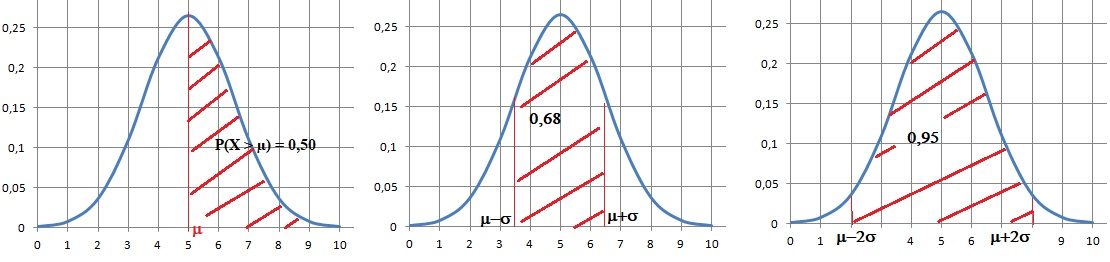
On modélise l’épaisseur en millimètre d’un carreau pris au hasard par
une variable aléatoire X qui suit une loi normale d’espérance μ = 11 et
d’écart type σ.
Un carreau est commercialisable si son épaisseur mesure entre 10,1 mm et 11,9 mm.
On sait que 99 % des carreaux sont commercialisables.
1. Démontrer que P(X < 10,1) = 0,005.
;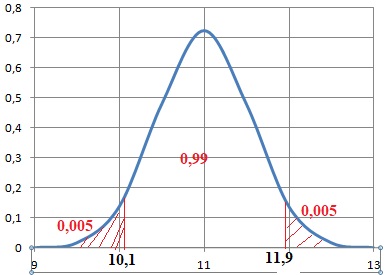
P(X > 11,9) = P(X <10,1) =(1-0,99) / 2 = 0,005.
2. On introduit la variable aléatoire Z telle que Z =(X −11) /σ.
a. Donner la loi suivie par la variable aléatoire Z.
Z suit la loi normale centrée réduite N(0 ; 1).
b. Démontrer que P(Z < -0,9 / s) =0,005.
c. En déduire la valeur de σ arrondie au centième.
On effectue un changement de variable : Z =(X −11) /σ.
Z suit la loi normale centrée réduite N(0 ; 1).
P(10,1 < X < 11,9) = 0,99 ; P(10,1-11 < X-11 < 11,9-11) = 0,99 ;
P(-0,9 < X-11 < 0,9) = 0,99 ;
P(-0,9/ s < (X-11) / s < 0,9 / s) = 0,99 ;
P(-0,9/ s < (Z < 0,9 / s) = 0,99 ;
2P(Z < 0,9 / s)-1 = 0,99 ;
P(Z < 0,9 / s) =0,995 ;
P(Z < -0,9 / s) =1-0,995 =0,005
s = 0,35.
Une tablette de chocolat doit peser 100 grammes avec une tolérance de
deux grammes en plus ou en moins. Elle est donc mise sur le marché si
sa masse est comprise entre 98 et 102 grammes. La masse (exprimée en
grammes) d’une tablette de chocolat peut être modélisée par une
variable aléatoire X suivant la loi normale d’espérance µ = 100 et
d’écart-type s =
1. Le réglage des machines de la chaîne de fabrication permet de
modifier la valeur de s.
1. Calculer la
probabilité de l’évènement M : « la tablette est mise sur le marché ».
P(X < 98) = 0,0228 ; P( X >
102) =0,0228.
Probabilité que la tablette soit mise sur le marché =1-0,0228-0,0228=0,9544.
2. On souhaite
modifier le réglage des machines de telle sorte que la probabilité de
cet évènement atteigne 0,97.
Déterminer la valeur de s
pour que la probabilité de l’évènement « la tablette est mise sur le
marché » soit égale à 0,97.
On effectue un changement de variable en posant : Z =( X-µ) / s
;
Z suit la loi normale centrée réduite N(0 ; 1).
P(98 < X < 102) = 0,97 ; P(98-100 < X-100 < 102-100) = 0,97 ;
P(-2 < X-100 < 2) = 0,97 ;
P(-2/ s < (X-100) / s < 2 / s) = 0,97 ;
P(-2/ s < (Z < 2 / s) = 0,97 ;
2P(Z < 2 / s)-1 = 0,97 ;
P(Z < 2 / s) =0,985 ;
P(Z < -2 / s) =1-0,985 =0,015
2
/ s = 2,17,
d'après les tables ou la calculatrice; s
= 2 / 2,17 =0,9216.
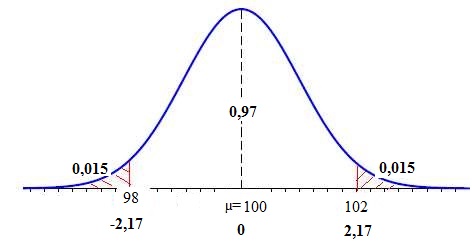
|
Intervalle de fluctuation asymptotique.
Dans cette étude de marché, il est précisé que 46,8 % des consommateurs en France privilégient des produits locaux. Le commerçant constate que parmi ses 2 500 clients, 1 025 achètent régulièrement des produits locaux.
Sa clientèle est-elle représentative des consommateurs en France ?
On teste l'hypothèse p = 0,468 sur un échantillon de taille n = 2500.
n = 2500>30, np = 2500×0,468 = 1170 >5 et n(1−p) = 2500×0,532 = 1330 >5.
Les conditions pour établir un intervalle de fluctuation asymptotique au seuil de 95 % sont requises :
1,96 ( p(1-p) / n)½ = 1,96 x(0,468 x0,532/2500)½ =0,0196.
Intervalle de fluxtuation : [0,468 -0,0196 ; 0,468 +0,0196] soit [0,448 ; 0,488].
La fréquence 1025 / 2500 = 0,41 n'appartient pas à cet intervalle.
Sa clientèle n'est pas représentative des consommateurs en France.
La
société annonce un taux de satisfaction de 85 % pour ces clients ayant
appelé et obtenu un opérateur. Une association de consommateurs
souhaite vérifier ce taux et interroge 1303 clients. parmi celles-ci
1150 se disent satisfaites. Que pensez-vous du taux de satsifaction
annoncé par la société ?
n =1303 >30 ; p = 0,85 soit np = 1303 x0,85=1107,55 > 5.
nq = n(1-p) = 1303 x0,15 = 195,45 >5.
Au seuil de confiance de 95%, on détermine un intervalle de fluctuation asymptotique :
1,96 (pq / n)½ = 1,96 x(0,85 x0,15 /1303)½ =0,0194.
[0,85-0,0194 ; 0,85+0,0194 ] soit [0,830 ; 0,869].
La fréquence observée est égale à 1150 /1303 ~0,883, n'appartient pas à l'intervalle de fluctuation.
Le taux de satisfaction annoncé est trop faible, au risque de 5 %.
Intervalle de confiance.
Des
améliorations apportées à la chaîne A ont eu pour effet d’augmenter la
proportion p de composants sans défaut. Afin d’estimer cette
proportion, on prélève au hasard un échantillon de 400 composants parmi
ceux fabriqués par la chaîne A. Dans cet échantillon, la fréquence
observée de composants sans défaut est de 0,92.
1. Déterminer un intervalle de confiance de la proportion p au niveau de confiance de 95%.
Taille de l'échantillon n = 400, supérieur à 30.
Proportion de composants sans défaut p = 0,92 ; q = 1-p = 0,08.
np = 368, valeur supérieure à 5 ; nq = 32, valeur supérieure à 5.
Les
conditions sont requises pour établir un intervalle de confiance de la
proportion p au seuil de 95 % de l'échantillon de taille n = 400.
1 / 400½= 0,05 ; intervalle de confiance [0,92 -0,05 ; 0,92 +0,05] soit [0,87 ; 0,97].
2. Quelle
devrait être la taille minimum de l’échantillon pour qu’un tel
intervalle de confiance ait une amplitude maximum de 0,02 ?
2 x(1/n)½ =0,02 ;(1/n)½ =0,01 ; 1/n = 10-4 ; n=10000.
|
|