Mathématiques, école de santé des armées ESA 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... QCM 1. La fonction f(x)  définie sur R est : A. Impaire. B. Paire. C. Bornée. Vrai. D. Aucune des réponses précédentes. QCM 2. Calcul de limite quand x tend vers zéro. A. 1. B. 0. Vrai. C. +oo. D. -1. QCM 3. Calcul de limite. A. -oo B. +oo. C. 0. Vrai. D. 0,5. QCM 4. Soit une fonction f telle que f(1) = 3 et f '(1) = -1. La tangente à la courbe représentative de la fonction f au d'abscisse 1 a pour équation : A. y = -x+3. B. y = -x+4. Vrai. C. y = x-2. D. y = 3x-4 y = f '(1) x + b ; y = -x+b ; 3 = -1+b ; b = 4. QCM 5. Le nombre de solution dans R de l'équation x+sin x = 1 est : A. zéro. B. une infinité. C. une. Vrai. D. deux. QCM 6. L'ensemble des solutions de l'équation 2 e2x+3ex-5=0 est : A. aucune. B. zéro. Vrai. C.  1. D. 1 et -2,5. On pose X = ex >0. 2X2+3X-5 = 0. Discriminant D = 32-4*(-5)*2=49 = 72. Solution retenue : X1 = (-3 +7) / 4 =1 ; x = 0. QCM 7. Deux stéréoisomères ont : A. 3. B. -1. C. 0. D. -3. Vrai. QCM 8. L'ensemble des solutions de l'équation ln(x-1) = ln(1-2x) =0 est : A. -2 /3. B. aucune. Vrai. C. 0. D. 2 / 3. x-1 >0 soit x >1 et 1-2x >0 soit x < 0,5. Impossible. QCM 9. l'ensemble de définition de la fonction f définie par f(x) =ln(e2x-1-2) est : A. ]0,5 ln(3) ; +oo[ B. ]0 ; +oo[ C. ](1 + ln(2)) / 2 ; +oo[. Vrai. D. ]2 ; +oo[ e2x-1-2 >0 ; e2x-1> 2 ; 2x-1 > ln(2) ; 2x >ln(2)+1. QCM 10. A. 4.  Vrai. B. ln(3) / 4. C.  7 D. 2e2. ... .... QCM. 11. Soit la suite géométrique (un) de raison q et de premier terme u1 = 18 telle que u1 xu2 xu3 = 216, alors : A. q = 1 /3. Vrai. B. q = 1 /2 C. q =2 D. q = -1 /3. u2 = 18 q ; u3 = 18 q2 ; 216 = (18 q)3 ; 6 =18 q ; q = 1 /3. QCM 12. 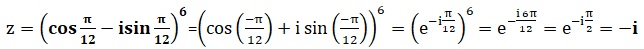Soit le nombre complexe z défini par : A. z=0. B. z=1. C. z=-i. Vrai. D. z= i. QCM 13. 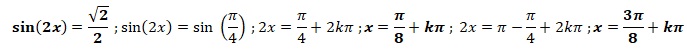L'équation suivante équivaut à : Réponse A. QCM 14. L'ensemble des points M tels que 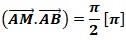 où A et B sont deux points distincts, est : A. Le cercle de diamètre [AB] privé du point A. B. La médiatrice du segment [AB]. C. La perpenficulaire à [AB] passant par le point A, privée du point A. Vrai. D. Le cercle de centre A et de rayon [AB]. QCM 15 . Dans un repère orthonormé de l'espace, on considère les points A(-1 ; 0 ; -2), B(-1 ; -3 ; -5), C(2 ; 1 ; 1) et D(3 ; -2 ; x). Les droites (AB) et (CD) sont orthogonales pour x  égal à : A. -2. B. 0. C. 4. Vrai. D. 1. 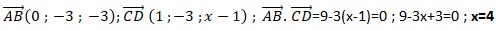QCM 16 . Soit deux événements A et B d'un même univers tels que P(A n B) = 1 / 6 et PA(B) = 1 /4, alorsP(A) est égale à : A. 2 /3. Vrai. B. 1 /24. C. 1 /12. D. 1,5. PA(B) =P(A n B) /(P(A)  ; P(A) =P(A n B) / PA(B) = 4 /6 = 2 /3. QCM 17. La durée de vie en années d'un appareil médical est modélisée par une variable aléatoire T qui suit une loi exponentielle de paramètre l. Sachant que la durée de vie mpyenne de cet appareil est de 10 ans, alors l est égal à : A. 10. B. e-10. C. 0,1. Vrai.(l = 1 /10) D. 1. QCM 18. 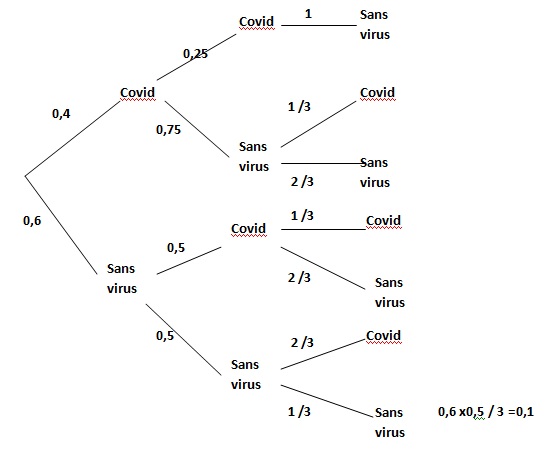On a 5 tubes à essai indiscernables de 5 personnes testées. Deux contiennent le virus Covid 19. Trois ne le contiennent pas. On tire au hasard successivement et sans remise 3 tubes. La probabilité d'obtenir 3 tubes sans virus est : A. 1 /10. Vrai B. 1 /3. C. 1 /40 D. (3 /5)3. 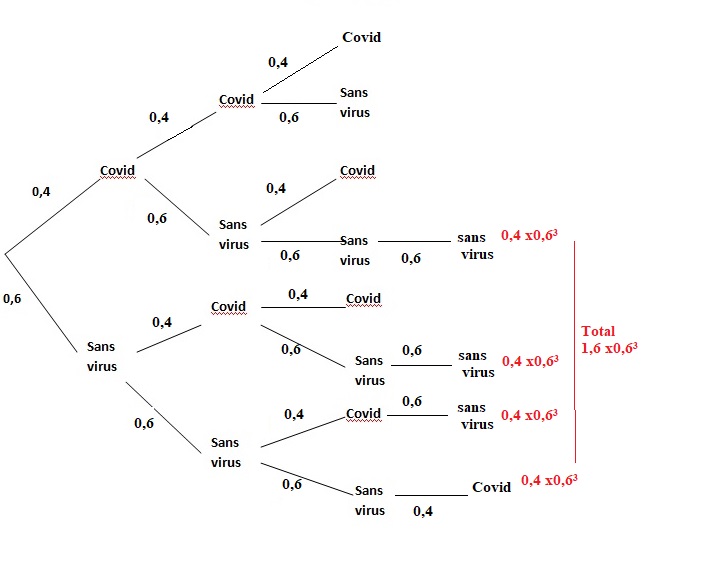QCM 19 . On a 5 tubes à essai indiscernables de 5 personnes testées. Deux contiennent le virus Covid 19. Trois ne le contiennent pas. On tire au hasard un tube, on le teste, on le remet. On procède ainsi à 4 tirages. La probabilité d'obtenir exactement 3 tubes sans virus est : A. (3 / 5)4. B. 4 x3 /5 x 2 /5. C. 4 x(3 /5)3 x2 /5. Vrai. D. (3 /5)3 x2 /5. 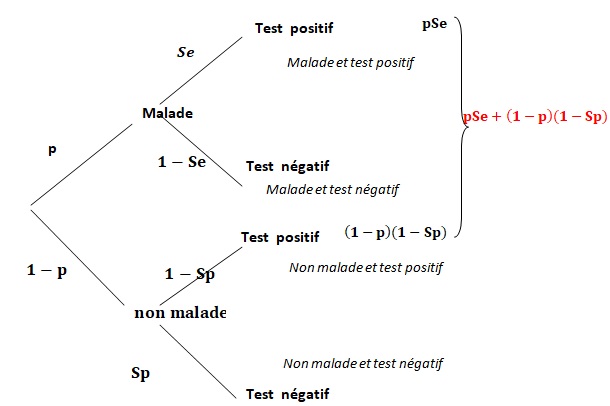QCM 20. Le test gold standard permet de déterminer la probabilité p qu'un individu soit malade dans la population. Comme on ne peut pas tester toute la population ( pour des raisons de coût ), on utilise un test diagnostique, dont les valeurs informationnelles se déclinent ainsi : La sensibilité Se qui est la probabilité qu'un individu d'une population testée soit positif au test diagnostique sachant qu'il est réellement malade. La sensibilité Sp qui est la probabilité qu'un individu d'une population testée soit négatif au test diagnostique sachant qu'il n'est pas réellement malade. On appelle valeur prédictive positive de ce test diagnostique, notée VPP, la probabilité qu'un sujet soit réellement malade sachant qu'il est positif au test diagnostique. Elle vaut : A. (1-p)Se /[pSe +(1-p)(1-Sp)]. B. pSe / ./[pSe +(1-p)(1-Sp)]. Vrai C. pSp / ./[(1-p)Se +p(1-Sp)]. D. pSp / ./[pSp +(1-p)(1-Se)].

menu