....
|
L'échographie.
33. Définir une onde mécanique longitudinale.
Une
onde mécanique est la propagation d'une perturbation dans un milieu
matériel avec transport d'énergie, sans transport de matière. L'onde
est longitudinale si la direction de propagation de l'onde et la
direction de la perturbation sont identiques.
34. Quelle est la fréquence minimale d'une onde ultrasonore ?
20 kHz.
35. Lister les prérequis nécessaires afin de pouvoir étudier le principe de l'échographie en classe.
Ondes sonores : relation vitesse, durée, distance parcourue.
Signaux sinusoïdaux : fréquence, période.
Utilisation de l'ocilloscope.
36. Proposer une expérience permettant de modéliser le principe de l'échographie.
On peut modéliser un examen échographique par un
dispositif expérimental où la sonde joue le rôle d'émetteur et de
récepteur. L'expérience est réalisée dans l'air . L'émetteur E émet des
salves ultrasonores. Une paroi réfléchissante ( jouant le rôle de
l'organe) réfléchit l'onde incidente détectée par le récepteur R.

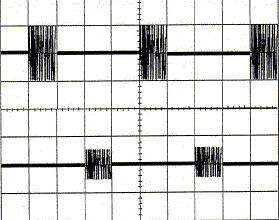
L'oscillogramme permet d'observer le signal de
l'onde émise et le signal de l'onde réfléchie, cette dernière
visualisée dans la partie inférieure de l'écran. La base de temps de
l'oscilloscope vaut 1 ms/div.
37. Comment définir le phénomène de diffraction ?
Le
phénomène de diffraction se produit avec toutes les ondes lorsque que
celle-ci rencontre une fente ( ou l'obstacle ) dont les dimensions sont
du même ordre de grandeur que la longueur d'onde.
Diffraction des ondes sonores par une porte ou une fenètre ; diffraction de la houle à l'entrée d'un port.
La direction de propagation de l'onde est modifiée.
38. Quel est la taille du foetus ?
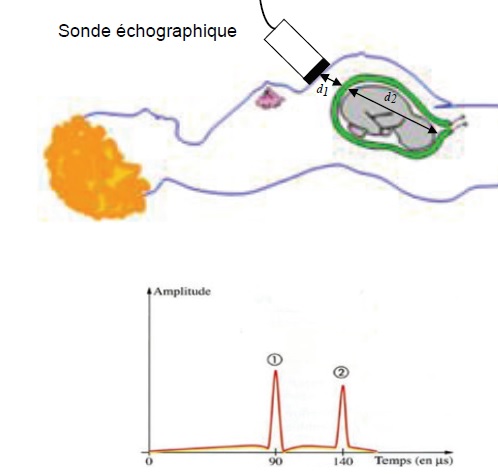
Célérité de l'onde dans les tissus : c = 1,5 103 m /s.
Première reflexion des ondes sur la paroi avant du foetus : 2 d1 = 1,5 103 x90 10-6 ; d1 = 0,0675 m.
Seconde reflexion sur l'autre extrémité du foetus : 2 (d1 +d2)= 1,5 103 x140 10-6 ; d1 +d2= 0,105 m.
d2 = 0,105-0,0675=0,0375 m =3,75 cm.
39. Qu'est-ce qu'un évaluation formative ?
C'est une évaluation qui détecte les difficultés de l'élève afin de lui
venir en aide ( remédiation) : modification des conditions
d'apprentissage, rytme de la progression.
40. Comment les compétences Analyser-Raisonner et Communiquer peuvent être évaluées ici ?
Analyser-Raisonner : l'onde ultrasonore se réfléchit partiellement en rencontrant des tissus de nature différente.
Les temps détectés correspondent à un aller -retour.
Utiliser la relation entre distance, célérité et durée.
Communiquer : conduite des calculs conduisant à la dimension du foetus.
41. Justifier de l'utilisation du gel lors d'une échographie.
Un gel permet de remplacer l'interface air-peau (eau) par les deux interfaces air-gel et gel-tissus (eau) : les ondes sont ainsi mieux transmises.
Scintigraphie thyroïdienne.
42. Donner la composition d'un noyau d'iode 131.
Le noyau d'ode 13153 I compte : 53 protons ; 131-53 = 78 neutrons.
43. Ecrire l'équation de désintégration de l'iode 131.
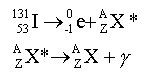
émision
d'électrons et de rayons gamma.
conservation de
la charge : 53 = -1 + Z d'où Z= 54
conservation du
nombre de nucléons : 131 = 0 +A d'où A = 131
X est un isotope
du xénon.
44. Calculer en J et en keV, l'énergie E libérée au cours de cette désintégration.
Défaut de masse =m(13154Xe) +m(ß-) -m(13153I)=130,905 072 +0,000 549 -130,906 114 =-0,000493 u.
1 u = 1,6605 10-27 kg ;
0,000493 x1,6605 10-27 =8,186 265 10-31kg.
E = 8,186 265 10-31 x(3,00 108)2 =7,367 10-14 J.
7,367 10-14 /(1,6 10-19)=4,60 105 eV = 460 keV.
Cette désintégration s'accompagne de l'émission dun rayonnement gamma d'énergie E' = 364 keV.
45. Quelle est l'origine de ce rayonnement ?
Le noyau fils de Xenon est dans un état excité. Il revient à l'état fondamental en émettant un rayonnement gamma.
46.Calculer sa longueur d'onde l.
E'=364 103x1,6 10-19 = 5,824 10-14 J.
l = h c / E' =6,63 10-34 x3,00 108 / (5,824 10-14) = 3,42 10-12 m.
On administre à un patient une dose d'iode 131(t½ = 8,02 jours) d'activité initiale A0 = 4 MBq par voie intraveineuse afin de réaliser une scintigraphie thyroïdienne.
47. Déterminer le nombre N0 de noyaux d'iode 131 dans la dose.
Constante radioactive l = ln2 / t½ = ln2 /(8,02 x24 x3600) =1,00 10-6 s-1.
N0 = A0 / l = 4 106 / (1,00 10-6)=4,0 1012 noyaux.
48. Etablir la relation entre N0, N, t½ et t. N : nombre de noyaux à la date t.
dN /dt = - l N ; dN /dt + l N =0.
N(t) = Cste e-lt ; N0 = Cste ; N(t) = N0 e-lt ;
ln(N(t)) = ln(N0) -lt = ln(N0)-ln(2) t / t½ =ln(N0)-ln(2t / t½) = ln(N0 / 2t / t½).
N(t)=N0 / 2t / t½.
49. Tracer la courbe N(t). La légender.
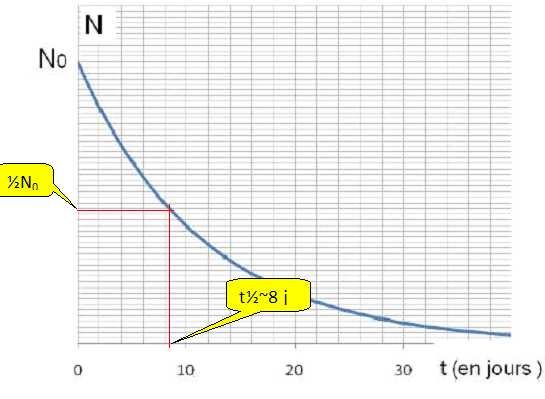
50. Au bout de combien de temps peut-on considérer que l'iode a presque totalement disparu du corps du patient ?
A t > 18 t½, soit environ 64 jours, il n'y a plus de danger.
51. L'iode 123 ( t½
= 13,3 h) peut être également utilisé pour réaliser une scintigraphie.
Indiquer un avantage qu'il représente par rapport à l'iode 131.
L'iode 123 a pratiquement disparu de l'organisme au bout de 8 x13,3 h soit 4,4 jours, au lieu de 64 pour l'iode 131.
On souhaite mettre en évidence les deux isotopes de l'iode cités précédemment à l'aide d'un spectrographe de masse.
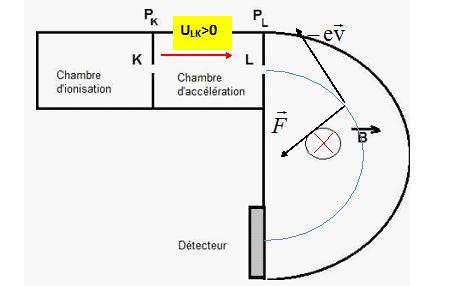
52. Préciser le signe de la tension ULK en justifiant.
La chambre d'ionisation conduit aux ions123I- et 131I-.
Les ions doivent être accélérés entre K et L. Ils sont soumis à la
seule force électrique entre K et L. Le travail de cette force doit
être moteur: W = -eUKL >0 soit UKL < 0 ou ULK >0.
53. Déterminer les valeurs des vitesses de ces ions au point L. ULK = 5000 V.
Ecrire le théorème de l'énergie cinétique entre K et L : ½m(131I-)v2L(131I-) -0=
eULK.
vL(131I-) =
(2eULK / m(131I-))½
.
m(131I-)
=130,906*1,66 10-27 =2,173 10-25 kg.
vL(131I-)
=(2*1,6 10-19 *5000 / (2,173 10-25))½
=8,58 104 m/s.
m(123I-)
=122,906*1,66 10-27 =2,040 10-25 kg.
vL(131I-)
=(2*1,6 10-19 *5000 / (2,040 10-25))½
=8,86 104 m/s.
54.
Représenter le vecteur champ magnétique B supposé uniforme dans le
demi-disque, afin que ces ions puissent atteindre le détecteur.
Voir figure ci-dessus.
55. Quel est la nature du mouvement des ions dans la zone où règne ce champ magnétique.
Le poids des ions est négligeable devant la force magnétique. La force
magnétique, perpendiculaire à la vitesse, ne travaille pas. La valeur
de la vitesse de l'ion rest constante. Le mouvement est uniforme.
56. Etablir l'expression du rayon R de la trajectoire d'un ion.
Dans le repère de Frenet écrire la seconde
loi de Newton sur l'axe n.
La particule chargée n'est soumise qu'à la
force de Lorentz, centripète.
d'où evB= mv
2/ R soit R =
mv /(eB).
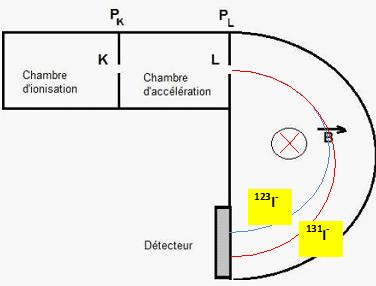
57. Pour quel ion , R est-il le plus important ?
or v =[2 e U0 /
m]½ ;
R =[2 m U0
/ (eB2)]½.
R est constant : la trajectoire est un
cercle.
R(131I-) / R(AI-) =[m(131I-) / m(AI-)]½.
A la masse la plus grande correspond le plus grand rayon.
|