Influence
de l'épaisseur des vêtements sur la protection du froid. Concours CAPLP
2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Modélisation du corps humain.
Deux protocoles expérimentaux différents :
dans les deux cas, on remplit préalablement les flacons d'eau chaude ;
le premier groupe relève les température à l'aide d'une sonde à
l'intérieur des flacons entourés de tissus ; le second les a relevées à
l'aide d'un thermomètre infrarouge à la surface des flacons entourés de
tissus.
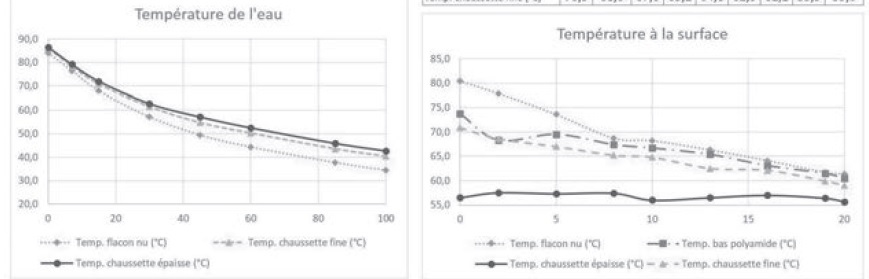
1. Interpréter ces résultats.
La température de l'eau décroît lentement au cours du temps du fait des
échanges thermiques avec l'extérieur. La décroissance est plus rapide
que le flacon est moins isolé thermiquement. Les échanges thermiques se
font essentiellement par conduction à travers la paroi du flacon et
l'isolant et par convection à l'intérieur de l'eau.
2. Justifier l'intérêt de laisser le groupe 2 réaliser le protocole.
La température de surface d'un liquide est-elle très différente de la température relevée au sein du liquide ?
3. Le
groupe 2 déclare " nous avons dû nous tromper car les températures avec
la chaussette épaisse sont très inférieures aux autres". Que répondre ?
En
présence de chausette épaisse, la température au sein du liquide est
d'environ 3 à 4 °C supérieure à celle du liquide contenu dans le flacon
nu. En surface, l'évaporation est plus importante si la température du
liquide est plus élevée. L'évaporation est endothermique, elle puise de
l'énergie dans l'air. L'air et la surface du liquide se refroidissent.
Dans la suite on condidère le flacon nu qui est constitué de verre de conductivité thermique l = 1,3 W m-1 K-1.
4. Rappeler la loi de Fourier.
Le flux thermique à travers une surface simple est : F = lS (T2-T1) / e.
Flux en watt ; l conductivité thermique en W m-1 K-1; S : surface en m2 ; T2-T1 différence de température en K ; e : épaisseur de la paroi en m.
5. Donner l'expression de la résistance thermique de conduction.
R = e / (lS) exprimée en K W-1.
6. Soit C la
capacité calorifique de l'eau contenue dans le flacon ( on néglige
celle du verre). Etablir un bilan énergétique pour l'eau contenue dans
le flacon pendant un intervalle de temps dt pendant lequel sa
température varie de dT. On ne considère que le transfert thermique par
conduction à travers le flacon. On note Ta la température supposée constante de l'air extérieur.
Transfert thermique de conduction : lS (T-Ta) dt / e.
Energie perdue par l'eau : -C dT.
lS (T-Ta) dt / e.= -C dT.
7. Montrer que la température de l'eau vérifie l'équation différentielle : dT / dt + T / t = Ta / t où t est une constante de temps.
lS (T-Ta) dt / e = -C dT ; dT / dt = -lS (T-Ta) / (Ce).
On pose t = Ce / (lS) ; dT / dt = -T / t +Ta / t.
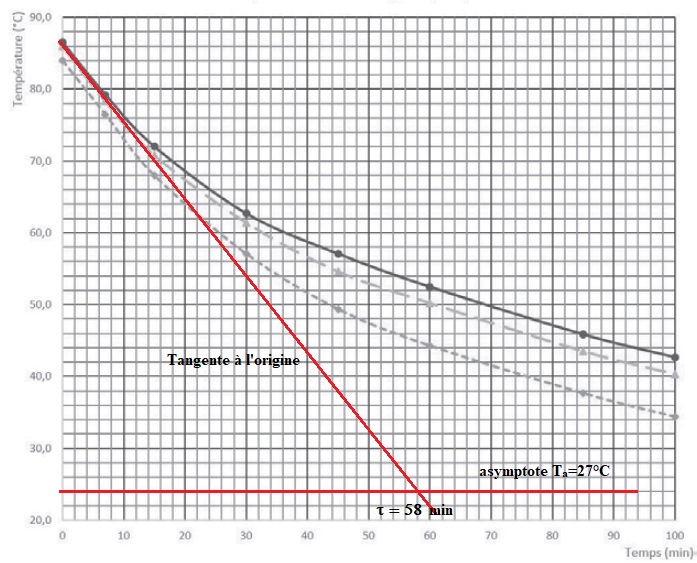
8. On donne la courbe obtenue pour le groupe 1 avec Ta = 27°C. Estimer la constante de temps.
|
...
|
....
|
Epaisseur de la combinaison.
On s'intéresse à la protection du corps du skieur en régime permanent
par une combinaison d'épaisseur e constituée de duvet de conductivité
thermique l = 0,04 W K-1 m-1. Ta = -10°C.
9. Identifier les trois modes de transfert énergétique.
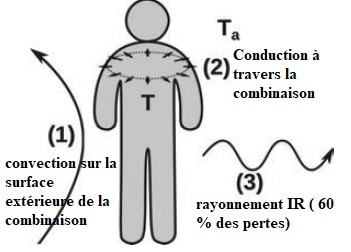
10. Légender le schéma électrique équivalent en indiquant les 9 grandeurs thermiques correspondant aux 9 éléments électriques.
Conduction à travers la combinaison : Pcd = (T-Tc) / Rcd.
Rcd : résistance thermique de la combinaison ; TC température sur la face extérieure de la combinaison.
Rayonnement sur la surface extérieure de la combinaison : Pr = (Tc-Ta) / Rr.
Rr = 1 / (aTa3S) avec a = 2,3 10-7 Wm-2 K-4.
Rr = 1 / (2,3 10-7x(263)3x1,3) = 0,184 K W-1.
Convection sur la face extérieure de la combinaison. Pcv = (Tc-Ta) / Rcv.
Rcv = 1 /(hS) avec h = 4,0 Wm-2 K-1. Surface S = 1,3 m2.
Rcv =1/(4,0 x1,3)=0,192 K W-1.
Ces pertes sont compensées par la production métabolique de puissance Pm = 150 W.

11. Déduire de ce schéma l'expression de la résistance thermique équivalente R telle que Pm =Pcd=(T-Ta) / R en fonction de Rr, Rcd et Rcv.
Résistance équivalente à Rr et Rcv en parallèle : Rr Rcv / (Rr+Rcv).
R = Rcd +Rr Rcv / (Rr+Rcv).
12. Exprimer l'épaisseur e en fonction de l, S, T, Ta, Pm, Rcv et Rr.
Calculer Pm, Rr, Rcd puis e pour que T = 37°C.
Rcd = e / (lS) ;
R =e / (lS) +Rr Rcv / (Rr+Rcv) ;
Pm =(T-Ta) / R ; R = (T-Ta) / Pm.
e / (lS) +Rr Rcv / (Rr+Rcv) = (T-Ta) / Pm.
e = [(T-Ta) / Pm - Rr Rcv / (Rr+Rcv)] lS.
Rr = 0,184 K W-1 ;
Rcv =0,192 K W-1. Pm = 150 W. T-Ta = 47 K.
e = [47 / 150 - 0,184 x 0,192 / (0,184+0,192)] x0,04 x1,3 =0,011 m = 1,1 cm.
|
|



