Isolation
et chauffage d'un logement. Concours
CAPLP
2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Transfert de chaleur.
1.1 Citer les noms des trois modes de transferts de la chaleur.
Conduction, convection et rayonnement.
1.2. Rappeler les valeurs limites de longueur d'onde du domaine des infrarouges ( IR).
780 nm à 1 mm.
1.3. Expliquer le principe de la thermographie infrarouge.
Une
caméra infrarouge permet de capter des rayonnements infrarouges et de
restituer les informations obtenues sous la forme d’une image visible.
Son principe repose sur le phénomène physique selon lequel chaque corps
dont la température est supérieure au zéro absolu émet un rayonnement
électromagnétique. Elle est utilisée pour effectuer la thermographie de
façade permettant de mettre en évidence les ponts thermiques et les
défauts d’isolation. En thermographie infrarouge, on travaille
généralement dans une bande spectrale qui s’étend de 2 à 15 μm.
1.4. Indiquer un exemple de partie du logement bien isolée, un exemple de partie mal isolée. Justifier.
Dans l’image ci-dessous, les parties les plus claires correspondent aux
zones où les pertes d’énergie sont maximales.
 Chauffage du séjour.
2.1. Soit F le flux de chaleur sortant de cette pièce. Soit DT la différence de température entre l'intérieur ( 19°C) et l'extérieur ( 0°C.
Chauffage du séjour.
2.1. Soit F le flux de chaleur sortant de cette pièce. Soit DT la différence de température entre l'intérieur ( 19°C) et l'extérieur ( 0°C.
Calculer F. Rg = 2,0 10-3 K W-1.
F = DT / Rg =19 / (2,0 10-3) =9,5 103 W = 9,5 kW.
2.2.
En déduire, sans calcul mais en justifiant, la puissance électrique
délivrée par les quatre convecteurs. Indiquer s'ils fonctionnent à
plein régime.
Puissance électrique délivrée = flux thermique = 9,5 kW.
4 convecteurs de puissance électrique 3,0 kW chacun.
4 x3,0 = 12 kW > 9,5 kW ; les convecteurs ne fonctionnent pas à plein régime.
2.3. Déterminer l'intensité efficace du courant circulant dans le circuit dédié au chauffage du séjour.
9,5 103 / 220 =43,18 ~43 A.
2.4. En déduire
l'intensité efficace du courant traversant chaque convecteur, supposé
purement résistif, en faisant une hypothèse sur leur fonctionnement.
Si les convecteurs montés en dérivation, sont réglés de la même manière : I = 43,18 / 4 = 10,8 ~11 A.
Modélisation du chauffage.
Le professeur souhaite proposer une activité expérimentale permettant
de modéliser le système de chauffage du séjour et de vérifier les
calculs précédents.
3.1. Indiquer les capacités et connaissances du programme abordées loors de cette activité.
Les dipôles ohmiques transforment intégralement l'énergie électrique en énergie thermique.
Savoir brancher un ampèremètre ( série) et un voltmètre ( en dérivation)
Connaître la relation Puissance = tension x intensité.
3.2.
Proposer une liste de matériel en indiquant les caractéristiques des
dipôles utilisés et les conditions expérimentales envisagées, notamment
au sein du générateur.
3.3. et 3.4 Présenter sous forme de schéma, le montage expérimental attendu en y intégrant les appareils de mesure.
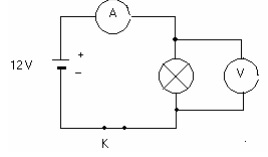
Réaliser le circuit ci-dessus.
Pour chaque lampe, relever la valeur de la tension U aux bornes de la lampe et l'intensité du courant qui la traverse.
Lire les inscriptions sur le culot des lampes.
Comparer le produit U x I pour chaque lampe à la valeur indiquée sur le culot.
Quelle grandeur représente ce produit et quelle est son unité ?
Isolation initiale du séjour.
4.1. Calculer la résistance thermique Rt équivalente des deux fenètres.
Epaisseur du verre : 5,0 mm ; Surface vitrée 0,91 m2 pour chaque fenètre. lverre = 1,00 W m-1 K-1.
Pour une fenètre : R = e / (lverreS) =5,0 10-3 /(1,00 x0,91) =5,5 10-3 W-1 K.
Pour deux fenètres : 1 / Rf = 1 / R + 1 /R = 2 / R ; Rf = 0,5 R =2,75 10-3 W-1 K.
4.2. Comparer la résistance thermique des fenètres à Rg, résistance thermique globale de la pièce.
Rg =2,0 10-3 K W-1. Rg est à peu près égale à Rf.
4.3. Montrer que 1 / Rg = 1 /Rm +1/Rf où Rm est la résistance thermique des murs, si on néglige les pertes d'énergie par le plancher, le plafond.
Flux thermique à travers les fenètres : DT / Rf.
Flux thermique à travers les murs : DT / Rm.
Flux thermique total : DT / Rg = DT / Rf +DT / Rm.
4.4 En déduire la valeur de Rm et conclure sur l'isolation prioritaire à entreprendre dans cette pièce.
1 /Rm =1 / Rg -1/Rf = 1000 (1 / 2 - 1 /2,75) =136,4 ; Rm =1 / 136,4 =7,3 10-3 K W-1.
Rm est environ trois fois plus grande que Rf. L'isolation prioriataire concerne le changement des fenètres.
4.5. Indiquer si l'hypothèse de pertes d'énergie négligées modifie cette conclusion.
L'hypothèse de pertes d'énergie négligées ne modifie pas cette conclusion.
Changement de fenètres.
Des double vitrages standard 4/16/4 ont été choisis. Les surfaces vitrées restent de dimensions identiques.
B.1.1 Montrer que la résistance thermique de fenètres augmentent avec un double vitrage. lair = 0,023 W m-1 K-1.
B1.2 Calculer la nouvelle réistance thermique R'f des nouvelles fenètres.
Pour une fenètre : R' = (everre / lverre + eair / lair) / S =(8 / 1,00 +16 /0,023) 10-3 / 0,91 =0,773 K W-1.
Pour deux fenètres : 1 / R'f = 1 / R' +1 / R' = 2 / R' ; R'f =0,773 / 2 =0,387 K W-1.
Choix du matériau d'isolation mural.
Le choix se porte sur une épaisseur de 40 mm de laine de roche ou de
polystyrène expansé. Ce matériau sera associé à une plaque de plâtre
d'épaisseur 10 mm.
B.2.1. A la question "Qu'est-ce qu'un bon isolant ? un élève répond " un isolant, ça garde la chaleur". Commenter.
Un bon isolant diminue les transfert thermiques par conduction ; il ne garde pas la chaleur.
Réaliser le montage expérimental ci-dessous permettant de mesurer
l'évolution de la température de l'air contenu dans les récipients non
isolé et isolés. Lancer lacquisition pendant 15 minutes avec
enregistrement d'une valeur de température toutes les 10 secondes.
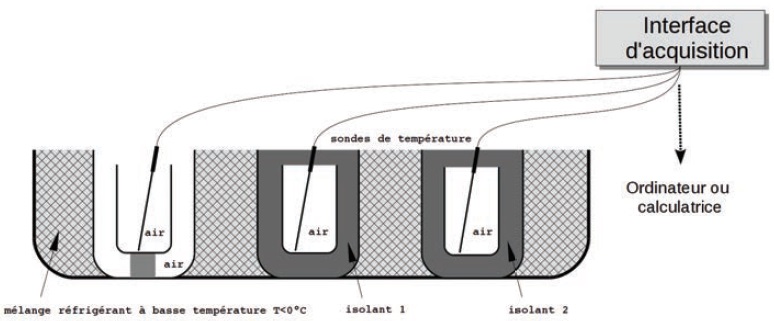
Isolant 1 : 40 mm laine de roche l =0,035 W m-1 K-1.
Isolant 2 : 40 mm polystyrène expansé l =0,045 W m-1 K-1.
B.2.2.Justifier le choix de l'Exao lors de cette activité expérimentale.
Précision sur la mesure du temps ; acquisition d'un grand nombre de mesures ; traitement des données.
B.2.3. Proposer un protocole détaillé pour réaliser le mélange réfrigérant.
Réaliser un mélange 2/3 glace pillée et gros sel ( 1 /3).
B.2.4 On appelle C ( J K-1) la capacité thermique globale du becher rempli d'air, R sa résistance thermique, Ti sa température initiale et Ta
la température du mélange réfrigérant. Démontrer que l'évolution de la
température du becher à l'instant t suit une décroissance exponentielle.
Flux de chaleur pendant la durée dt : dQ /dt= C dT / dt = (Ta- T) / R.
dT / dt +T / (RC) = Ta / (RC) (1).
Solution générale de dT / dt +T / (RC) =0 : T = Cste exp(-t / (RC) ).
Solution particulière de (1) : T = Ta.
Solution générale de (1) : T = Cste exp(-t / (RC) )+ Ta.
A l'instant initial : Ti = Cste + Ta ; Cste = Ti-TA.
T = (Ti-TA ) exp(-t / (RC) )+ Ta.
B.2.5. Vérifier dans cette expression la valeur de t à t = 0 et déterminer la valeur théorique de t pour obtenir T=Ta. Commenter cette valeur et donner une valeur caractéristique plus pratique.
T = (Ti-TA ) exp(0) )+ Ta = Ti-TA +Ta = Ti.
Si t tend vers l'infini, exp(-t / (RC) ) tend vers zéro et T tend vers TA.
Pratiquement, si t = 5 RC : exp(-5 ) = 0,0067 et T est très proche de TA.
B.2.6.
Indiquer ce qu'il faut modifier dans la formule du B.2.4 si le becher
est maintenant isolé. Montrer sans calcul, à partir de cette formule,
que le refroidissement sera ralenti.
Si le becher est isolé, sa résistance thermique croît : RC augmente et exp(-t / (RC) ) diminue.
B.2.7. Tracer l'allure de la courbe correspondante au bécher non isolé. Justifier.
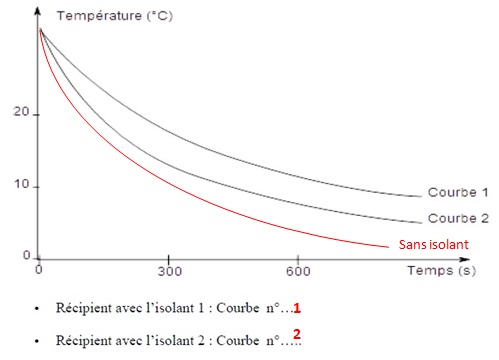
La température du becher décroît plus rapidement en absence d'isolant.
B.2.8. En déduire le matériau qu'il convient de choisir pour l'isolation du logement. Justifier.
La laine de roche est à retenir ; sa conductivité thermique est la plus
faible et en conséquence la résistance thermique est plus grande.
B.2.9. Une fois l'isolation terminée, la résistance thermique du séjour vaut R = 9 10-3 K W-1. déterminer la puissance des convecteurs pour maintenir la température à 19°C. Commenter.
Flux thermique : DT / R = 19 / (9 10-3) =2,1 103 W = 2,1 kW au lieu de 9,5 kW.
Les pertes thermique sont divisées par 4.
B.2.10. Expliquer l'expression " pont thermique".
Un pont thermique est une petite zone dans l'enveloppe d'un bâtiment,
possédant une résistance thermique plus faible. Dans cette zone, la
barrière isolante est rompue.
|
...
|
....
|
Une conséquence indirecte de l'isolation thermique : l'isolation acoustique.
Un
poids lourd a une émission sonore d'intensité maximale autour de 125
Hz,( L = 76 dB) une voiture autour de 1 000 Hz ( L = 70 dB).
B.3.1. Expliquer la différence entre son et bruit.
Les sons autres que la parole ou la musique s'assimilent souvent aux bruits.
On entend souvent des sons complexes comme la voix, constitués de
plusieurs sons purs. Lorsque le nombre de sons purs mélangés augmente,
devient plus complexe, il s'agit d'un bruit.
B.3.2. Donner la relation entre intensité sonore I( W m-2) et niveau d'intensité acoustique L en dB.
L = 10 log ( I / I0) avec I0 = 10-12 W m-2.
B.3.3. On suppose le croisement de deux camions devant la maison. Déterminer le niveau acoustique relevé.
Pour un camion seul : I = 10-12 x 107,6 =10-4,4 ~ 4 10-5 W m-2.
Pour deux camions : I = 8 10-5 W m-2.
L = 10 log(8 10-5 / 10-12) ~ 79 dB.
B.3.4. Même calcul lorsqu'un camion et une voiture se croisent.
Pour la voiture seule : I = 10-12 x 107 =10-5 W m-2.
Pour les deux véhicules : I =5 10-5 W m-2.
L = 10 log(5 10-5 / 10-12) ~ 77 dB.
B.3.5. En réalité les niveaux sonores dans la maison sont inférieurs à ces valeurs. Citer deux raisons à cette différence.
Les bruits se propagent dans toutes les directions.
Les murs et fenètres atténuent l'intensité acoustique.
B.3.6. Avant
changement des fenètres et avant isolation des murs, le niveau
d'intensié acoustique mesuré dans le séjour est en moyenne de 38 dB
pour des fréquence sonores de 800 Hz. Proposer une activité permettant
d'évaluer expérimentalement l'atténuation du niveau d'intensité
acoustique attendue après isolation.
Relier un générateur de fonction à un haut-parleur afin qu'il délivre
une tension de fréquence 400 Hz en régime sinusoïdal. Placer un
sonomètre à 10 cm devant le haut-parleur. Insérer des plaques de même
épaisseur mais de différents matériaux ente le sonomètre et le
haut-parleur.
Qualité de l'air intérieur dans la cuisine.
Température de l'air : 19°C ; volume de la pièce : 30 m3.
C.1.1. Rappeler les trois constituants principaux de l'air sec, en précisant leurs pourcentages et écrire leurs formules de Lewis.
Diazote (78 %), dioxygène ( 21 %), gaz nobles comme l'argon ( ~ 1 %).
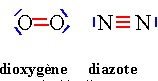
C.1.2 Ecrire les configurations électroniques des atomes rencontrés dans ces constituants.
N : 1s2 2s2 2p3 ; O : 1s2 2s2 2p4 ; Ar : 1s2 2s2 2p6 3s2 3p6.
C.1.3. En assimilant l'air sec à un gaz parfait, montrer que, à pression constante, sa masse volumique r est reliée à la température T par la relation r T = r0 T0, r0 et T0 étant les valeurs à 0°C.
PV = nRT ; P =nRT / V = n RT0 / V0 ; m / Mair T / V =m / MairT0 / V0 ; m / V T = m / V0 T0 ; r T = r0 T0.
C.1.4. En déduire la masse volumique de l'air sec à 19°C.
r = 1,29 x273 / 292 =1,206 ~1,21 kg m-3.
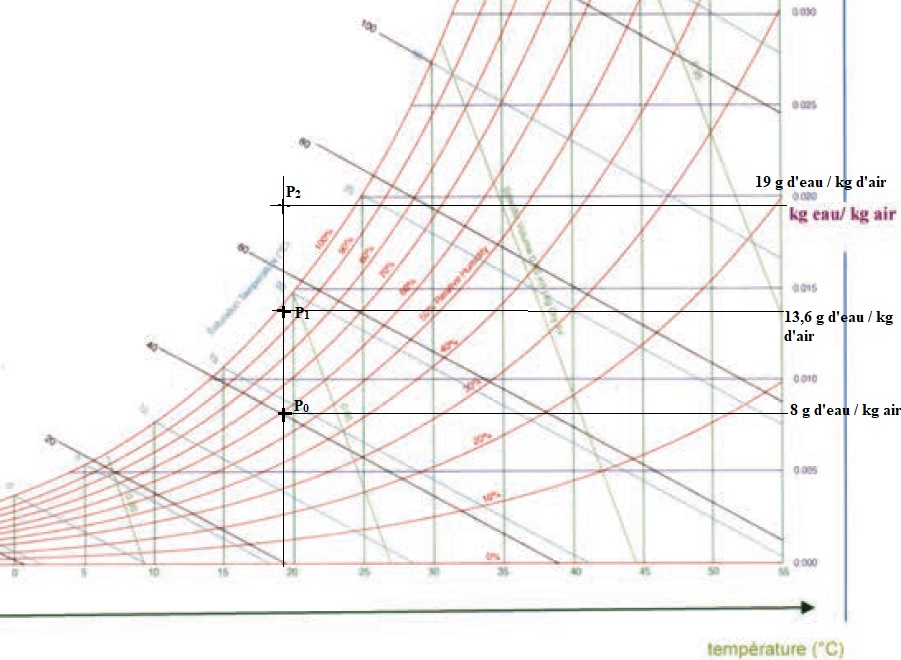
C.1.5. En supposant le taux d'humidité relative de 60 %, placer sur le diagramme, le point P0 correspondant.
C.1.6. Considérons qu'une cuisson génère 200 g de vapeur d'eau, déterminer la masse d'eau par m3 d'air ainsi rajoutée. Placer le point P1 sur le diagramme. Proposer une analyse du résultat en terme de confort.
Humidité absolue initiale 8 g d'eau par kg d'air ; 30 x1,21 =36,3 kg d'air dans la pièce.
36,3 x8 = 294,4 g d'eau dans la pièce.
Masse d'eau totale : 294,4 + 200 = 494,4 g d'eau dans 36,3 kg d'air soit 494,4 / 36,3 =13,6 g d'eau / kg d'air.
Développement de bactéries et de champignons.
C.1.7. La cuisson continuant, 200 g de vapeur d'eau supplémentaires sont dégagés. Placer le point P2 correspondant en commentant les phénomènes qui seront observés.
694,4 g d'eau dans 36,3 kg d'air soit 694,4 / 36,3 ~19 g d'eau / kg d'air.
Formation de goutelettes dans l'air ; condensation sur les parois plus froides.
Un moyen de résoudre ces problèmes est de renouveler régulièrement l'air en installant une VMC.
C.2.1. En appelant
d le débit de la VMC, S la surface du piquage, montrer que la vitesse
de l'air à l'entrée du piquage s'exprime par Vair = d / S.
d ( m3 /s) = Vair ( m / s) x S (m2).
C.2.2 Vérifier que Vair ~ 1 m /s pour le régime de petite vitesse (diamètre = 125 mm ; débit= 45 m3 /h) de la VMC.
S = 3,14 x 0,1252 / 4 =0,0123 m2 ; débit : 45 / 3600 =0,0125 m3 /s.
Vair =0,0125 / 0,0123 ~1,0 m /s.
C.2.3 Ecrire
l'équation de Bernoulli pour le cas de l'écoulement de l'air en
rappelant les conditions d'application de cette relation.
Pour un fluidehomogène, incompressible en régime perament soumis uniquement aux fores de pression et de pesanteur :
½r v2 +rgz + P = Cste.
C.2.4 Faire les simplifications dans celle-ci en supposant l'absence de
dénivelé entre la VMC et la bouche d'extraction et la quasi immobilité
de l'air dans la pièce, loin de l'embouchure.
Entre un point A situé au milieu de la pièce et un autre point B à la bouche d'extraction :
PA +rgzA= ½r v2B +PB +rgzB.
C.2.5. En déduire la dépression en Pa au niveau de l'embouchure.
PA -PB = ½r v2A +rg(zB-zA)= 0,5 x1,21 x 12 +1,29 x9,8x1,2= 15,77~ 16 Pa.
C.2.6. Un élève
approche une feuille de papier devant l'embouchure. La feuille reste
plaquée à l'embouchure. Faire un schéma en faisant le bilan des forces
qui s'exercent sur la feuille.
La feuille est soumise à son poids, verticale vers le bas et à une force verticale vers le haut due à la dépression.
C.2.7 Déterminer la masse maximale de la feuille qui pourra être plaquée à l'embouchure.
mg = (PA -PB ) x S avec S = 0,0123 m2 ;
m =15,77 x 0,0123 / 9,8 ~0,020 kg ( 20 g).
C.2.8. L'air rejeté
est remplacé par de l'air extérieur, provenant d'ouvertures dans les
huisseries et d'écarts sous les portes intérieures de la maison.
Déterminer la quantité d'énergie nécessaire pour porter 45 m3 d'air extérieur de 0°C à 19°C. Cair = 103 J kg-1 K-1.
masse d'air : 45 x1,29 ~58 kg
Q = m Cair DT =58 x103 x19 =1,14 105 J = 114 kJ à chaque heure.
Puissance correspondante : 1,14 105 / 3600~32 W.
C.2.9. Comparer cette énergie à celle du chauffage de la pièce et conclure sur les intérêts et limites de la VMC.
Puissance du chauffage de la pièce isolée : 2,1 kW.
32 / 2100 ~0,015 (1,5 %).
Avantage : combattre l'humidité et renouveler l'air vicié.
Inconvénients : augmentation de la facture de chauffage ; effet de courant d'air froid près des ouvertures dans les
huisseries et d'écarts sous les portes intérieures de la maison.
|
|