Mathématiques,
DNB Métropole 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1 (20 points)
Cette feuille de calcul présente les températures moyennes mensuelles à Tours en 2019.

1) D’après le tableau ci-dessus, quelle a été la température moyenne à Tours en novembre 2019 ?
8,9 °C.
2) Déterminer l’étendue de cette série.
22,6 - 4,4 =18,2 °C.
3) Quelle formule doit-on saisir en cellule N2 pour calculer la température moyenne annuelle ?
=MOYENNE(B2;M2)
4) Vérifier que la température moyenne annuelle est 13,1 °C.
(4,4 + 7,8 +9,6 +11,2 +13,4 +19,4 +22,6 +20,5 +17,9 +14,4 +8,2 +7,8) / 12 =13,1 °C.
5) La température moyenne annuelle à Tours en 2009 était de 11,9 °C.
Le pourcentage d’augmentation entre 2009 et 2019, arrondi à l’unité, est-il de : 7 % ; 10 % ou 13 % ? Justifier la réponse.
(13,1-11,9) / 11,9 ~0,10 ( 10 %).
Exercice 2 (20 points)
Le Futuroscope est un parc de loisirs situé dans la Vienne. L'année 2019 a enregistré 1,9 million de visiteurs.
1) Combien aurait-il fallu de visiteurs en plus en 2019 pour atteindre 2 millions de visiteurs ?
2-1,9 = 0,1 million = 100 000 visiteurs.
2) L'affirmation « Il y a eu environ 5 200 visiteurs par jour en 2019 » est-elle vraie ? Justifier la réponse.
L'affirmation est vraie : 1,9 106 / 365 ~5205 visiteurs / jour.
3) Un professeur
organise une sortie pédagogique au Futuroscope pour ses élèves de
troisième. Il veut répartir les 126 garçons et les 90 filles par
groupes. Il souhaite que chaque groupe comporte le même nombre de
filles et le même nombre de garçons.
a) Décomposer en produit de facteurs premiers les nombres 126 et 90.
126 = 2 x 32 x7.
90 = 2 x32x5.
b) Trouver tous les entiers qui divisent à la fois les nombres 126 et 90.
1 ; 2 ; 3 ; 6 ; 9 et 18.
c) En déduire le
plus grand nombre de groupes que le professeur pourra constituer.
Combien de filles et de garçons y aura-t-il alors dans chaque groupe ?
18 groupes contenant 126 /18 =7 garçons et 90/18 = 5 filles.
4) Deux élèves de
3ème, Marie et Adrien, se souviennent avoir vu en mathématiques que les
hauteurs inaccessibles pouvaient être déterminées avec l’ombre. Ils
souhaitent calculer la hauteur de la Gyrotour du Futuroscope.
Marie se place comme indiquée sur la figure ci-dessous, de telle sorte
que son ombre coïncide avec celle de la tour. Après avoir effectué
plusieurs mesures, Adrien effectue le schéma ci-dessous (le schéma
n’est pas à l’échelle), sur lequel les points A, E et B ainsi que les
points A, D et C sont alignés.
Calculer la hauteur BC de la Gyrotour.
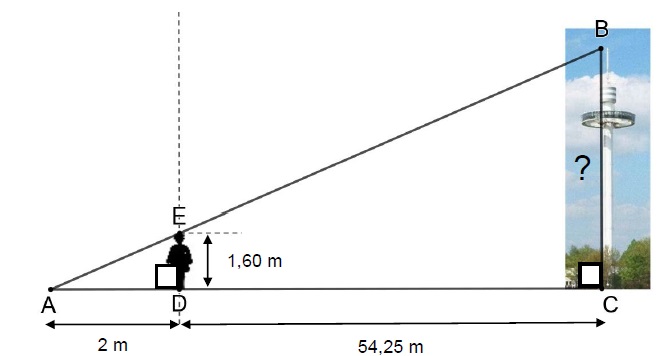
Propriété de Thalès :
AC / AD = BC / DE.
BC = AC x DE / AD = 56,25 x 1,6 / 2 =45 m.
Exercice 3 (20 points)
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n'est demandée.
Pour chaque question, trois réponses (A, B et C) sont proposées. Une
seule réponse est exacte. Recopier sur la copie le numéro de la
question et la réponse.
PARTIE A :
Une urne contient 7 jetons verts, 4 jetons rouges, 3 jetons bleus et 2
jetons jaunes. Les jetons sont indiscernables au toucher. On pioche un
jeton au hasard dans cette urne.
1. À quel événement correspond une probabilité de 7 /16 ?
A. Obtenir un jeton de couleur rouge ou jaune.
B. Obtenir un jeton qui n'est pas vert.
C. Obtenir un jeton vert. Vrai ( 7 jetons verts sur un total de 16 jetons)
2. Quelle est la probabilité de ne pas tirer un jeton bleu ?
13 /16 vrai ; 3 / 16 ; 3 /4.
13 jetons ne sont pas bleus sur un total de 16 jetons.
PARTIE B :
On considère la figure suivante, composée de vingt motifs numérotés de 1 à 20, dans laquelle :
- l'angle AOB mesure 36°.
le motif 11 est l’image du motif 1 par l’homothétie de centre O et de rapport 2.
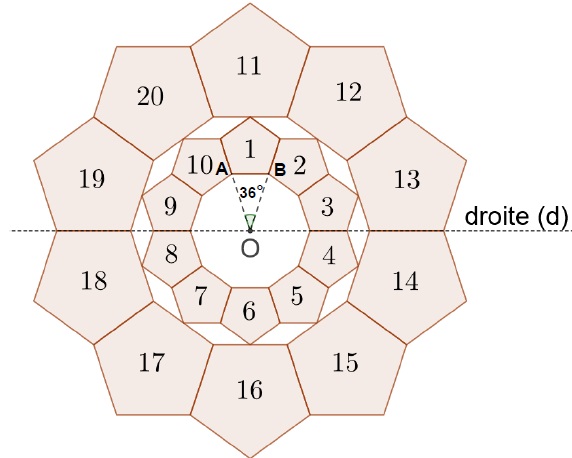
3. Quelle est l’image du motif 20 par la symétrie d’axe la droite (d) ?
motif 17 vrai ; motif 15 ; motif 12.
4. Par quelle rotation le motif 3 est-il l’image du motif 1 ?
Une rotation de centre O, et d’angle 36°.
Une rotation de centre O, et d’angle 72°. Vrai.
Une rotation de centre O, et d’angle 90°.
5. L’aire du motif 11 est-elle égale :
au double de l’aire du motif 1 ?
à 4 fois l’aire du motif 1. Vrai.
à la moitié de l’aire du motif 1.
|
|
....
|
Exercice 4 (20 points)
Voici un programme de calcul :
Choisir un nombre.
Prendre le carré du nombre de départ.
Ajouter le triple du nombre de départ.
Soustraire 10 au résultat.
1) Vérifier que si on choisit 4 comme nombre de départ, on obtient 18.
42+3x4-10=18.
2) Appliquer ce programme de calcul au nombre – 3.
(-3)2 + 3x(-3) -10 =9-9-10= -10.
3) Vous trouverez ci-dessous un script, écrit avec scratch.
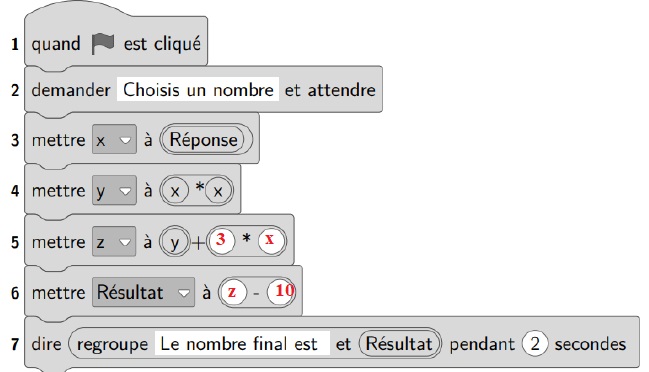
Compléter les lignes 5 et 6 pour que ce script corresponde au programme de calcul.
4) On veut déterminer le nombre à choisir au départ pour obtenir zéro comme résultat.
a) On appelle x le nombre de départ. Exprimer en fonction de x le résultat final.
x2+3x-10=0.
b) Vérifier que ce résultat peut aussi s’écrire sous la forme (x + 5)(x – 2).
On développe : (x+5)(x-2) = x2-2x+5x-10 =x2+3x-10=0.
c) Quel(s) nombre(s) doit-on choisir au départ pour obtenir le nombre 0 à l’arrivée ?
x+5 = 0 soit x = -5.
x-2 = 0 soit x = 2.
Exercice 5 (20 points)
La production annuelle de déchets par Français était de 5,2 tonnes par
habitant en 2007. Entre 2007 et 2017, elle a diminué de 6,5 %.
1) De combien de tonnes la production annuelle de déchets par Français en 2017 a-t-elle diminué par rapport à l’année 2007 ?
5,2 x 6,5 / 100 =0,338 t.
2) Pour continuer à diminuer leur production de déchets, de nombreuses familles utilisent désormais un composteur.
Une de ces familles a choisi le modèle ci-dessous, composé d’un pavé
droit et d’un prisme droit (la figure du composteur n’est pas à
l’échelle). Le descriptif indique qu'il a une contenance d’environ 0,5 m3. On souhaite vérifier cette information.
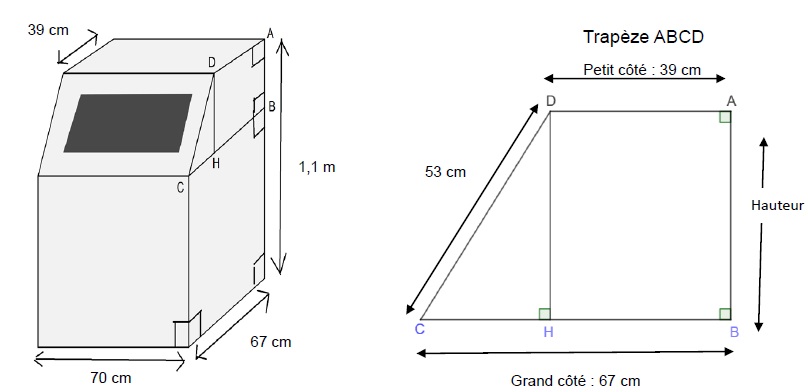
a) Dans le trapèze ABCD, calculer la longueur CH.
CH = BC-AD = 67 -39 = 28 cm.
b) Montrer que la longueur DH est égale à 45 cm.
DH2 = CD2-CH2 = 532-282=2025.
DH = 45 cm.
c) Vérifier que l'aire du trapèze ABCD est de 2 385 cm².
(AD + BC) x DH / 2 = (39 +67) x 45 /2 = 2 385 cm².
d) Calculer le volume du composteur.
(aire du trapèze ABCD + aire du rectangle situé sous le trapèze) x 70.
aire du rectangle situé sous le trapèze = 67 x(110-45)=4355 cm2.
(2385 +4355) x70 =471 800 cm3 =471,8 litres = 0,4718 m3.
L'affirmation « il a une contenance d’environ 0,5 m3 » est-elle vraie ? Justifier.
(0,5 -0,4718) / 0,5 = 0,058 ( 5,6 %).
A 5,6 % près l'affirmation est justifiée.
|
|