Mathématiques. Etudes graphiques.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
Les deux parties A et B sont indépendantes.
Partie A : absorption du principe actif d’unmédicament
Lorsqu’on absorbe un médicament, que ce soit par voie orale ou non, la
quantité de principe actif de ce médicament dans le sang évolue en
fonction du temps. Cette quantité semesure en milligrammes par litre de
sang.
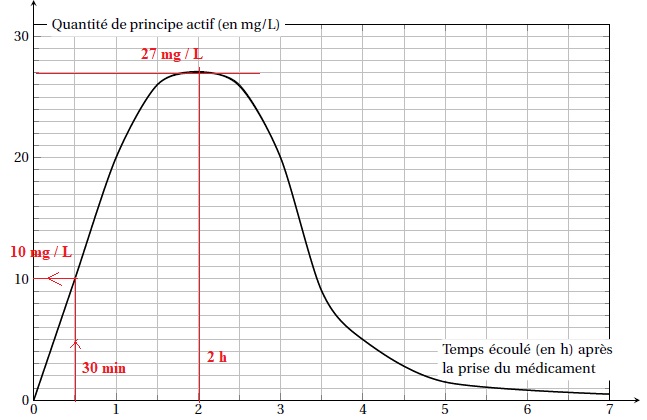
Le graphique ci-dessous représente la quantité de principe actif d’un
médicament dans le sang, en fonction du temps écoulé, depuis la prise
de ce médicament.
1. Quelle est la quantité de principe actif dans le sang, trente minutes après la prise de ce médicament ?
2. Combien de temps après la prise de ce médicament, la quantité de principe actif est-elle la plus élevée?
Partie B : comparaison de masses d’alcool dans deux boissons
On fournit les données suivantes :
Formule permettant de calculer la masse d’alcool en g dans une boisson alcoolisée : m =V ×d ×7,9
V : volume de la boisson alcoolisée en cL ; d : degré d’alcool de la boisson
(exemple, un degré d’alcool de 2% signifie que d est égal à 0,02)
Deux exemples de boissons alcoolisées :
Boisson 1 : Degré d’alcool : 5% ; Contenance : 33 cL.
Boisson 2 :Degré d’alcool : 12% ; Contenance 125 mL.
La boisson 1 contient-elle une masse d’alcool supérieure à celle de la boisson 2 ?
m1 = 33 x0,05 x7,9 ~13,0 g.
m2 = 12,5 x0,12 x7,9 ~11,80 g.
La boisson 1 contient une masse d’alcool supérieure à celle de la boisson 2.
Exercice 2.
Une
famille a effectué une randonnée en montagne. Le graphique ci-dessous
donne la distance parcourue en km en fonction du temps en heures.
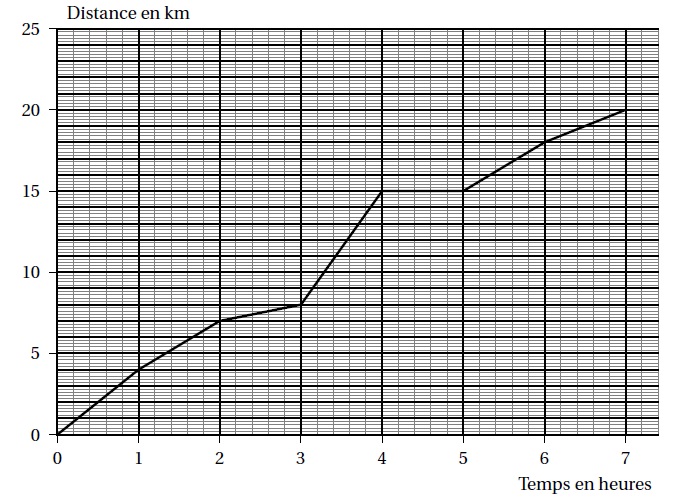
1. Ce graphique traduit-il une situation de proportionnalité? Justifier la réponse.
Non, le graphique n'est pas une droite passant par l'origine.
2. On utilisera le graphique pour répondre aux questions suivantes. Aucune justification n’est demandée.
a. Quelle est la durée totale de cette randonnée ? 7 heures.
b. Quelle distance cette famille a-t-elle parcourue au total ? 20 km.
c. Quelle est la distance parcourue au bout de 6 h demarche ? 18 km.
d. Au bout de combien de temps ont-ils parcouru les 8 premiers km ? 3 heures.
e. Que s’est-il passé entre la 4e et la 5e heure de randonnée ? Arrêt.
3. Un randonneur
expérimenté marche à une vitesse moyenne de 4 km/h sur toute la
randonnée. Cette famille est-elle expérimentée? Justifier la réponse.
6 heures de marche et 20 km parcourus ; vitesse moyenne : 20 / 6 = 10 /3 ~3,3 km / h.
La famille n'est pas expérimentée.
Exercice 3.
Le graphique ci-dessous donne les hauteurs d'eau au port de la Rochelle le 15/08/2018.
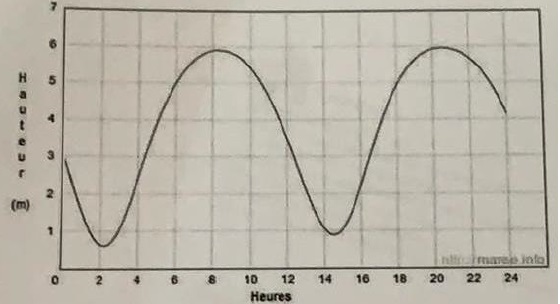
1. Quel a été le plus haut niveau ?
2. A quelles heures approximativement la hauteur d'eau a-t-elle été de 5 m ?
6 h ; 10h 20 ; 18 h ; 22 h35.
3.a Calculer le temps qui s'est écoulé entre la marée haute et la marée basse.
14 h30 -8 h16 = 6 h 14.
3.b. Calculer la différence de hauteur d'eau entre la marée haute et la marée basse.
5,89 -0,90 =4,99 m.
|
Heure
|
Hauteur (m)
|
Marée haute
|
8 h 16
|
5,89
|
Marée basse
|
14 h30
|
0,90
|
4. Comment qualifier la marée du 15 août 2018 entre 8 h16et 14 h30 à La Rochelle ?
Coefficient de marée = (Hhaut-Hbas) /5,34 x100 =4,99 / 5,34 x100 ~ 93.
Cette valeur étant supérieure à 70, la marée est qualifiée de vives-eaux.
|
Exercice 4.
Les activités humaines produisent du dioxyde de carbone (CO2)
qui contribue au réchauffement climatique.
Le graphique suivant représente l’évolution de la concentration
atmosphérique moyenne en CO2 (en ppm) en fonction du temps
(en année).
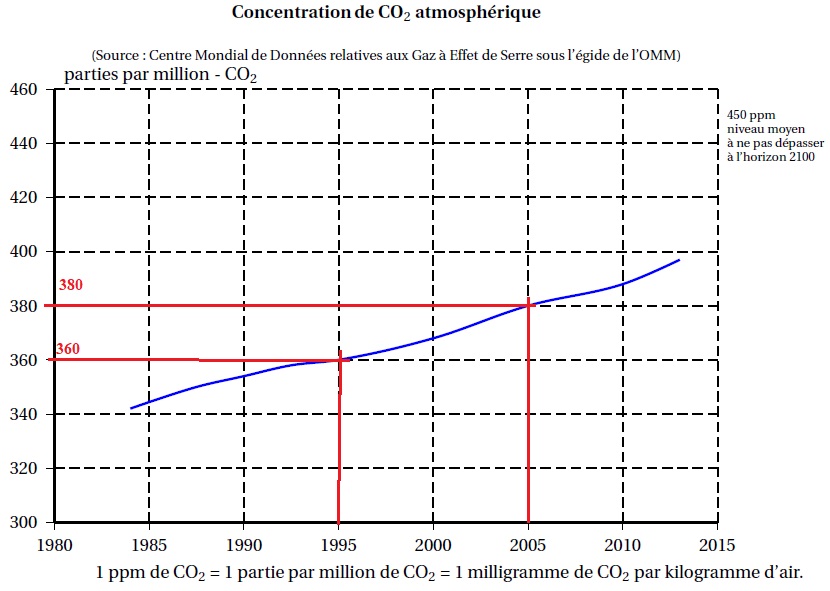
1. Déterminer
graphiquement la concentration de CO2 en ppm en 1995 puis en
2005.
2. On veut
modéliser l’évolution de la concentration de CO2 en fonction
du temps à l’aide d’une fonction g où g (x) est la concentration de CO2
en ppm en fonction de l’année x.
a.
Expliquer pourquoi une fonction affine semble appropriée pour modéliser
la concentration en CO2 en fonction du temps
entre 1995 et 2005.
Tous les points de la courbe bleue sont à
peu près alignés entre 1995 et 2005..
b.
Arnold et Billy proposent chacun une expression pour la fonction g :
Arnold propose l’expression g (x)= 2x −3630 ;
Billy propose l’expression g (x)= 2x −2000.
Quelle expression modélise le mieux
l’évolution de la concentration de CO2 ? Justifier.
2 x1995 -3630 =360 ; 2 x2005-3630 =380.
L’expression g (x)= 2x −3630 convient.
c. En
utilisant la fonction que vous avez choisie à la question précédente,
indiquer l’année pour laquelle la valeur de 450 ppm est atteinte.
450 = 2x-3630 ; 2x = 3630+450 =4080 ; x =
2040.
3. En France, les
forêts, grâce à la photosynthèse, captent environ 70 mégatonnes de CO2
par an, ce qui représente 15% des émissions nationales de carbone
(année 2016). Calculer une valeur approchée à une mégatonne près de la
masse M du CO2 émis en France en 2016.
70 / 0,15 ~ 467 mégatonnes.
Exercice 5.
Les représentations graphiques C1 et C2 de deux fonctions sont données dans le repère ci-dessous.
Une de ces deux fonctions est la fonction f définie par f (x) = −2x+8.
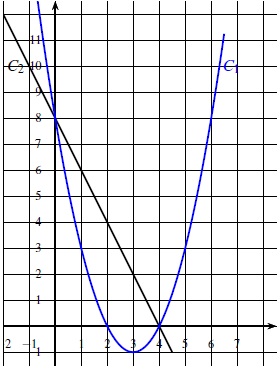
1. Laquelle de ces deux représentations est celle de la fonction f ?
Le graphe de la fonction affine f est une droite passant par les points de coordonnées (0 ; 8) et 4 ; 0) : donc C2.
2. Que vaut f (3) ?
f(3) = -2 x3 +8 = 2.
3. Calculer le nombre qui a pour image 6 par la fonction f .
6 = -2x +8 ; 2x = 8-6 = 2 ; x = 1.
4. La feuille de calcul ci -dessous permet de calculer des images par la fonction f .
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
x
|
-2
|
-1
|
0
|
1
|
2
|
3
|
2
|
f(x)
|
|
|
|
|
|
|
Quelle formule peut-on saisir dans la cellule B2 avant de l’étirer vers la droite jusqu’à la cellule G2 ?
= -2*B1+8
|
Exercice 6.
Chris fait une course de vélo tout terrain. le graphe ci-dessous
représente la fréquence cardiaque ( nombre de battements par minute) en
fonction du temps.
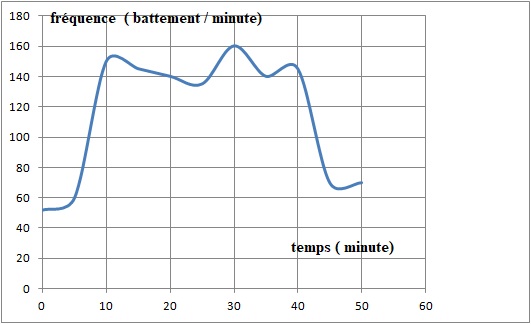
1. Quelle est la fréquence cardiaque de Chris au départ de la course ? ~ 52.
2. Quelle est la fréquence maximale atteinte au cours de la course ? 160.
3. Chris est parti à 9 H 33 de chez lui et termine sa course à 10 h 26. Quelle a été la durée en minutes de sa course ?
27 +26 = 53 minutes.
4. Chris a parcouru 11 km. Montrer que sa vitesse moyenne est d'environ 12,5 km /h.
11 / 53 x60 = 12,45 ~12,5 km / h.
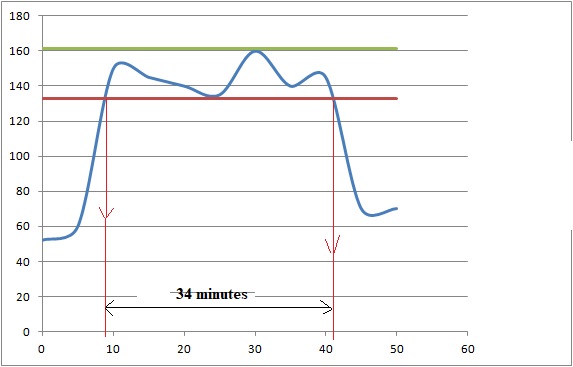
5. La fréquence
maximale ( FCM) de Chris est de 190 battements par minute.
L'effort est soutenu si la fréquence cardiaque mesurée est
comprise entre 70 et 85 % de la FCM.
Estimer la durée de la période pendant laquelle Chris a fourni un effort soutenu.
190 x0,70 = 133 ; 190 x0,85 = 161,5.
Exercice
7.
Les réponses aux questions de cet exercice seront lues sur la graphique suivant.
Celui-ci représente le profil d’une course à pied qui se déroule sur
l’île de la Réunion (ce graphique exprime l’altitude en fonction de la
distance parcourue par les coureurs), Aucune justification n’est
attendue pour les questions 1 à 4.
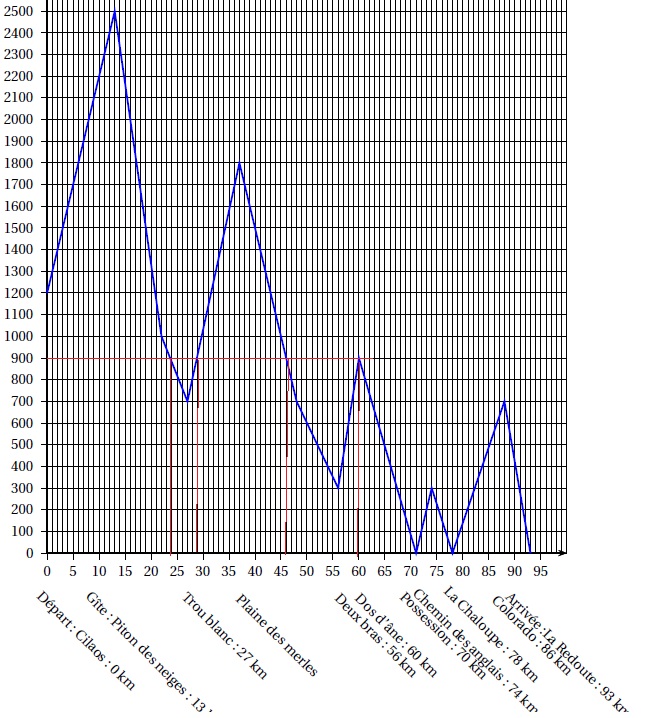
1. Quelle est la distance parcourue par un coureur, en kilomètres, lorsqu’il arrive au sommet de la plaine de 5 merles ?
37 km.
2. Quelle est l’altitude atteinte, en mètres, au gîte du Piton des neiges ?
2500 m
3. Quel est le nom du sommet situé à 900 mètres d’altitude ?
Dos d'âne.
4. À quelle(s) distance(s) du départ un coureur atteindra-t-il 1 900 m d’altitude?
7 et 18 km.
5. Le dénivelé
positif se calcule uniquement dans les montées ; pour chaque montée, il
est égal à la différence entre l’altitude la plus haute et l’altitude
la plus basse.
a. Calculer le dénivelé positif entre Cilaos et le gîte du Piton des neiges.
2500-1200 = 1300 m.
b. Montrer que le dénivelé positif total de cette course est 4 000 m.
1300 + (1800-700) + (900-300) +(300-0) +(700-0) = 4000 m.
6. Maëlle a effectué sa course à une vitesse moyenne de 7 km/h et Line a mis 13 h 20 min pour passer la ligne d’arrivée.
Laquelle de ces deux sportives est arrivée en premier ?
Durée de la course de Maélle : 93 / 7 ~13,29 h soit 13 h 17 min.
Maëlle est arrivée avant Line.
|







