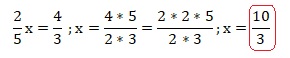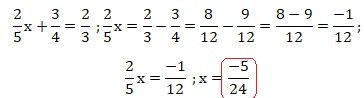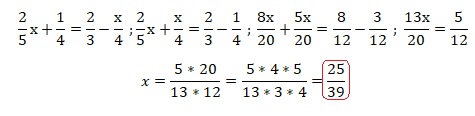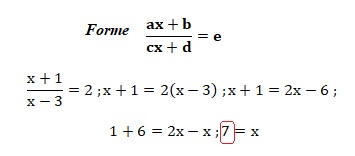Mathématiques.
Equation, inéquation.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Forme ax
= b.
4x =
-24.
x = -24 / 4 ; solution : x = -6.
3 x =0 ; solution : x =0.
0,5 x = -2 ;
x = -2 / 0,5 ; solution x = -4.
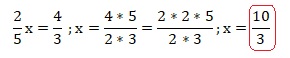
Forme ax +b = c.
3x-5 = 2.
3x = 2+5.
3x = 7 ; solution x = 7 /3.
-7x+3=6.
-7x = 6-3.
-7x = 3. Solution : x = -3 / 7.
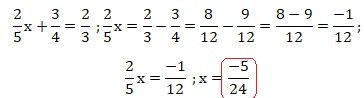
Forme ax+b = cx +d.
3x-1 = 7x -5.
-1 +5 = 7x -3x.
4 = 4x ; solution x = 1.
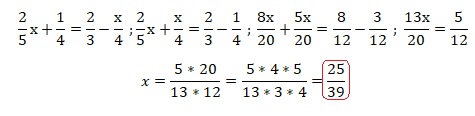
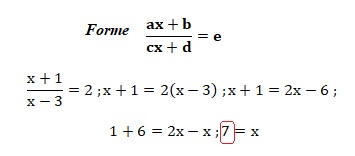
|
Inéquations.
Résoudre dans R
les inéquations suivantes :
x-3 < 0.
x < 3 soit ]-oo ; 3 ].
3x-2 < 3-2x.
3x +2x < 3 +2.
5x < 5 ; x < 1. Soit ]-oo
; 1 [
2(x-3) > 7-3x.
2x-6 > 7-3x.
2x+3x >7+6.
5x > 13 ; x > 13 /5 soit ]13 /5
; +oo[.
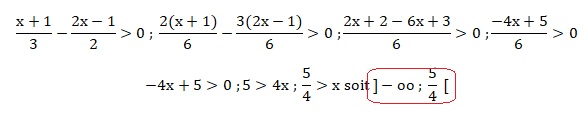
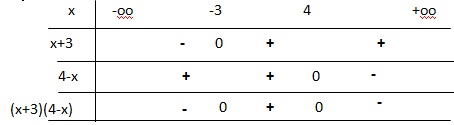
Déterminer, à l'aide d'un tableau, le signe des expressions suivantes :
(4-x) ( x+3).
|
Résoudre
dans R les inéquations.
(x2-9) (x+1) < 0.
On étudie le signe de (x+3)(x-3)(x+1).
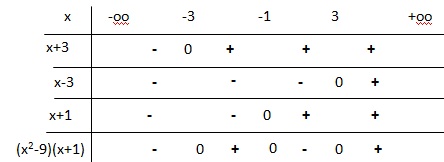
Solutions : ]-oo ; -3[ union ]-1 ; 3[.
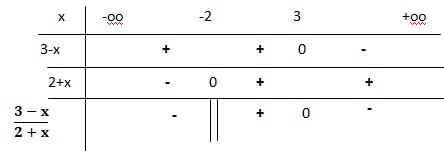
(5-2x) /(x2-1)
> 0.
Le dénominateur ne peut pas être nul.
x2-1 différent de zéro soit x différent de ±1.
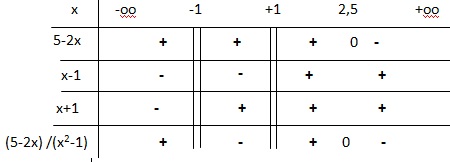
Solutions : ]-oo ; -1[ union ]1 ; 2,5 ].
Mise en équation d'un problème.
1. Rémy
dispose de 96 m de grillage avec lesquels il souhaite construire un
enclos pour son poney. Il cherche quelle forme donner à son enclos pour
que celui-ci ait la plus grande surface possible.
a. Sa première idée est de réaliser
un rectangle avec les 96 m de grillage.
Calculer
la longueur et la largeur de ce rectangle sachant que :
-
la longueur est le double de la largeur.
-
son périmètre est 96 m.
On note x la longueur : la largeur est égale à 0,5 x.
Périmètre : 2(x +0,5 x) = 96 ; x+0,5 x = 48 ; 1,5 x = 48 ; x = 48 / 1,5
=32 m.
Longueur : 32 m ; largeur : 32 / 2 = 16 m ; aire du rectangle : 32 x16
~512 m2.
b. Sa deuxième idée est de réaliser
un carré. Calculer l’aire d’un carré de 96 m de périmètre.
Côté
du carré : 96 / 4 = 24 m ; aire du carré : 24 x24 = 576
m2.
c. Sa troisième idée est de réaliser
un cercle. Calculer l’aire du cercle de 96 m de circonférence.
On
note R le rayon du cercle : R = 96 / (2p)~15,28 m.
Aire du disque : pR2
= 3,14 x15,282 ~733 m2.
2. Un enfant a ramassé 20
coquillages. Les grands mesurent 2 cm de long, les petits mesurent 1 cm.
Tous les coquillages mis bout à bout font 32 cm au total.
Combien a-t-il de grands
coquillages et combien de petits ?
On note x le nombre de
petits coquillages et 20-x le nombre de grands coquillages.
Longueur = 32 = x+2(20-x) ; 32 = x+40-2x ; x =8.
8 petits coquillages et 12 grands coquillages.
3. À l’entrée du parc d’ani-math-ion
figurent les informations suivantes :
Entrée adulte : 12 € Ouvert de 9 h à 18 h
Entrée enfant : 7 €. Dernières entrées à 17 h
Forfait famille (sur présentation du livret de famille) : 35 € Fermé le
lundi.
a. À partir de
quel nombre d’enfants, un couple a-t-il intérêt à choisir le forfait
famille ?
On note x le nombre d'enfants. 2 *12 + 7 x >35 ; 7x >35-24 ; 7x
>11 ; x > 11 / 7 ; x > 2.
b. Au
cours de cette même journée, 380 personnes n’ont pas utilisé le forfait
famille pour une recette correspondante de 3 660 €. Déterminer le
nombre d’entrées adultes et le nombre d’entrées enfants vendues lors de
cette journée.
On note x le nombre d'enfants ; nombre d'adultes : 380-x ;
(380-x) *12 + 7 x = 3660 ; 4560 -12x + 7x =3660 ;
4560 -3660 = 5x ; 900 = 5 x ; x = 900 / 5 = 180 enfants et 200 adultes.
4. Au goûter, Lise mange 1 / 4 du
paquet de gâteaux qu’elle vient d’ouvrir.
De
retour du collège, sa soeur Agathe mange les 2 / 3 des gâteaux restants
dans le paquet entamé par Lise. IL reste alors 5 gâteaux.
Quel était le nombre initial de gâteaux dans le paquet ?
On note x le nombre
de gateau.
Lise en mange : x / 4 = 0,25 x ; il en reste 0,75 x.
Agathe mange : 0,75 x * 2 /3 = 0,5 x ; il en reste 0,25 x = 5 soit x =5
/ 0,25 = 20.
|
.
|
|