Panne d'un drone en plein vol, bouilloire électrique, niveau d'intensité sonore, spécialité SI 2021.

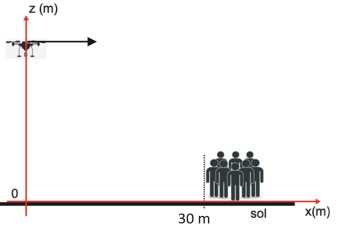
Panne d'un drone en plein vol.
Un drone est en mouvement rectiligne uniforme à la vitesse v₀, à l'altitude h = 100 m.
A l'instant t =0, les moteurs s'arrêtent alors que le drone vole en direction du public. Le drone est en chute libre.

1. Définir le modèle de la chute libre.
Le drone n'est soumis qu'à son poids.
2. Etablir la direction et le sens du vecteur accélération du drone au cours de sa chute.
La seconde loi de Newton donne : accélération verticale, vers le bas, valeur g = 9,81 m s^-2.
3. Etablir les équations horaires du mouvement du drone lors de sa chute.
Coordonnées du vecteur accélération : 0 ; -g.
Le vecteur vitesse est une primitive du vecteur accélération.
Coordonnées du vecteur vitesse initiale : v₀ , 0.
Coordonnées du vecteur vitesse : v₀ ; -gt.
Le vecteur position est une primitive du vecteur vitesse.
Coordonnées de la position initiale : 0 ; h = 100 m.
x = v₀ t ; z = -½gt² +100.
4. Montrer que l'abscisse du point d'impact au sol est x_P = v₀(2h /g)^½. Calculer sa valeur et commenter.
t = x_p / v₀ ; repport dans z :
z = 0 = -½g x_P² / v₀² +h.
x_P² = v₀² 2h / g.
x_P = v₀(2h /g)^½ avec v₀ = 3,00 m /s.
x_P = 3,00 (200 / 9,81)^½ =13,5 m, le public n'est pas touché.
5. Déterminer l'altitude minimale au-delà de laquelle le drone pourrait atteindre le public placé à 30 m à t = 0.
x_P² = v₀² 2h / g.
h = x_P² g / (2v₀² ) = 30² x9,81 / (2x9)=490 m.
A cette altitude, le drone est quasiment invisible ( il n'y a pas de spectacle pour le public).
On cherche à étudier la vitesse de chute.
6. Donner l'expression de la vitesse v_P au moment de l'impact.
Théorème de l'énergie cinétique entre les instants où les moteurs s'arrêtent et le moment où il touche le sol.
½mv_P² -½mv₀² = mgh.
v_P² -v₀² = 2gh.
v_P = (v₀² + 2gh)^½.

7. Associer chaque courbe au type d'énergie.

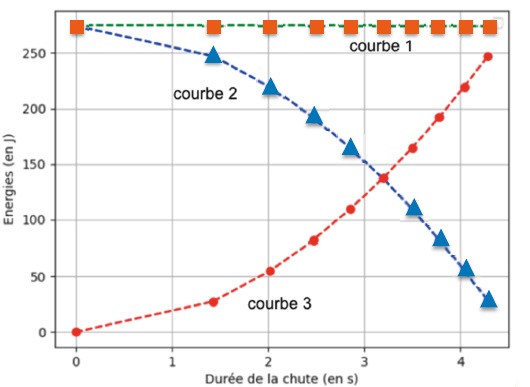
Courbe 1 : en chute libre, l'énergie mécanique est constante.
Courbe 2 : l'énergie potentielle de pesanteur diminue au cours de la chute.
Courbe 3 : l'énergie cinétique croît au cours de la chute.
8. Déterminer le phénomène qui n'a pas été pris en compte pour ces simulations.
Les frottements.
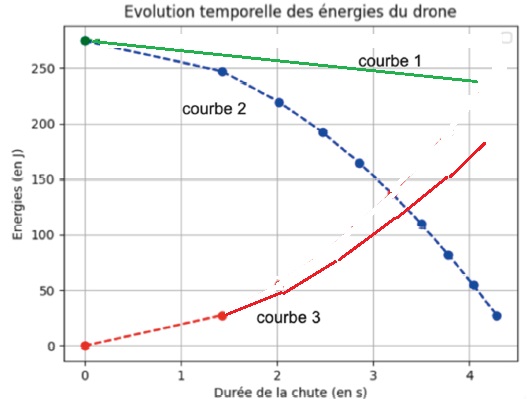
9. Dans le cas réel tracer la courbe modifiée représentant l'évolution de l'énergie mécanique en fonction du temps. Même question pour la courbe représentant l'énergie cinétique.
L'énergie mécanique diminue du travail des frottements.

Analye énergétique d'une bouilloire.
Le but de cet exercice est d'étudier les pertes d'énergie lorsque l'appareil porte à ébullition une certaine mase d'eau.
On met à chaufer dans la bouilloire 1,0 litre d'eau. On obtient le graphe suivant :

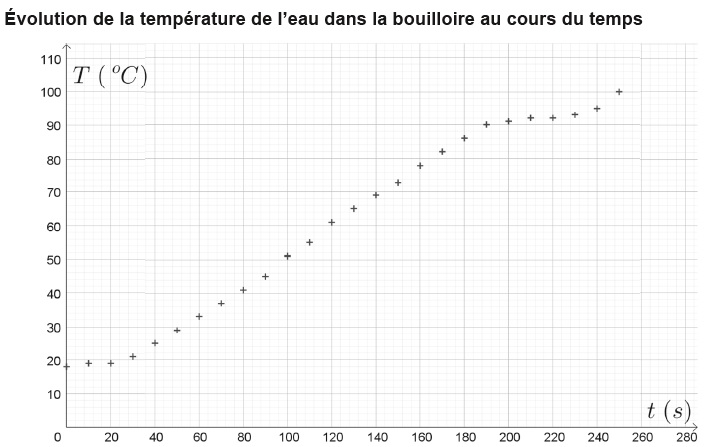
1. Déterminer la variation d'énergie interne de l'eau lorsque la température passe de T₁ = 20°C à T₂ = 90°C.
DU_eau = m C_eau ( T₂-T₁) =1 x4,18 10³ (90-20) =2,926 10⁵ ~2,9 10⁵ J.
2. Déterminer la valeur de l'énergie électrique reçue par la résistance électrique de la bouilloire pendant la durée de chauhhe de t₁ = 30 s à t₂ = 190 s.
Puissance électrique P = 2,0 kW.
E =P(t₂-t₁) = 2,0 10³(190-30)=3,2 10⁵ J.
Le vase de la bouilloire est en acier inoxydable ( C_vase = 3,0 10² J K^-1). On suppose qu'à chaque instant la température du vase reste égale à celle de l'eau.
3. Déterminer la variation d'énergie interne du vase lorsque la température passe de T₁ = 20°C à T₂ = 90°C. Commenter.
DU_vase = C_vase ( T₂-T₁) =3,0 10² (90-20) =2,1 10⁴ J.
DU_eau + DU_vase ~ énergie reçue par la résistance.
4. En supposant que toute l'énergie thermique cédée par la résistance est transférée à l'eau, déterminer la durée nécessaire pour augmenter la température de l'eau de 20°C à 90°C.
Energie reçue par l'eau / Puissance de la bouilloire =2,926 10⁵ / 2000= 146 ~1,5 10² s.
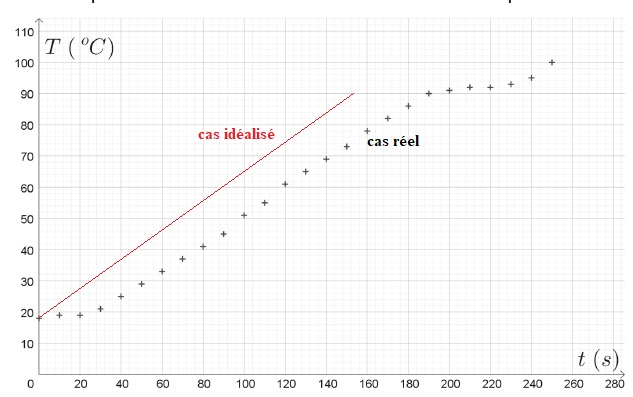
Représenter l'allure de l'évolution de la température de l'eau dans ce cas idéalisé.