Diffraction,
interf�rences : quelle taille pour les mailles d'un tamis ?
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
|
On utilise des tamis calibr�s pour s�lectionner les art�mies, crustac�s �lev�s pour nourrir les poissons.
1. V�rification de la longueur d'onde de la diode laser utilis�e.
On r�alise l'exp�rience suivante.
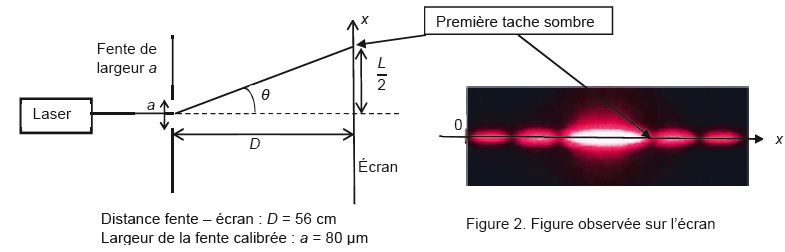
1.1- Nommer le ph�nom�ne physique responsable des taches lumineuses observ�es sur l'�cran.
La diffraction est d'autant plus marqu�e que la largeur de la fente est
plus proche de la longueur d'onde de la lumi�re utilis�e.
1.2- D�terminer l'expression de l'angle q en fonction de L et de D. En d�duire l'expression de l en fonction de L, a et D.
tan q = �L / D ~q pour les petits angles.
De plus q = l / a ; l = aL / (2D).
Pour une mesure plus pr�cise, on remplace l'�cran par une cam�ra qui
permet d'obtenir l'intensit� lumineuse relative( intensit� lumineuse
re�ue par le capteur / intensit� maximale re�ue ) en fonction de la
position x.
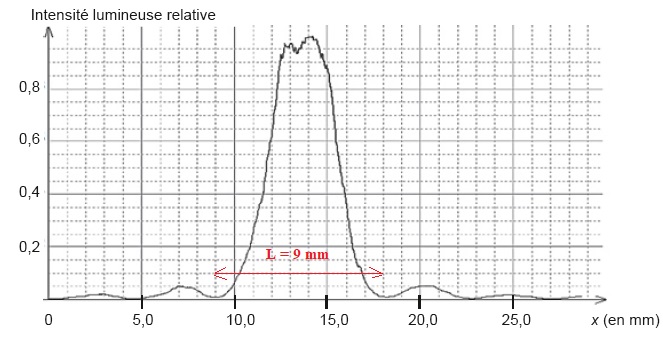
1.3- D�terminer la valeur de la longueur d'onde de la diode laser utilis�e.
l = aL / (2D) ; a = 8,0 10-5 m ; D = 0,56 m ; L = 9,0 mm = 9,0 10-3 m.
l =8,0 10-5 x9,0 10-3 / 1,12 =6,43 10-7 m = 643 nm.
Cette valeur est en accord avec la valeur (650 �10) nm annonc�e.
|
Calibrage du tamis.
On
veut v�rifier que le tamis permet de r�cup�rer toutes les art�mies
d'une taille sup�rieure � 150 �m. La largeur du fil plastique
constituant le tamis est �gale � 230 �m. On r�alise une exp�rience
d'interf�rences pour �valuer les dimensions du tamis.
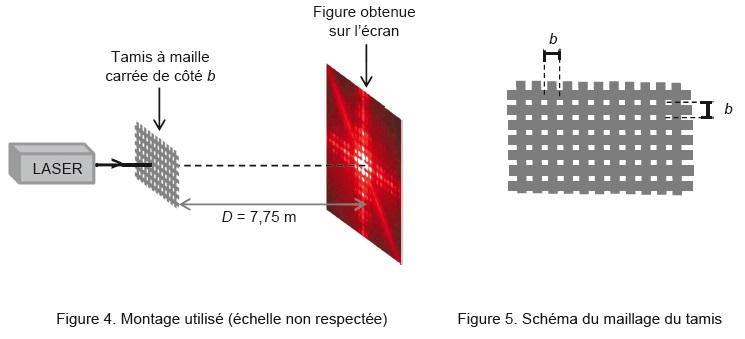
D = (7,75 �0,03) m
On obtient la figure d'interf�rences suivante.
2.1-
Expliquer sans calcul, l'origine de la pr�sence de zones sombres
et de zones brillantes dans une figure d'interf�rences lumineuses.
On observe un ph�nom�ne d ’interf�rences lumineuses en tout point d ’un �cran o� se superposent les 2 faisceaux lumineux issus des 2 sources secondaires S1 et S2.
Les interf�rences ne peuvent avoir lieu qu'entre deux ondes coh�rentes.
Dans la r�gion o� se superposent les ondes, l'intensit� lumineuse passe
par des maximums et des minimums qui peuvent �tre nuls. Les maximums
d�passent la somme des intensit�s des faisceaux pris s�par�ment.
Si
l'ordre d'interf�rence est un entier ( la diff�rence de marche est un
multiple de la longueur d'onde), les interf�rences sont constructives (
franges brillantes : �clairement maximal).
Si
l'ordre d'interf�rence est �gal � 2n+1 ( n entier) ( la diff�rence de
marche est un multiple impair de la demi longueur d'onde), les
interf�rences sont destructives ( franges noires).
L'interfrange not� i est d�fini comme la distance entre les centres de
deux taches lumineuses successives selon l'axe identifi� figure 7.
i = l D / b.
2.2- Evaluer la valeur de i ainsi que l'incertitude -type u(i).
i = 1,5 cm ; u(i) =0,25 mm.
2.3. Calculer b et �valuer u(b).
i = l D / b ; b = l D / i = 650 10-9 x 7,75 / (1,5 10-2)=3,36 10-4 m=336 �m.
u(b) / b =[(u(D) / D)2 +(u(i) / i)2 +(u(l) / l)2 ]�.
u(b) / b =[(0,03) / 7,75)2 +(0,25 / 15)2 +(10 /650)2 ]�~0,023.
u(b) =0,023 x336~8 �m.
b = (336 �8) �m.
2.4. Indiquer si le tamis �tudi� permet de r�cup�rer les art�mies voulues. Justifier.
Dimension des trous carr� du tamis : b-�paisseur du fil ;
valeur maximale := 336+8 -230=114 �m.
valeur minimale := 336-8 -230=98 �m.
Ces valeurs �tant inf�rieures � 150 �m, le tamis permet de r�cup�rer les art�mies voulues.
|
|
