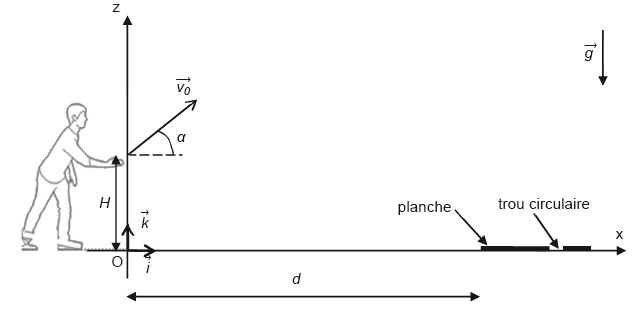
Le jeu du cornhole. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. Un joueur se place à une distance d de la planche afin de lancer son sac de maïs. Etude énergétique. Le mouvement du sac est filmé puis étudié à l'aide d'un logiciel de pointage. Extrait du programme écrit en langage python. 1-  Identifier les grandeurs calculées aux lignes 15, 16, 17 et 18. Ligne 15 : vitesse. Ligne 16 : énergie cinétique. Ligne 17 : énergie potentielle de pesanteur. Ligne 18 : énergie mécanique. 2- En justifiant le choix, attribuer à chaque série l'énergie qui lui correspond. 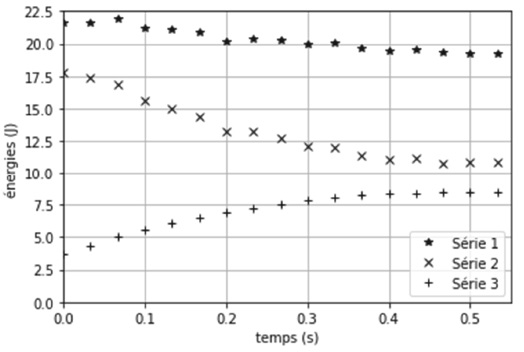Série 1 : énergie mécanique, somme des séries 3 et 2. Série 2 : l'énergie cinétique diminue du fait des frottements. Série 3 : énergie potentielle de pesanteur, l'altitude du sac croît dans la première phase du lancer. 3- Expliquer en quoi ces résultats permettent de considérer que l'action de l'air sur le sac n'est pas négligeable devant le poids du sac. L'énergie mécanique n'est pas constante, elle diminue du travail des frottements sur l'air. 4. Estimer la valeur de la vitesse initiale v0. Energie cinétique initiale : ~17,6 J ; masse du sac m =0,44 kg ; v0 = (2 Ec / m)½ =(2 x17,6 / 0,44)½ =8,94 ~8,9 m /s. 5- Estimer la valeur de l'altitude initiale H et commenter. Energie potentielle initiale : ~3,7 J ; H = Ep /(mg) = 3,8 /(0,44 x9,81) =0,88 m. Etude du mouvement du sac après le lancer. Les frottements de seront pas pris en compte dans cette partie. On donne les dimensions de la planche. 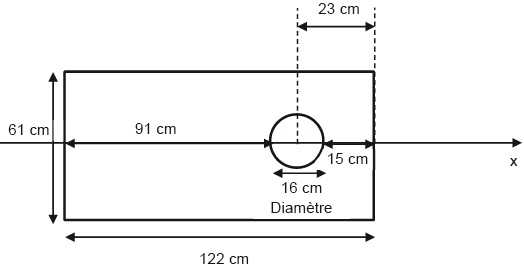1- Déterminer les expressions littérales des coordonnées du vecteur accélération. Le sac n'est soumis qu'à son poids. La seconde loi de Newton conduit à : ax = 0 ; az= -g. 2- En déduire les équations horaire x(t) et z(t). Le vecteur vitesse est une primitive du vecteur accélération et v0( v0 cos a ; v0 sin a). vx = v0 cos a ; vy = -gt +v0 sin a. Le vecteur position est une primitive du vecteur vitesse et la position initiale est (0 ; H). x(t) = v0 cos a t ; z(t) = -½gt2 + v0 sin a t + H.. 3- Montrer que l'équation horaire de la trajectoire est : z(x) = -½g x2 / (v0 cos a)2+ x tan a + H. t = x / (v0 cos a) ; repport dans z(t). z(x) = -½gx2 / (v0 cos a)2 + v0 sin a x / (v0 cos a) + H. z(x) = -½g x2 / (v0 cos a)2+ x tan a + H. Branche de parabole. 4- Indiquer les paramètres initiaux du lancement sur lesquels le joueur peut avoir une influence et qui jouent un rôle pour la réussite d'un lancer à trois points ( le sacpasse dans le trou circulaire) . Portée : z(x) =0 = -½g x2 / (v0 cos a)2+ x tan a + H. La portée dépend de la vitesse initiale, de l'angle a, et de H. Premier lancer : z(x) = -0,0842x2 +0,625 x +0,800. 5- Quel est le nombre de point(s) marqué(s) ? -0,0842x2 +0,625 x +0,800 =0. Discriminant : D = 0,6252 +4*0,8*0,0842 =0,66=0,8122 ; solution retenue : x=(-0,625 -0,812) / (-2*0,0842) =8,53 m. Le sac tombe sur la planche : 1 point. 6. Second lancer : même angle de tir, même hauteur H, vitesse initiale différente. Le sac tombe dans le trou. Déterminer la vitesse initiale. x=8,00 +0,91 +0,08 =8,99 m. Premier lancer : tan a =  0,625 ; a =32 ° ; cos a = 0,848. Second lancer : 0 =-½g x' 2 / (v'0 cos a)2+ x' tan a + H avec x' = 8,99. -½g x' 2 / cos2 a =-0,5 x9,81 x8,992/ 0,8482 = -551,27 ; x' tan a + H =8,99 x0,625 +0,800 =6,42. -551,27 / v'20 +6,42 = 0 ; v'20 =551,27 / 6,42 =85,87 ; v'0 =9,27 m /s ou 33,4 km /h.

menu