Les accélérateurs montent en puissance, bac S polynésie 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Etude simplifiée d'un accélérateur de protons.   Un proton de charge q=e et de masse m pénètre dans un accélérateur linéaire de particules. A t = 0, le proton est situé en O et possède une vitesse initiale de valeur v0 = 2,0 103 m /s et de direction Ox. Entre les armatures A et B séparées d'une distance l =6,5 cm règne un champ électrostatique uniforme E =10,0 kV / m. On néglige le poids devant la force électrique. 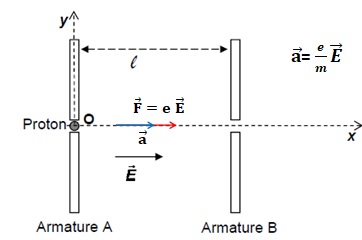1.1.  Représenter sans souci d'échelle, la force électrique F appliquée au proton ainsi que le vecteur accélération a de celui-ci.. 1.2. Vitesse et énergie du proton. 1.2.1.a. Montrer que vx(t) s'écrit : eE / m t + v0. Le vecteur vitesse est une primitive du vecteur accélération. vx(t) = eE / m t + constante. A t= 0, la vitesse vaut v0 ; vx(t) = eE / m t + v0. 1.2.1.b  Déterminer l'équation horaire vy(t) et justifier le nom d'accélérateur linéaire. Le poids étant négligeable devant la force électrique, la composante ay de l'accélération est nulle. La vitesse initiale étant horizontale, vy(t) = 0. Le mouvement du proton s'effectue suivant l'axe Ox ; le proton est accéléré, d'où le nom accélérateur linéaire. 1.2.2. Le proton atteint B à t1 = 3,7 10-7 s. Quelle est alors sa vitesse v1 ? m=1,7 10-27 kg ; e = 1,6 10-19 C. v1 = 1,6 10-19 x1,00 104 /( 1,7 10-27) x3,7 10-7 +2,0 103 =3,5 105 m /s. 1.2.3. Déterminer l'équation du second degré qui permet d'obtenir t1. Retrouver la valeur de t1. La position est une primitive de la vitesse ; le proton est initialement à l'origine O de l'axe Ox. x(t) = ½ at2 +v0t ; x(t) = ½e E / m t2 +v0t. x(t) =0,5 x1,6 10-19 x1,00 104 /(1,7 10-27)t2 + 2,0 103 t. x(t) =4,7 1011 t2 + 2,0 103 t. Au point B : 6,5 10-2 =4,7 1011 t12 + 2,0 103 t1. 4,7 1011 t12 + 2,0 103 t1 -6,5 10-2 = 0. Discriminant D = (2,0 103)2+4 x4,7 1011 x6,5 10-2 =1,2236 1011 ~(3,498 105)2. t1 = (-2,0 103 +3,498 105) / (2 x4,7 1011) ~3,7 10-7 s. 1.2.4. Calculer l'augmentation d'énergie cinétique de ce proton entre les armatures A et B. Comparer avec l'énergie attendue dans le ½mv12-½mv02 =0,5 x1,7 10-27[ (3,5 105)2-4 106)] ~1,04 10-16 J soit 1,04 10-16 / (1,6 10-19) ~6,5 102 eV. Le LHC est constitué d'un anneau de 27 km de circonférence. Le proton effectue plusieurs tours dans l'anneau. 1.3.1 Ce dispositif peut-il fonctionner avec des neutrons ? Non, le neutron ne possède pas de charge électrique. 1.3.2. Que faut-il modifier si l'on souhaite accélérer un électron ? L'électron possède une charge q = -e. Il faut donc changer le sens du champ électrique E, c'est à dire appliquer une tension opposée à la précédente entre les armatures A et B. ... .... 2. Collision entre deux protons. Deux faisceaux de protons ayant la même énergie cinétique se percutent de manière frontale en des points où sont placés de gigantesques détecteurs. 2.1. Faire un schéma illustrant la situation avant la collision entre deux protons en représentant leur vecteur vitesse. 2.2. Le système étudié, dans le référentiel terrestre, est constitué de l'ensemble des deux protons. Déterminer le vecteur quantité de mouvement du système avant collision. 2.3.On considère que le système est isolé. Choisir, parmi les trois schémas ci-dessous, celui qui correspond à la situation après collision des protons. Justifier. 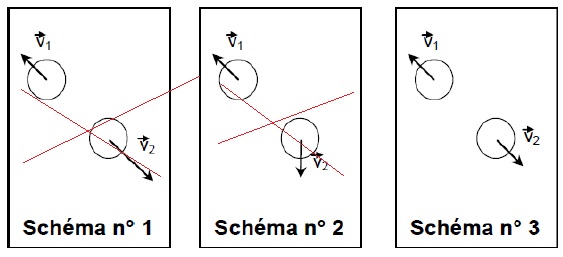Seul le schéma 3 convient. Le système étant isolé, le vecteur quantité de mouvement du système se conserve au cours du choc.

menu