Observation
des cratères lunaires, bac général 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
L'objectif
de cet exercice est de déterminer la cartéristique d'un oculaire d'une
lunette astronomique permettant d'observer des cratères lunaires depuis
la terre.
1. Etude de la lunette astronomique.
Fiche technique :
- distance focale objectif : 300 mm ; diamètre de l'objectif : 70 mm ;
masse : 1,95 kg ; hauteur réglable du trèpied 65 à 114 cm. Distance
focale des oculaires fournis : 35 mm ; 20 mm ; 10 mm.
1.1. Indiquer pourquoi cette lunette est commercialisée comme lunette " 70 / 300".
Le nom commercial précise " diamètre de l'objectif " suivi de " distance focale objectif".
1.2. La lunette est modélisée par deux lentilles minces convergentes. Le foyer image F ' obj de l'objectif coïncide avec le foyer objet Focu de l'oculaire. Compléter le schéma suivant.
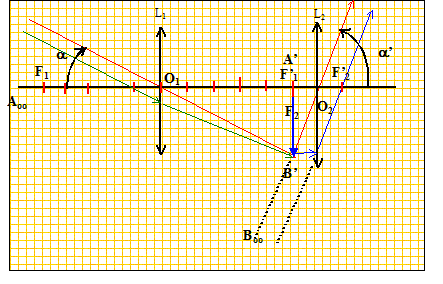1.3 Après avoir défini le terme "afocal", expliquer l'intérêt de disposer d'une lunette afocale.
Système afocal : l'image définitive est à l'infini.
Un oeil normal voit un objet sans
accommoder, sans fatigue, quand celui-ci est placé à
l'infini.
1.4. Définir le grossissement de la lunette et montrer que le grossissement a pour expression G = f 'obj / f 'ocu.
tan a =
A'B' / O1F'1 =
A'B' / f 'obj proche de a
radian si l'angle est petit.
tan a'
= A'B' / f 'ocu proche
de a'
radian si l'angle est petit.
G = a ' / a ; G = f 'obj / f 'ocu.
|
2. Observation d'un cratère lunaire.
2.1. Montrer que l'angle a sous lequel est vu le cratère lunaire depuis la terre a pour valeur 2,86 10-5 rad.
Distance terre -lune : D =3,84 105 km ; largeur du cratère : d = 11,0 km.
tan a ~a = d / D =11,0 / (3,84 105) =2,86 10-5 rad.
2.2. L'observation du cratère est-elle possible à l'oeil nu ?
Le pouvoir séparateur de l'oeil étant de 3,0 10-4 rad, le cratère ne peut pas être observé à l'oeil nu.
2.3. Dans ces conditions, calculer la taille de l'image intermédiaire A'B' du cratère à travers l'objectif de la lunette.
A'B' = f 'obj x a =300 x 2,86 10-5 =8,6 10-3 mm.
2.4. Quel(s) oculaire(s) faut-il utiliser ?
a' doit être supérieur ou égal à 3,0 10-4 rad.
A'B' / f 'ocu > 3,0 10-4 ; f 'ocu < A'B' / (3,0 10-4 ) ; f 'ocu < 8,6 10-3 / (3,0 10-4 ) ; f 'ocu < 28,6 mm.
Oculaires retenus : 20 mm ; 10 mm.
|
|