Mathématiques,
géométrie, logarithme, bac septembre 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Géométrie. 5 points
On considère le cube ABCDEFGH.
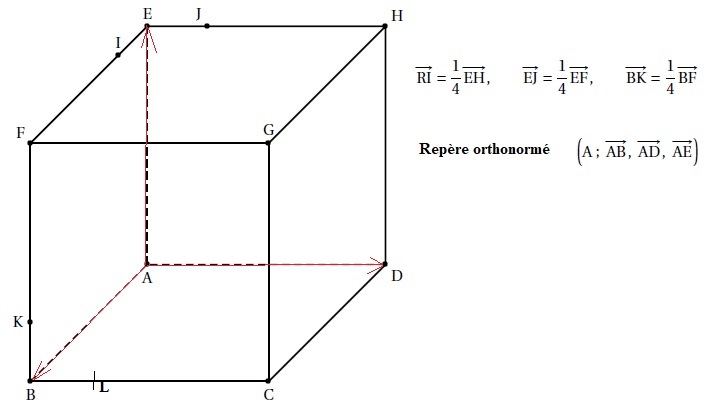
1. Donner sans justification les coordonnées des points I, J et K.
I(0,25 ; 0 ; 1) ; J( 0 ; 0,25 ; 1) ; K (1 ; 0 ; 0,25).
2. Démontrer que le vecteur suivant est normal au plan (IJK).

3. Montrer qu’une équation cartésienne du plan (IJK) est 4x +4y +4z −5 =0.
x +y +z +d = 0.
I(0,25 ; 0 ; 1) appartient à ce plan : 0,25 +0 +1 +d = 0 soit d = -1,25.
x+y+z-1,25 = 0 ou encore 4x +4y +4z −5 =0.
4. Déterminer une représentation paramétrique de la droite (BC).
Coordonnées d'un vecteur directeur de cette droite (0 ; 1 ; 0).
x = xB ; y = t+yB ; z = zB avec t réel.
x= 1 ; y = t ; z =0.
5. En déduire les coordonnées du point L, point d’intersection de la droite (BC) avec le plan (IJK).
4xL +4yL +4zL −5 =0 avec xL = 1 ; yL = t ; zL = 0.
4+4t-5=0 ; t = 0,25.
L( 1 ; 0,25 ; 0).
6. Sur la figure , placer le point L et construire l’intersection du plan (IJK) avec la face (BCGF).
7. Soit M ( 0,25 ; 1 ; 0). Montrer que les points I, J, L et M sont coplanaires.
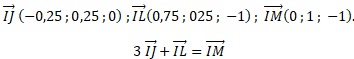
L'un des vecteurs étant une combinaison linéaire des deux autres, ces trois vecteurs sont coplanaires.
|
...
|
....
|
Logarithme (5 points).
Partie 1.
On considère la fonction h définie sur l’intervalle ]0 ; +∞[ par :
h(x) =1+ ln(x) / x.
1. Déterminer la limite de la fonction h en 0.
ln(x) tend vers moins l'infini ; ln(x) tend vers moins linfini ainsi que h(x).
2. Déterminer la limite de la fonction h en +∞.
Par croissance comparée ln(x) / x tend vers zéro et h(x) tend vers 1.
3. On note h′ la fonction dérivée de h. Démontrer que, pour tout nombre réel x de ]0 ; +∞[,
on a : h′(x) = (1−ln(x)) / x2 .
on pose u = ln(x) et v = x ; u' = 1 /x et v' = 1.
(u'v-v'u) / v2 = (1-ln(x)) / x2.
4. Dresser le tableau de variations de la fonction h sur l’intervalle ]0 ; +∞[.
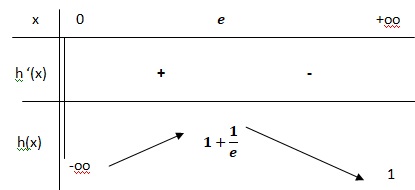
5. Démontrer que l’équation h(x)= 0 admet une unique solution α dans ]0 ; +∞[.
Justifier que l’on a : 0,5 < α < 0,6.
Sur [e ; +oo[, l'équation h(x) =0 n'admet pas de solution.
Sur ]0 ; e[, h(x) et continue et strictement croissante de -oo à 1+1 /e.
D'après le théorème de la bijection, h(x) = 0 admet une unique solution sur cet intervalle.
h(0,5) ~ -0,38 < 0 ; h(0,6) ~ 0,15 > 0.
Sur ]0 ; e[, h(x) et continue et strictement croissante, donc 0,5 < α < 0,6.
Partie II.
Dans cette partie, on considère les fonctions f et g définies sur ]0 ; +∞[ par :
f (x)= x ln(x)−x ; g(x) = ln(x).
On note Cf et Cg les courbes représentant respectivement les fonctions f et g dans un repère orthonormé.
Pout tout nombre réel a strictement positif, on appelle :
• Ta la tangente à Cf en son point d’abscisse a ;
• Da la tangente à Cg en son point d’abscisse a.
Les courbes Cf et Cg ainsi que deux tangentes Ta et Da sont représentées ci-dessous.
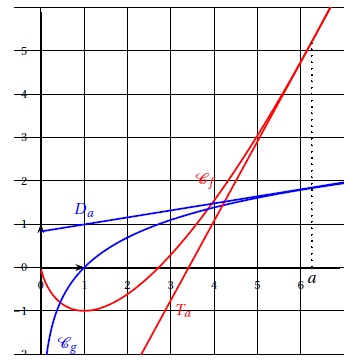
On recherche d’éventuelles valeurs de a pour lesquelles les droites Ta et Da sont perpendiculaires.
Soit a un nombre réel appartenant à l’intervalle ]0 ; +∞[.
1. Justifier que la droite Da a pour coefficient directeur 1 / a.
g'(x) = 1 /x ; g'(a) = 1 /a.
2. Justifier que la droite Ta a pour coefficient directeur ln(a).
On pose u = x et v = ln(x) ; u' = 1 ; v' = 1/x.
u'v+v'u =ln(x)+1.
f '(x) = ln(x) +1 -1 = ln(x) ; f '(a) = ln(a).
On rappelle que dans un repère orthonormé, deux droites de coefficients
directeurs respectifs m et m′sont perpendiculaires si et seulement si
mm′
= −1.
3. Démontrer qu’il existe une unique valeur de a, que l’on identifiera, pour laquelle les droites Ta et Da sont perpendiculaires.
Ta et Da étant perpendiculaires , ln(a) / a = -1 ; ln(a) / a+1 =0 soit h(a) = 0.
D'après la partie I, a = a.
|
|