Le baseball, bac S métropole 09 /2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . ...... ..... Lancer de la balle. L'objectif du lanceur est de lancer la balle avec la plus grande vitesse possible ( de l'ordre de vballe = 140 km / h. Les deux joueurs ( batteur et lanceur ) sont distants sur le terrain d'une distance d = 18,50 m. 1.1 Evaluer la durée mise par la balle pour arriver au batteur. 140  / 3,6 ~38,9 m /s ; 18,50 / 38,9 ~0,476 s. 1.2. Justifier la difficulté du batteur pour frapper à temps la balle lancée. Le cerveau humain traite l'image ( 0,10 s). Le cerveau commande les muscles (  0,13 s). La trajectoire sera t-elle droite ou courbe ? ( 0,13 s) Le batteur ne voit pas la balle sur la dernière partie de la trajectoire. Nous percevons les objets plus avancé qu'ils ne le sont en réalité. Lors des lancers, la valeur de la vitesse de la balle lancée est mesurée à l'aide d'un radar Doppler disposé derrière le batteur. Ce dispositif émet des ondes de fréquence f = 10,252 GHz. Ces ondes réfléchies par la balle sont détectées par la balle. La valeur f ' de leur fréquence est alors mesurée. 1.3.  f ' est-elle supérieure, inférieure ou égale à f. Justifier. La balle s'éloigne de l'émetteur. f ' < f. 1.4. Dans la situation étudiée, plusieurs expressions sont proposées. En justifiant, indiquer, pour chaque proposition, si elle est correcte ou non. f ' = f (1 +2v / c). Faux, car f ' est supérieure à f. f ' = f ( 1-2v / c). Vrai, car f ' est inférieure à f. f ' = f ( c+2v). Faux, le premier membre est homogène à une fréquence et le second à une fréquence fois une vitesse. 1.5. Expliquer qualitativement l'origine du facteur 2 dans l'expression retenue. L'émetteur - récepteur est fixe ; la balle s'éloigne de celui-ci. L'onde se réfléchi sur la balle et revient vers l'émetteur : il y a un double effet Doppler. 1.6. Evaluer la valeur de la différence f ' - f mesurée par le radar dans le cas d'une balle lancée par un joueur professionnel. f ' - f = -2v f / c = -2 x 38,9 x10,252 109 / (3 108) ~ -2,7 kHz. Vitesse de la balle battée. Lors du choc, la balle se déforme et une partie de son énergie mécanique est dissipée. On souhaite connaître le coefficient de restitution e de cette balle. e = Vaprès / Vavant. Une balle de baseball sans vitesse initiale est lâchée d'une hauteur initiale h1 au dessus du sol. On néglige les actions de l'air. Graphique représentant l'altitude de la balle au cours des rebonds successifs. 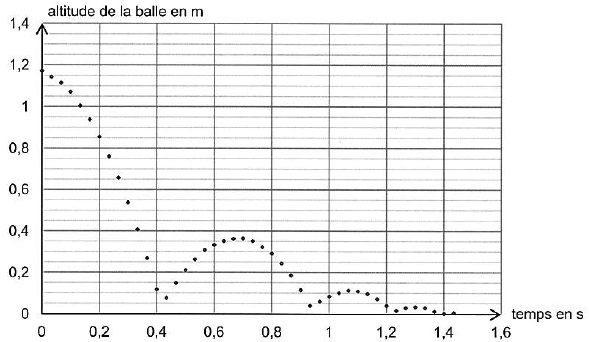2.1. Rappeler les expressions des énergies cinétique et potentielle de pesanteur. On note m ( kg)  la masse de la balle. Energie cinétique ( joule) = ½mv2 avec v vitesse de la balle ( m /s). Energie potentielle de pesanteur (joule) = m g z . g = 9,8 m s-2 et z altitude en m, l'origine étant le sol. 2.2. En justifiant la conservation de l'énergie mécanique, exprimer en fonction de h1, l'énergie cinétique de la balle juste avant son premier impact au sol. La balle n'est soumise qu'à son poids, les frottements étant négligés. L'énergie mécanique se conserve lors de la chute. Initialement, l'énergie mécanique est sous forme potentielle de pesanteur : mgh1 . Juste avant le sol, l'énergie mécanique est sous forme cinétique :  ½mv2avant . L'énergie mécanique se conserve : mgh1 =½mv2avant . 2.3 On note h2 la plus haute hauteur atteinte par la balle après un premier rebond. Montrer que e = (h2 / h1)½. Lorsque la hauteur maxi est atteinte, l'énergie mécanique est sous forme potentielle de pesanteur : mgh2 . Juste après le rebond, l'énergie mécanique est sous forme cinétique :  ½mv2après . L'énergie mécanique se conserve : mgh2 =½mv2après . e = Vaprès / Vavant= (h2 / h1)½. 2.4. Evaluer le coefficient de restitution de la balle. D'après le graphe : h1 ~1,15 m ; h2 ~0,35 m ; e ~(0,35 / 1,15)½ ~0,55. 2.4. La vitesse v0 de la balle battée dépend de la vitesse de la balle vballe juste avant qu'elle soit frappée et de la vitesse V que le batteur communique à la balle au point d'impact : v0=(1+q) V + q vballe. q est déterminé notamment à l'aide du coefficient e. V est de l'ordre de 110 km / h ; q = 0,25. 2.5 Calculer en km / h la valeur de la vitesse de la balle battée et commenter. v0= (1+0,25)x110 +0,25 x140 ~1,8 102 km / h. Cette vitesse est grande, le batteur aura le temps d'atteindre l'une des bases du terrain. ... .... 3. Portée de la balle battée. Après la frappe de balle par le batteur, la balle est envoyée vers le fond du terrain. L'analyse des images de la frappe permettent de mesurer la valeur v0 de la vitesse de la balle battée et l'angle de frappe a. Une étude numérique permet de prévoir la durée du vol et la portée de la balle. On souhaite confronter les prédictions avec l'étude simplifiée du mouvement de la balle après la frappe dans le référentiel terrestre du terrain, supposé galiléen. Les actions de l'air sur la balle sont négligeables. L'origine O du référentiel correspond à la position initiale de la balle battée. 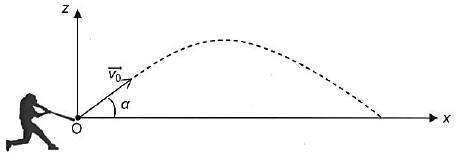On donne v0 = 182 km / h ; a = 19 ° ; durée de vol prévue 4,5 s ; portée prévue 117 m. 3.1. Effectuer le billan des forces qui s'exercent sur la balle ( de masse m) après la frappe. La balle n'est soumise qu'à son poids P = mg. 3.2. A l'aide d'une loi de Newton à énoncer, établir les équations horaires du mouvement x(t) et z(t). Seconde loi de Newton : dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées au système est égale au produit de la masse du solide par l'accélération de son centre d'inertie G. Composante du vecteur accélération : ( 0 ; -g). Composante du vecteur vitesse, primitive du vecteur accélération :  v0 cos a ; -gt + v0 sin a. Composante du vecteur position, primitive du vecteur vitesse. x(t) = v0 cos a t ; z(t) = -½gt2 + v0 sin a t . 3.3. Montrer que la trajectoire de la balle vérifie l'équation : z(x) = -½g x2 / (v0 cos a)2 +x tan a. t = x(t) /( v0 cos a ). Repport dans z(t) puis simplifier. z(t) = -½g(x(t) /( v0 cos a ) )2 + v0 sin a ( x(t) /( v0 cos a )). 3.4 Calculer la portée de la balle dans le cas de ce modèle simplifié. Au sol z(x) = 0. -½g x2 / (v0 cos a)2 +x tan a=0 ; La solution x = 0 correspond à la position initiale. -½g x / (v0 cos a)2 + tan a=0 ; -½g x / (v20 cos a) + sin a=0 ; x=2 v20 sin a cos a / g = v20 sin (2a ) / g. v0 = 182 / 3,6 = 50,55 m /s ; x = 50,552 x sin (38) / 9,8 ~161 m. 3.5. Comparer la valeur calculée avec la valeur prévue et commenter. La valeur calculée est bien supérieure à la valeur prévue. Le modèle simplifié n'est pas valide, il faut prendre en compte les frottements.   Rejoindre la première base. En attaque, le but du jeu est de frapper la balle puis de progresser de base en base pour retourner à la base de départ afin d'inscrire des points. Pour atteindre la première base, l'option la plus commune est de frapper la balle de sorte que sa durée de vol soit suffisamment longue pour que le batteur ait le temps de rejoindre la première base. Le batteur frappe la balle avec un angle de 40 °. Dans cette étude les actions de l'air sont négligées et un estimation de la valeur de la vitesse de course du joueur est attendue. Dans ces conditions, déterminer la vitesse minimale de la balle battée pour que le batteur puisse rejoindre la première base. Commenter la valeur obtenue en sachant que les frottements de l'air ont tendance à augmenter la durée du vol. 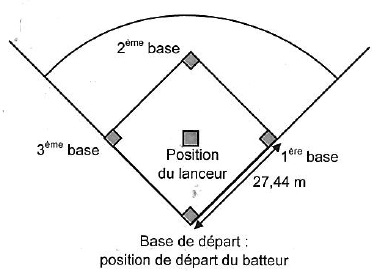Vitesse de course du batteur  : 30 km /h soit 30 / 3,6 ~8,3 m /s. Durée pour atteinde la première base : 27,44 / 8,3 ~ 3,3 s. Portée de la balle : x = v20 sin (2a ) / g = v20 sin (80 ) / 9,8 ~0,1 v20. Durée du vol de la balle : t = x(t) /( v0 cos a ) = 0,1 v20 / ( v0 cos(40)) =0,1 v0 / cos (40) ~0,13 v0. 0,13 v0 doit être supérieur à 3,3 ; v0 > 25 m / s ( 91 km / h). Le batteur a le temps d'atteindre la première base.

menu