Spécialité
mathématiques,
bac général 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
QCM ( 5 points ).
Une seule des 4 réponses
proposées est exacte.
1. On considère
les suites (un) et (vn) telles que, pour tout
entier naturel n :
un = 1-0,25n ; vn = 1+0,25n.
On considère de plus une suite (wn) qui, pour tout entier naturel n
vérifie un <
wn < vn.
On peut affirmer que :
a. Les suites (un)
et (vn) sont géométriques. Faux.
b. La suite (wn) converge
vers 1. Vrai.
0,25n
tend vers zéro quand n tend vers l'infini et vn,
ainsi que un tendent vers 1.
c.
La suite (un) est minorée par 1. Faux.
La suite (un)
est majorée par 1.
d.
La suite (wn) est croissante. Faux.
2.
On considère la fonction f définie sur R par f(x) = x exp(x2).
a. f '(x) =2x exp(x2).
On pose u = x et v = exp(x2)
; u' = 1 ; v' = 2x exp(x2).
u'v +v'u =exp(x2) +2x2 exp(x2)=
(2x2
+1)exp(x2).
b. f '(x)
=(1+2x)exp(x2).
c.
f '(x) =(1+2x2)exp(x2). Vrai.
d.
f '(x) =(2+x2)exp(x2).
3.
Que vaut la limite de (x2-1) / (2x2 -2x+1)
quand x tend vers plus l'infini ?
-1 ; 0 ; 0,5 vrai ; +oo.
Mettre x2
en facteur commun au numérateur et au dénominateur.
x2 (1-1 /x2) / (x2(2-2 /x +1/x2)).
Simplifier : (1-1 /x2) / (2-2 /x
+1/x2).
1 / x et 1 /x2 tendent vers zéron si x tend vers plus
l'infini.
4. On considère
une fonction h continue sur l'intervalle [-1 ; 1 ] telle que :
h(-1) =0 ; h(0) = 2 ; h(1) = 0.
On peut affirmer que :
a. La fonction h
est croissante sur l'intervalle [-1 ; 0].
b. La fonction h est positive sur
l'intervalle [-1 ; 1].
c. Il existe au moins un nombre réel
a dans l'intervalle [0 ; 1] telle que h(a) = 1. Vrai.
d. L'équation h(x)
=1 admet exactement 2 solutions dans l'intervalle [-1 ; 1].
5. On suppose que g
est une fonction dérivable sur l'intervalle [-4 : 4 ]. On donne
ci-dessous la représentation graphique de sa fonction dérivée g'(x).
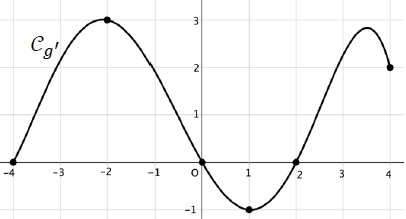
On peut affirmer que :
a. g admet un
maximum en -2. Faux, g'(x) n'est pas
nulle en x = -2.
b. g est croissante
sur l'intervalle [1 ; 2]. Faux, g'(x)
est négative sur cet intervalle.
c. g est convexe
sur l'intervalle [1 ; 2]. Vrai
; g'(x) est croissante sur [1 ; 2]
d. g admet un
minimum en zéro. Faux; g'(0)=0 ;
g'(x) >0 , g(x) croissante sur [-4
; 0] et g'(x)négative donc g(x) décroissante
sur [0 ; 2].
Il s'agit donc d'un
maximum.
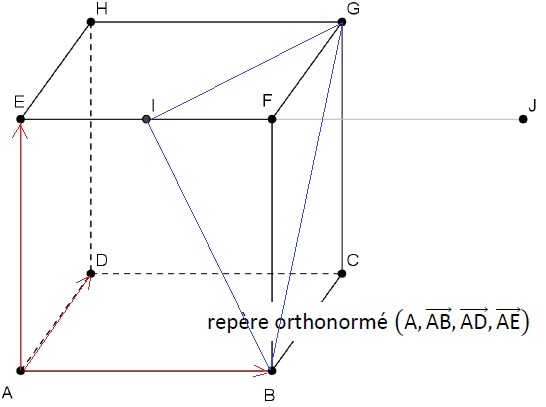
Exercice 2. 5 points.
On considère le cube ABCDEFGH de côté 1, le milieu I de (EF] et J le
symétrique de E par rapport à F.
1.a. Par lecture graphique, donner
les coordonnées des points I et J.
I(0,5 ; 0 ; 1) ; J(2 ; 0 ; 1).
b. En déduire les
coordonnées des vecteurs 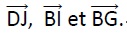 . .
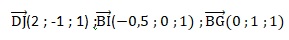
c. Montrer que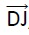 est un vecteur normal au plan(BGI). est un vecteur normal au plan(BGI).
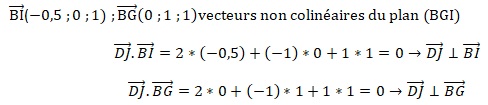
d. Montrer qu'une
équation cartésienne du plan (BGI) est 2x-y+z-2=0.
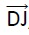 est un vecteur normal au plan(BGI) : 2x -y+z+d=0. est un vecteur normal au plan(BGI) : 2x -y+z+d=0.
B(1 ; 0 ; 0) appartient à ce plan : 2*1-0+0+d=0 ; d = -2.
2. On note d la droite passant par F
(1 ; 0 ; 1) et orthogonale au plan (BGI).
a. Déterminer une
représentation paramétrique de la droite d.
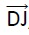 est un vecteur directeur de la droite d. est un vecteur directeur de la droite d.
Equation paramétrique de la droite d : x = 2t+xF =2t +1.
y = -t+yF = -t.
z = t+zF = t+1 avec t réel.
b. On considère le
point L de coordonnées (2 /3 ; 1 /6 ; 5 /6).
Montrer que L est le point d'intersection de la droite d et du plan
(BGI).
Hypothèse : L appartient à la droite d : 2t+1 =2 /3 ; t = -1 / 6.
yL = -(-1/6) = 1 /6 ; zL = -1 /6 +1 = 5 /6. L'hypothèse est vraie.
Si L appartient au plan (BGI) :
2xL-yL+zL-2=0 ; 4 /3 -1 /6 +5 /6-2 =(8-1+5-12) / 6 =0 est bien vérifié.
Donc L est le point d'intersection de la droite d et du plan
(BGI).
3.a Calculer le
volume de la pyramide FBGI. ( V = B h / 3 avec B aire de base et h sa
hauteur).
Base : triangle BFG d'aire FG *Fb / 2 = 1 *1 / 2 = 0,5.
Hauteur : FI =0,5.
Volume de cette pyramide : 0,5 *0,5 / 3 = 0,25 / 3 = 1 /12.
b. En déduire
l'aire du triangle BGI.
Base de la pyramide : triangle BGI ; hauteur FL.
FL2 =(2 /3-1)2 +(1 / 6-0)2 +(5/6-1)2=1 / 9 +1 /36 +1/ 36=6 /36 = 1 /6.
FL = 1 /6½.
Aire du triangle BGI = 3 Volume de la pyramide FBGI / FL =1 /4 *6½ =6½ / 4.
|
|
|
|
Exercice 3. ( 5
points).
Pour préparer l'examen du permis de conduire on distingue deux types de formation :
- Formation avec conduite accompagnée.
- Formation traditionnelle.
On considère un groupe de 300 personnes venant de réussir cet examen. Dans ce groupe :
-
75 personnes ont suivi une formation avec conduite accompagnée ; parmi
elles, 50 ont réussi l'examen à leur première présentation et les
autres à leur seconde présentation.
- 225 personnes ont suivi une formation traditionnelle ; parmi elles, 100 ont réussi l'examen à leur
première présentation, 75 à leur seconde présentation et 50 à la troisième présentation. On interroge au hasard une personne de ce groupe. On considère les événements :
A : la personne a suivi la formation avec conduite accompagnée.
R1 : réussite à la première présentation.
R2 : réussite à la seconde présentation.
R3 : réussite à la troisième présentation.
1. Modéliser la situation par un arbre pondéré.
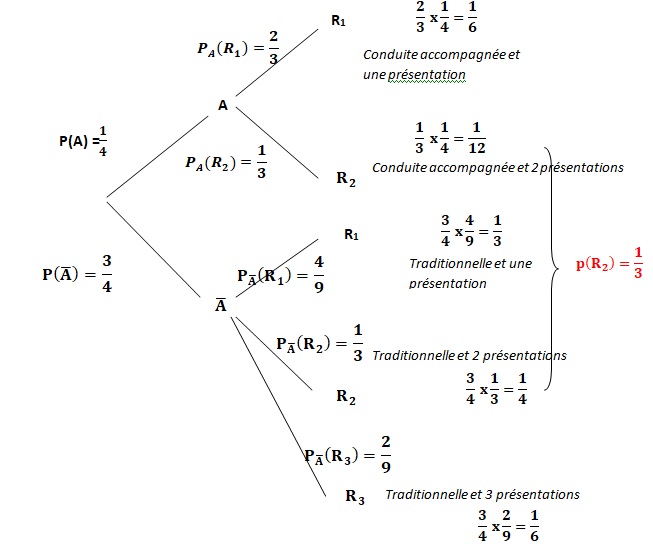
2.a
Calculer la probabilité que la personne interrogée ait suivi une
formation avec conduite accompagnée et réussi l'examen à sa deuxième
présentation. 1 /12 ( voir ci-dessus).
2.b. Montrer que la
probabilité que la personne interrogée ait réussi l'examen à sa
deuxième présentation est égale à 1 /3. ( Voir ci-dessus).
2.c. La personne
interrogée a réussi l'examen à sa seconde présentation. Quelle est la
probabilité qu'elle ait suivi une formation avec conduite accompagnée ?
PR2(A) =P(A n R2 ) / P(R2) =1 / 12 / (1 /3) = 3 /12 = 1/ 4 =0,25.
3.
On note X la variable aléatoire qui, à toute personne choisie au hasard
dans le groupe, associe le nombre de fois où elle s'est présentée à
l'examen jusqu'à sa réussite.
a. Déterminer la loi de probabilité de X.
X
|
1
|
2
|
3
|
Probabilité
|
1 /6 + 1 /3 = 0,5
|
1 / 3
|
1 / 6
|
Soit A le point de
coordonnées (-0,5 ; 3).
b. Calculer l'espérance de cette variable et interpréter.
E =0,5 +2 /3 +3 / 6 =3 /6 +4 /6 +3/6 =10 /6 = 5 / 3~1,67.
En moyenne, les candidats se présentent 1,67 fois à l'examen avant de réussir.
4. On choisit,
successivement et de façon indépendante, n personnes parmi les 300 du
groupe, où n est un entier naturel non nul. On assimile ce choix à un
tirage avec remise de n personnes parmi les 300. On admet que la
probabilité de l'événement R3 est 1 / 6.
a. Préciser un événement dont la probabilité est égale à 1-(5 /6)n.
Probabilité qu'une personne réussisse l'examen à la première ou à la deuxème présentation : 5 / 6.
Probabilité que n personnes réussissent l'examen à la première ou à la deuxème présentation : ( 5 / 6 )n.
Probabilité qu'au moins une personne parmi n personnes choisies réussissent l'examen à la troisième présentation : 1-(5 /6)n.
On considère la fonction Python seuil ci-dessous, où p est un nombre réel appartenant à ]0 ; 1 [.
def seuil(p)
n=1
while 1-(5 / 6)**n <=p
n = n+1
return n
b. Quelle est la valeur renvoyée par la commande seuil(0,9) ? interpréter.
1-(5 /6)n < 0,9 ; (5 /6)n > 0,1 ; n ln(5 /6) > ln(0,1) ; n < 12,6 soit 13.
Il faut interroger 13 personnes pour que la probabilité qu'au moins
l'une d'entre elles ait réussi l'examen lors du troisième passage soit
strictement supérieure à 0,9.
|
Traiter l'exercice A ou l'exercice B.
Exercice A. ( 5 points)
Sur le graphique ci-dessous, on a représenté dans un repère orthonormé :
- la courbe Cf repésentative de le fonction f définie et dérivable sur ]0 ; +oo[ ;
- la tangente TA à la courbe Cf au point A de coordonnées (1 /e ; e) ;
- la tangente TB à la courbe Cf au point B de coordonnées (1 ; 2).
TA est parallèle à l'axe des abscisses. TB coupe l'axe des abscisses au point de coordonnées (0 ; 3).
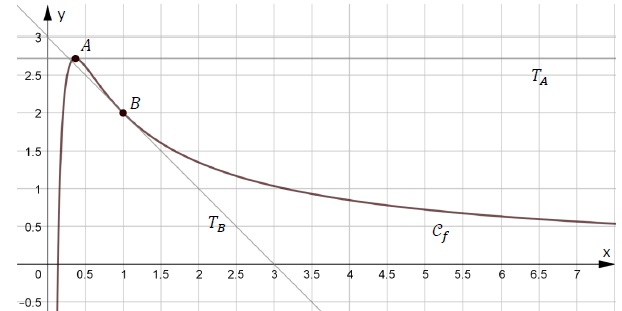
On note f ' la fonction dérivée de f.
Partie I.
1. Déterminer graphiquement les valeurs de f '(1 /e) et de f '(1).
f '(1/e) : coefficient directeur de la tangente TA, parallèle à l'axe des abscisses : f '(1/e) = 0.
f '(1) = -3 / 3 = -1 coefficient directeur de la tangente TB.
2. En déduire une équation de la tangente TB.
y = -x+b, TB passe au point de coordonnées (3 ; 0) ; 0 = -3+b ; b = 3. y = -x+3.
Partie II. On suppose que f(x) = (2+ln(x) / x.
1. Par le calcul, montrer que la courbe Cf passe par les points A et B et qu'elle coupe l'axe des abscisses en un point unique à préciser.
f(1 /e) =(2+ln(1/e) / (1 /e) = e (2-ln(e)) = e (2-1) =e = yA.
f(1) =(2+ln(1) / 1 =(2+0) /1 = 2 =yB.
(2+ln(x) / x =0 ; 2 +ln(x) = 0 ; ln(x) = -2 ; x = e-2.
2. Déterminer la limite de f(x) en 0+ et en plus l'infini.
En plus l'infini 2 / x tend vers zéro et par croissance comparée ln(x) / x tend vers zéro : f(x) tend vers zéro.
En 0+, ln(x) tend vers moins l'infini et 1 / x tend vers +oo : f(x) tend vers moins l'infini.
3. Montrer que f '(x) = (-1-ln(x)) / x2.
On pose u = 2+ln(x) et v = x ; u' = 1 /x et v' = 1.
(u'v-v'u) / v2 =(1-(2+ln(x) / x2 =(-1-ln(x)) / x2.
4. Dresser le tableau de variation de f.
f '(x) = 0 si x = 1 /e.
f '(x) négative sur ]0 : 1 /e] et f(x) est croissante.
f '(x) positive sur ]1 /e : +oo[ et f(x) est décroissante.
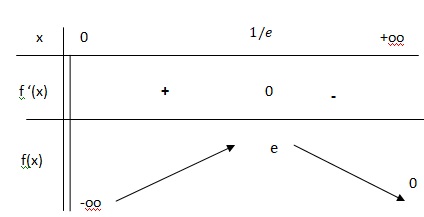
5. On admet que la dérivée seconde de f est f "(x) =(1+2ln(x)) / x3. Déterminer le plus grand intervalle sur lequel f est convexe.
La dérivée seconde doit être positive.
(1+2ln(x)) / x3 > 0 avec x appartenant à ]0 ; +oo[.
1+2ln(x) > 0 ; ln(x) > -0,5 ; x > e-0,5.
|
Exercice B.
Dans une boulangerie, les baguettes sortent du four à 225°C. On
s'intéresse à l'évolution de la température d'une baguette après sa
sortie du four.
On peut modéliser cette évolution à l'aide d'une fonction f définie et
dérivable sur [0 ; +oo[. f(t) représente la température en °C de la
baguette au bout de la durée t, exprimée en heure, après la sortie du
four. La température de la boulangerie est 25°C.
f est solution de l'équation différentielle y'+6y=150.
1.a Préciser f(0). f(0) =225.
b. Résoudre l'équation différentielle.
Solution générale de y' +6y =0 : y =A e-6t avec A une constante.
Solution particulière de y'+6y=150 : y = 25°C, température de la boulangerie.
Solution générale de y'+6y=150 : f (t) = A e-6t +25.
f(0) = 225 =A +25 ; A = 200.
f(t) = 200 e-6t+25.
2. Par expérience,
on observe que la température d'une baguette sortant du four décroît et
tend à se stabiliser à température ambiante.
La fonction f fournit-elle un modèle en accord avec ces observations.
Quand t tens vers plus l'infini, e-6t tend vers zéro et f(t) tend vers 25, température ambiante.
f '(t) =-1200e-6t négative, f(t) est strictement décroissante.
La fonction f est en accord avec ces observations.
3. Montrer que f(t) = 40 admet une unique solution sur [0 ; +oo[.
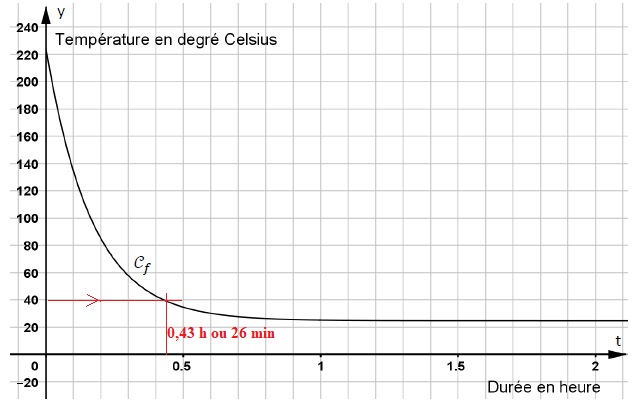
200e-6t+25=40 ; e-6t = 15 / 200 =0,075 ; 6t = - ln(0,075) ; t = -ln(0,075) / 6 ~0,43 heure ou 26 minutes.
Pour mettre les baguettes en rayon, le boulanger attend que leur température soit inférieure ou égale à 40°C. On note T0 le temps d'attente minimal entre la sortie du four et la mise en rayon.
4. Déterminer graphiquement T0.
5. On s'intéresse àla diminution, minute par minute, de la température d'une bagette à la sortie du four.
Dn désigne la diminution de la température en °C d'une baguette entre la n-ième et la (n+1)-ième minute après sa sortie.
Dn= f (n /60) -f((n+1) /60).
a. Vérifier que 19 est une valeur approchée de D0 et interpréter.
D0= f (0) -f(1) /60) = 225-(200e-0,1+25)~19.
Lors de la première minute, la température de la baguette diminue de 19°C.
b. Vérifier que Dn = 200e-0,1n(1-e-0,1). En déduire le sens de variation de la suite puis sa limite.
Dn =200[e-0,1n+25-(e-0,1(n+1)+25))=200 [e-0,1n-e-0,1(n+1)]=200 [e-0,1n-e-0,1n e-0,1]=200e-0,1n(1-e-0,1).
200e-0,1nest positif ; 1- e-0,1>0 ; Dn>0 ; f (n /60) > f((n+1) /60).
La suite est décroissante.
Quand n tend vers plus l'infini, e-0,1n tend vers zéro ; la température de la baguette de varie plus. Celle-ci a la température ambiante.
|
|


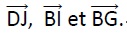
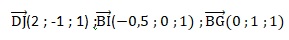
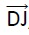 est un vecteur normal au plan(BGI).
est un vecteur normal au plan(BGI).